20. Понятие отношения

В математике изучают не только сам^объекты (числа, фигуры, величины), но и связи, отношения между ними. Так, усвоение понятия натурального числа — одного из ведущих понятий началь­ной математики и математики вообще — происходит благодаря изучению различных взаимосвязей между числами. Например, выясняется, что:

число 5 больше числа 2;

число 10 больше числа 8 на 2;

число 7 следует за числом 6, т. е. числа связаны различными отношениями: «больше», «больше на», «следует за» и др.

В геометрии изучают параллельность и перпендикулярность прямых, равенство и подобие фигур, т. е. различные отношения между геометрическими объектами.

Сравнивая множества, мы говорим, например, что они пере­секаются, или равны, или одно включено в другое, т. е. устанавли­ваем отношения между множествами.

В математике чаще всего рассматривают отношения между двумя объектами. Их называют бинарными. В нашем курсе мы будем изучать только такие отношения, поэтому в дальнейшем слово «бинарные» будем опускать.

Перед нами стоит задача: имея представления о конкретных отношениях между числами, геометрическими фигурами, множества­ми и другими объектами, установить, что общего у этих отношений, каким образом можно классифицировать такое огромное число самых разнообразных отношений. Знание этого материала нужно учителю начальных классов для того, чтобы, изучая конкретные отношения в начальной школе, понимать их общность, взаимосвязи, роль в усвоении тех или иных понятий.

Выясним сначала, что общего у различных известных нам отношений.

Рассмотрим множество чисел ^={3, 4, 5, 6, 8). Между числами этого можества существует отношение «больше»: 4>3. 5>3, 6>3, 8>3, 5>4, 6>4, 8>4, 6>5, 8>5, 8>6.

Можно рассмотреть для данных чисел и отношение «больше на 1»: «4 больше 3 на 1», «5 больше 4 на 1», «6 больше 5 на 1».

Числа данного множества связаны также отношением «меньше в 2 раза»: «3 меньше 6 в 2 раза», «4 меньше 8 в 2 раза».

Можно указать и другие отношения между числами 3, 4, 5, б и 8, мы ограничимся тремя, названными выше.

Обратим внимание на следующее: рассматривая то или иное отношение, мы каждый раз оперировали упорядоченными парами, образованными из чисел данного множества. Для отношения «боль­ше» это было множество {(4, 3), (5, 3), (6, 3), (8, 3), (5, 4), (б, 4), (8, 4), (6, 5), (8, 5), (8, б)), для отношения «больше на 1» — {(4, 3),

(5, 4), (6, 5)}, а для отношения «меньше в 2 раза» — множество, содержащее две пары: {(3, 6), (4, 8)}. Таким образом, можно сказать, что каждое из рассматриваемых отношений определяется множест­вом пар чисел, образованных из элементов множества Х = {3, 4, 5, 6, 8}.

Известно, что упорядоченные пары — это элементы декартова произведения множеств или его подмножеств. Нетрудно видеть, что те множества пар, которые определяют отношения «больше», «больше на 1» и «меньше в 2 раза», являются подмножествами декартова произведения ХХХ = {(3, 3), (3, 4), (3, 5), (3, 6), (3, 8), (4, 3), (4, 4), (4, 5), (4, 6), (4, 8), (5, 3), (5, 4), (5, 5), (5, 6), (5, 8), (6, 3), (6, 4). (6, 5), (6. 6), (6, 8), (8, 3), (8, 4), (8, 5), (8, 6), (8. 8)).

Итак, каждое из рассматриваемых отношений определяется множеством пар, которое, в свою очередь является подмножеством декартова произведения XXX.

Вместо того чтобы говорить, что отношение определяется мно­жеством пар, в математике само это множество пар называют отношением между элементами множества X.

Определение. Отношением между элементами множества X или отношением на множестве X называется всякое подмножество декартова произведения XXX.

Отношения обозначают прописными буквами латинского алфа­вита: Р, С?, Р, 5 и др. Следовательно, если Р — отношение между элементами множества X, то РаХХХ.

Отношения на конечном множестве X можно представлять на­глядно, при помощи особых чертежей, состоящих из точек, соединен­ных стрелками. Такие чертежи называют графами¹.

Построим, например, граф отношения «больше» между элементами множества Х = (2, 4, 6, 8, 12). Для этого элементы данного множества изобразим точками и соединим стрелками те точки, которые изображают числа, находящиеся в отноше­нии «больше». Поскольку 4 >2, то прово­дим стрелку от 4 к 2; так как 6 >4, то проводим стрелку от 6 к 4 и т. д., пока не переберем все пары чисел, связанных за­данным отношением. В результате получаем граф отношения «больше» для элемен­тов множества Х = [2, 4, 6, 8, 12} (рис. 56).

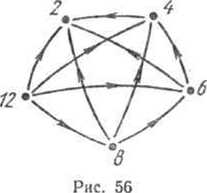
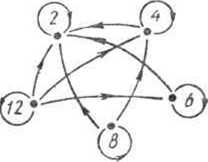
Рассмотрим теперь на том же множестве X отношение «кратно» и построим его граф.

¹ Слово «граф», так же как и слово «график», проис­ходит от греческого слова «графо» — пишу.

Аналогично предыдущему случаю изобразим элементы множества X точками и соединим стрелками те, которые изображают числа, находящиеся в отношении «кратно»: 12

кратно 2, 12 кратно 4 и т. д. Так как любое число из множества X кратно самому себе, то граф даного отношения будет иметь стрелки, начало и конец которых совпадут (рис. 57). Такие стрелки на графе называют петлями.

Упражнения

1. Приведите примеры отношений, существующих между:

1. натуральными числами; 2) прямыми на плоскости; 3) тре­угольниками; 4) множествами.

2. Из элементов множества Х = {0, 3, 6, 9, 12, 15, 18) образуйте всевозможные пары чисел так, чтобы компоненты пары (х, у) были связаны отношением:

1. «х больше у в 3 раза»; 2) «х больше у на 3». Постройте графы данных отношений.

3. Какое из следующих множеств является отношением между элементами множества Л={0, 3, 6, 9, 12):

1. Р = {(6, 3), (9, 3), (12, 3), (12, 6), (3. 3), (6, 6), (9, 9), (12, 12));

2. Т = ((3, 3), (3. 6), (3, 9), (3, 12), (6, 6), (9, 9), (12, 12));

3. М = ((3, 6), (6, 12), (9, 18))?

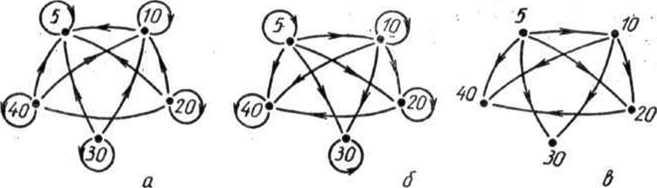
4. Установите, какой из графов, приведенных на рисунке 58, является графом отношения «х — делитель числа у», заданного на множестве В = (5, 10, 20, 30, 40).

5. На множестве Я = {0, 2, 4, 6, 8) заданы отношения Р, (?, 5. Постройте их графы, если:

Р — отношение «меньше»;

С? — отношение «меньше в 2 раза»;

5 — отношение «меньше на 2».

6. Множество М членов семьи Волковых состоит из отца Михайла Петровича, матери Веры Ивановны и детей: Толи, Кати, Пети и Оли. Между членами семьи существуют различные отноше­ния родства. Постройте графы отношений: 1) «быть дочерью»;

2. «быть братом»; 3) «быть матерью».

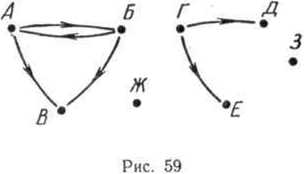
7. На рисунке 59 дан граф отно­шений «быть братом» на множестве детей, живущих в одном доме (де­ти обозначены точками А, Б, В, Г,

Д, Е, Ж, 3). Кто из них явля­ется девочкой, а кто мальчиком? О ком из ребят по этому графу нельзя ничего сказать?