§ 3. Математические доказательства 35

13. Дедуктивные рассуждения 35

14. Простейшие схемы дедуктивных рассуждений 41

15. Неполная индукция ’³ 44

16. Способы доказательства истинности высказываний 47

§ 4. Текстовые задачи и их решение 51

17. Понятие текстовой задачи 51

18. Способы решения текстовых задач 53

111111111111111111111III1111 ^>мъ° 56

(л п пс=л п(в п с). (Л1)В)ис=Л11(вис). 79

2) С=((а, (Ь, <Г), (а, с)); 96

□ □ □ о о о о 137

"^{еотрииатель}' ОООООКН8В2 145

«О О О О 141

^□□□□□□000 «О О О О О О 139

□ □□□□□□□□□□□ 158

& . 226

I „ 295

5. Даны множества Л = (а, 6) и В = (с, </}• Является ли множество С декартовым произведением множеств Л и В, если:

1. С = ((а, с), (а. О), (Ь. с). (Ь, </)};

2. С=((а, (Ь, <Г), (а, с));

3. С=((а, сО, (Ь. О), (с. с1), (а, с))?

6. Запишите различные двузначные числа, используя цифры 1, 2, 3, 4. Сколько среди них таких, запись которых начинается

с цифры 3?

Переформулируйте эту задачу, используя понятие декартова произведения множеств.

7. Запишите с помощью прямоугольной таблицы множества ЛХВ и ВхЛ, если Л = (1, 3, 5, 7}, В = {0, 2, 4, 6, 8). Сколько элементов содержат полученные декартовы произведения? Мож­но ли утверждать, что ЛХВ = ВХЛ?

8. Даны множества Х = (1. 2, 3, 4. 5} и У = {0, 4, 6, 8|. В каком из следующих случаев истинно высказывание Лег XX У, если:

1. Л ={(1, 4), (2. 4), (3, 4), (5, 4));

2. Л =((2, 0), (2, 6). (0, 6), (4, 4)};

3. Л={(3, 4), (4, 3), (5. 4), (3, 6))?

9. Проверьте справедливость равенства (Л Ч В) X С = = (ЛХС)ЩВХС) для множеств Л = {3, 5, 7); В = {6, 8, 9}, С = {0, 1}.

10. Выполняется ли для множества Л = (3, 5, 7, 8, 9}, В = (8, 9}, С = {0, I, 2} равенство (Л\В)ХС = (Л ХС)\(ВХС)?

11. Сколько букв в слове сбарабан»? Сколько различных букв в этом слове?

Переформулируйте эту задачу, используя понятия множества и кортежа.

12. Чем отличается множество цифр в записи числа 56 576 от кортежа цифр в его записи?

13. С помощью цифр 1, 2, 3 запишите всевозможные трехзнач­ные числа. Сколько таких чисел получилось?

20. Изображение декартова произведения двух числовых

множеств на координатной плоскости

Когда множества А и В конечны и содержат небольшое число элементов, найти их декартово произведение несложно. Л если множества А и В бесконечны? Как представить, например, декартово произведение множества А натуральных чисел, больших 3, и мно­жества В натуральных чисел, больших 5?

Круги Эйлера в этом случае нам помочь не могут.

В математике нашли выход из этой ситуации. Оказывается, наглядное изображение декартова произведения двух числовых мно­жеств можно получить при помощи координатной плоскости. Каким образом?

Чтобы ответить на этот вопрос, уточним наши представления о координатной прямой и координатной плоскости.

Координатная прямая — это прямая с заданным на ней началом отсчета, единицей длины и положительным направлением (рис. 46).

Каково назначение координатной прямой?

Возьмем на прямой I точку М (М не совпадает с О) и поставим ей в соответствие такое число х, что:

1. его модуль равен расстоянию от О до М;

2. оно положительно, если точка М лежит на луче ОЕ, и отри­цательно, когда точка М лежит на противоположном луче.

Так, определенное число х называют координатой точки М и пи­шут: М (х).

Например, на рисунке 47 точка М имеет координату 4, точка К — координату —2.

В том случае, когда точка М совпадает с точкой О, считают что координата точки М равна нулю, н пишут: Л1 (0).

Таким образом, с введением координатной прямой устанавлива­ется связь между точками прямой и действительными числами: каждой точке М координатной прямой соответствует единственное действительное число х — координата этой точки. Справедливо и обратное утверждение: каждое действительное число х сопоставляет-

М

Я

_1 1

О Е

О Е Рис. 46

ся единственной точке М, имеющей число х своей координатой.

С М

ТТ Те Г

Рис. 48

Например, число 7 на координат­ной прямой (рис. 48) можно изобра­зить точкой¹М (7), а число — 3,5 — точкой С ( — 3,5).

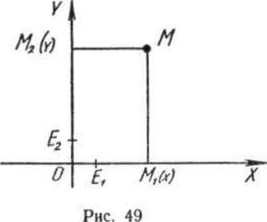
Возьмем две взаимно перпенди­кулярные координатные прямые Ох и Оу с общим началом и единицами длины ОЕ| и ОЕг, такими, что 0Е\ = = 0Е? (рис. 49). Такие прямые Ох и Оу называются осями пря­моугольной системы координат, при­чем прямую Ох называют осью абсцисс, а прямую Оу — осью орди­нат. Плоскость с построенными в ней осями координат, имеющими общее начало отсчета (точку пересечения этих прямых) и одну н ту же единицу длины, назы­вают координатной плоскостью.

Каково назначение координатной плоскости? Возьмем на коор­динатной плоскости точку М (рис 49). Ее положение здесь опреде­ляется двумя числами: абсциссой и ординатой. Абсцисса точки М — это координата точки М\ на оси Ох, а ордината точки М — это координата точки ЛЬ на оси Оу.

Если число х — абсцисса точки М, а число у — ее ордината, то пишут М(х,у) — и говорят, что точка М имеет координаты X и у.

Таким образом, прямоугольная система координат позволяет каждой точке плоскости поставить в соответствие единственную пару действительных чисел — координаты этой точки. Справедливо и обратное утверждение: каждая пара действительных чисел (х, у) сопоставляется единственной точке М, имеющей х и у своими координатами.

Подчеркнем еще раз важность координатного метода: с введе­нием координат (т. е. чисел, определяющих положение точки) на прямой и на плоскости появилась возможность решать многие геометрические задачи средствами алгебры, производя вычисления с числами, а это, в свою очередь, дало возможность применять ЭВМ к решению геометрических задач. И наоборот, при помощи координатной прямой и координатной плоскости можно наглядно решать многие алгебраические задачи.

Понятие координат точек на прямой и на плоскости было впервые введено в геометрию французским ученым и философом Рене Декартом в XVII веке. Это событие явилось началом новой эры в математике — эры рождения и развития понятий функции и геометрического преобразования.

По имени Рене Декарта прямоугольные координаты на плоскости называют еще декартовыми.

Но как связано с именем Декарта, жившего в XVII веке, понятие декартова произведения множеств, введенное в математику в конце XIX века? Чтобы ответить на этот вопрос, выясним сначала, как используют прямоугольную систему координат для наглядного пред­ставления декартова произведения двух числовых множеств.

Пусть Л и В — числовые множества. Тогда элементами декар­това произведения этих множеств будут упорядоченные пары чисел. Изобразив каждую пару чисел точкой на координатной плоскости, получим фигуру, которая и будет наглядно представлять декартово произведение множеств Л и В.

Изобразим на координатной плоскости декартово произ'ведение множеств Л и В, если:

В = {3, 5} в = [3, 51 в = [3, 51 В = [3, 5]

в=в.

1. Л ={1, 2. 3).

Л = (1, 2. 3),

АФ[\. 3],

Л = Я,

А = К.

В случае 1 данные множества конечны и содержат небольшое число элементов, поэтому можно перечислить все элементы их декартова произведения: Л X В = {(1, 3), (1, 5), (2, 3), (2, 5), (3, 3), (3, 5)(.

Построим оси координат и на оси Ох отметим элементы мно­жества Л, а на оси Оу — элементы множества В. Затем изобразим каждую пару чисел из множества ЛхВ точкой на координатной плоскости (рис. 50). Получен­ная фигура из шести точек и будет наглядно представлять декартово произведение множеств Л и В.

В случае 2 перечислить все элементы декар­това произведения множеств невозможно, по­скольку множество В бесконечное.

1 2 3 *

Рис. 50

м /. а

III

Р Я 5

1 2 3 X

Но можно представить процесс образования этого декартова произведения: в каждой паре первая компонента либо 1, либо 2, либо 3, а вторая компонента — действительное число из промежутка [3, 5]. Все пары, первая компонен­та которых есть число I, а вторая про­бегает значения от 3 до 5 включительно, изобра­жаются точками отрезка РМ\ пары, первая ком­понента которых равна 2, а вторая принимает все действительные значения из промежутка [3, 5],— точками отрезка КВ, а пары, первая компонента которых есть число 3, а вторая — любое дейст­вительное число из промежутка [3, 5],— точка­ми отрезка 5(? (рис. 51).

Рис. 51

Таким образом, в случае 2 декартово произ-

ведение множеств Л и В на координатной плоскости изобра­жается в виде отрезков РМ, /СВ, 5(?.

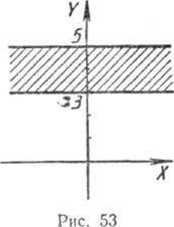
Случай 3 отличается от рассмотренного случая 2 тем, что здесь бесконечно не только множество В, но и множество А. Это при­водит к тому, что первой компонентой пары, принадлежащей мно- жесту ЛХВ, могут быть не только концы промежутка [1, 3], но и любое число этого промежутка. Поэтому точки, изображающие элементы декартова произведения множеств А и В, образуют квад­рат КРМР (рис. 52). Чтобы подчеркнуть, что элементы декартова произведения изображаются точками квадрата, этот квадрат можно заштриховать.

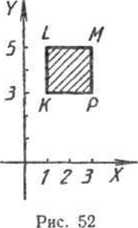
Случай 4 отличается от предыдущего тем, что множество Л состоит из всех действительных чисел, т. е. абсцисса точек, изобра­жающих элементы множества АХВ, пробегает все действительные значения, в то время как ордината выбирается из промежутка [3, 5). Множество таких точек образует полосу (рис. 53).

Декартово произведение КХК (случай 5) состоит из всевозмож­ных пар действительных чисел. Точки, изображающие эти пары, сплошь заполняют координатную плоскость. Таким образом, де­картово произведение РХР содержит столько же элементов, сколько множество точек координатной плоскости.

Рассмотренные примеры показывают, что название «декартово произведение множеств» не случайно: в нем отражена тесная связь между множеством упорядоченных пар чисел и его представлением в декартовой прямоугольной системе координат.

Упражнения

1. Какую фигуру образуют на координатной плоскости точки, изображающие пары чисел (—1, 0), (—1, 4), (3, 0), (3, 4)?

2. Отметьте штриховкой множество точек координатной плос­кости, абсциссы которых отрицательны, а ординаты положительны.

3. Какую фигуру образуют точки, если их абсциссы принадле­жат множеству [ — 2, 2], а ординаты— множеству [ — 3, 3]?

4. Изобразите декартово произведение АХВ в прямоугольной

• • • •

Рис. 54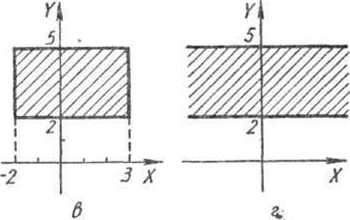

системе координат, если А = (0, 2, 4, 6), а В = {1, 3, 5). Принадлежит ли построенной фигуре точка (2, 3)? А точка (3, 0)?

5. Определите, декартово произведение каких множеств X и У изображено на рисунке 54.

6. Изобразите в прямоугольной системе координат множество ЛХВ, если:

1. Л =[—2, 2], В = {2, 3, 4};

2. Л =[-2, 2], В = [2, 41;

3. Л =/?, в=[2, 4].

7. Покажите графически, что декартово умножение множеств

Л = {3, 2, 1} и В — { 4, 4, 6} не обладает переместительным

свойством.

20. Некоторые задачи, связанные с декартовым умножением

конечных множеств

Мы познакомились с новой операцией над множествами — де­картовым умножением. Получая различные декартовы произведения,

мы особенно внимательно следили за тем, чтобы получить все его элементы, не пропустить ни одного. Но как проверить, все ли эле­менты декартова произведения заданных множеств перечислены? Другими словами, как, зная число элементов в множестве Лив множестве В, определить число элементов в декартовом произ­ведении ЛХВ? Ответ на этот вопрос дает следующая теорема:

Теорема. Если множество А содержит т элементов, а мно­жество В — п элементов, то декартово произведение ЛХВ со­держит ТП'П элементов.

Доказательство. Пусть Л = {<21, а₂, ..., аД В — (Ь 1, Ь₂,..., Ь„]. Тогда множество ЛХВ состоит из всевозможных пар:

(а,, д,), (а,, Ь₂), .... (а,, Ь„),

(а₂, Ь1), (а₂, Ь₂), ..., (а₂, Ь„),

(а_т, 61), (а_т, Ь₂), ..., (а„, Ь_п).

В каждом столбце этой таблицы т пар, а таких столбцов п. Значит, всего в множестве ЛХВ содержится т-п элементов.

Доказанную теорему можно распространить и на декартово произведение п множеств, т. е.

п{А\ХА₂Х-ХА_п) = п(А_[)-п {Ап (А_п).

Задача. Сколько элементов в декартовом произведении АХА, если Л={а, Ь, с, с], е\>

Решение. Так как в множестве А содержится 5 элементов, то в декартовом произведении АХА будет 5-5 = 25 пар.

Правило подсчета числа пар декартова произведения двух конечных множеств и его обобщение на случай п множеств широко используются при решении так называемых комбинаторных задач.

Комбинаторные задачи — это задачи, связанные с составлением из элементов конечных множеств по некоторым правилам различ­ных комбинаций.

Так, в задаче «Используя цифры 4, 2, 8, напишите все воз­можные двузначные числа так, чтобы одна и та же цифра в записи числа не повторялась» требуется рассмотреть различные комбина­ции из цифр 4, 2, 8 при условии, что цифры в этих комбинациях не повторяются. Следовательно, эта задача, а ее решают в начальных классах, комбинаторная.

Раздел математики, занимающийся решением комбинаторных задач, называется комбинаторикой. Комбинаторика играет важную роль в решении ряда проблем теории вероятности, кибернетики, вычислительной техники и в других областях математики.

Заметим, что празило подсчета числа элементов декартова произведения в комбинаторике носит название правила произведения и часто формулируется в таком виде: если элемент х можно выбрать т способами, а элемент у — п способами, то пару (*, у) можно выбрать т-п способами.

Задача 1. Из города А в город В ведут три дороги, а из В в С — две дороги. Сколькими способами можно проехать из А в С через В?

Решение. Представим, что из Л в В ведут дороги 1, 2 и 3, а из В в С — дороги а и б (рис. 55). Тогда из Л в С через В можно проехать следующими способами: (I, а), (1,6), (2, а), (2,6), (3, а), (3, б).

Но можно было решить данную задачу и не прибегая к помощи рисунка, да и все способы проезда из Л в С через В рассматри­вать нет необходимости. Чтобы ответить на вопрос задачи, доста­точно понять, что в ней речь идет о числе д ■/ р, а г^{всевозможных} упорядоченных пар, первая

/ ~2 ч/"—^\ компонента которых выбирается из дорог, ве-

Г" 3 ! * дущих от Л к В, а вторая — из дорог, веду-

щих от В к С. Так как способов выбора

Рис. 55 дорог от Л к В 3, а способов выбора дорог

от В к С — 2, то согласно правилу произведения упорядоченную пару дорог можно выбрать 3-2 = 6 способами.

Задача 2. Сколько трехзначных чисел можно составить, ис­пользуя цифры 5, 6 и 7, если цифры в записи числа: 1) могут повторяться; 2) не повторяются?

Решение. I) Если повторения цифр разрешены, то на каждое место в записи трехзначного числа можно поставить любую из данных трех цифр, т. е. способов выбора первой цифры 3, способов выбора второй цифры тоже 3, способов выбора третьей цифры 3. Следовательно, в этом случае можно составить 3-3-3 = 27 трехзнач­ных чисел. 2) Если цифры в записи числа не повторяются, то способов выбора первой цифры 3, способов выбора второй цифры 2, а способов выбора третьей — 1. Следовательно, в том случае можно составить 3-2-1=6 трехзначных чисел.

Упражнения

1. В множестве А 7 элементов. Сколько элементов в множест­ве В, если в декартовом произведении АхВ содержится: 1) 42 эле­мента; 2) 7 элементов; 3) 0 элементов?

2. Набор составляется из книги и блокнота. Сколько различ­ных наборов можно составить, если имеется 20 видов различных книг и 15 видов различных блокнотов?

3. Сколько двузначных чисел можно составить, используя циф­ры 1, 2, 3, 4, если цифры в записи числа: 1) повторяются; 2) не повторяются?

4. Сколько различных четырехзначных чисел можно составить из цифр I, 2, 4, 6, 8, если каждая из них может быть использована в записи числа только один раз? Сколько среди них таких, которые начинаются с цифры 2?

5. Сколько трехзначных чисел можно составить, используя циф­ры 3, 4, 0, если цифры в записи числа не повторяются?

6. Команда космического корабля состоит из трех человек: ко­мандира, бортинженера и врача. На место командира есть 2 кан­дидата, на место бортинженера — 3, на место врача — 4. Сколь­кими способами может быть составлена команда корабля?

7. Сколькими способами можно рассадить 5 учащихся, если в классе 40 мест?

8. На окружности отмечены 4 точки. Сколько различных хорд они определяют?

9. В классе изучается 10 предметов. В понедельник 5 уроков, причем все уроки разные. Сколькими способами можно составить расписание на понедельник?

10. Для ведения собрания из 36 человек надо выбрать пред­седателя и секретаря. Сколькими способами это можно сделать?

11. 97

    Сколько можно составить четырехзначных чисел, деля­щихся на 5?

4 Заказ 147