§ 3. Математические доказательства 35

13. Дедуктивные рассуждения 35

14. Простейшие схемы дедуктивных рассуждений 41

15. Неполная индукция ’³ 44

16. Способы доказательства истинности высказываний 47

§ 4. Текстовые задачи и их решение 51

17. Понятие текстовой задачи 51

18. Способы решения текстовых задач 53

111111111111111111111III1111 ^>мъ° 56

(л п пс=л п(в п с). (Л1)В)ис=Л11(вис). 79

2) С=((а, (Ь, <Г), (а, с)); 96

□ □ □ о о о о 137

"^{еотрииатель}' ОООООКН8В2 145

«О О О О 141

^□□□□□□000 «О О О О О О 139

□ □□□□□□□□□□□ 158

& . 226

I „ 295

8. Из каких элементов состоит объединение множества букв в

слове «математика» и множества букв в слове «геометрия»?

9. М — множество однозначных натуральных чисел, Р — множе­ство нечетных натуральных чисел. Какие числа войдут в объеди­нение множеств М и Р? Окажутся ли в нем числа 4, 14, 17? Ответ запишите, используя знаки 6 и

10. Найдите объединение множеств решений неравенств, в которых переменная х принимает действительные значения:

1)х> — 2, х>0; 2) х> — 3,7, *<4;

3. х^5, х<—7,5; 4) —2<х-<4, х^— 1;

5. -7<*<5, -6<х<2.

11. Какую фигуру будет представлять объединение-двух тре­угольников, если их пересечением является: 1) треугольник; 2) ше­стиугольник; 3) отрезок?

12. Начертите две фигуры, принадлежащие объединению мно­жеств С и О, если:

1. С — множество квадратов, В — множество прямоугольников;

2. С — множество прямоугольных треугольников, В — множе­ство тупоугольных треугольников.

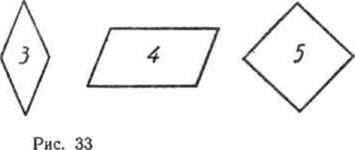
13. Установите, какие из фигур, приведенных на рисунке 33, со­держатся в объединении множества ромбов и множества прямо­угольников.

14. Что представляет собой пересечение треугольника АВС и его стороны АВ? А их объединение?

15. Изобразите на координатной прямой множество тех зна­чений переменной х, при которых обращается в истинное высказы­вание предложение: 1) х^ —-4 и х^1; 2) хг^—2 или х^>2;

3. |*| <3; 4) |*| >4.

16. Назовите все множества, о которых идет речь в задаче:

1. У школы посадили 4 липы и 3 березы. Сколько всего де­ревьев посадили у школы?

2. Пионеры помогали колхозу в уборке моркови. Один отряд собрал 40 корзин моркови, а другой — на 10 корзин больше. Сколько корзин моркови собрали оба отряда?

17. Установите, какое множество является объединением двух других рассматриваемых в задаче: 1) У Коли было б книг. В день рождения ему подарили еще 4 книги. Сколько книг стало у Коли?

2. У дома росли 2 сосны, а у моста — на 4 сосны больше. Сколько сосен росло у моста?

3. На каждой тарелке 5 яблок. Сколько яблок на 3 тарелках?

20. Законы пересечения и объединения множеств

Как известно, операции сложения и умножения чисел подчи­няются ряду законов: переместительному, сочетательному и др.

Существуют ли какие-либо законы для хпераций пересечения и объединения множеств? Существуют, и некоторые из них мы уже использовали. В частности, находя пересечение или объединение множеств, мы не задумывались над порядком оперирования множествами. И это потому, что из определений пересечения и объ­единения множеств вытекает для любых множеств Л и В справед­ливость равенств А (\В = В[)А и А\}В — В[)А, которые представляют собой запись переместительных законов пересечения и объединения множеств.

Для пересечения и объединения множеств справедливы также сочетательные законы: для любых множеств Л, В и С выполняют­ся равенства

(л п пс=л п(в п с). (Л1)В)ис=Л11(вис).

Заметим, что назначение скобок в этих записях то же, что и в записях операций над числами.

Наглядно представить сочетательные законы можно при помощи кругов Эйлера. Рассмотрим, например, сочетательный закон пере­сечения множеств. Изобразим множества Л, В и С в виде трех попарно пересекающихся кругов (рис. 34). В выражении (ЛПВ)ПС скобки определяют порядок действий: сначала выполняется пере­сечение множеств Л и В — оно отмечено на рисунке 34, а верти­кальной штриховкой, а затем находят пересечение полученного мно­жества и множества С. Если отметить множество С горизонтальной штриховкой, то область, заштрихованная дважды, и будет изобра­жать множество (ЛПВ)ПС.

Обратимся теперь к рисунку 34, б. Здесь сначала выполняется пересечение множеств В и С — оно отмечено на рисунке верти­кальной штриховкой, а затем находят пересечение множества Л с полученным множеством. Если отметить множество Л горизонталь­ной штриховкой, то область, заштрихованная дважды, и будет изображать множество ЛП(ВГ)С).

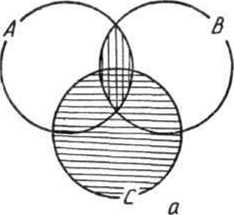
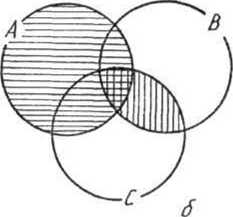
Видим, что области, представляющие на рисунке множества (Л Л В) Л С и ЛП(вПС). одинаковы, что и подтверждает справед­ливость сочетательного закона пересечения множеств.

Аналогично можно выполнить иллюстрацию и для сочетательного закона объединения множеств.

Каково назначение рассмотренных сочетательных законов? Они объясняют, как находить пересечение и объединение трех множеств, зная правило для двух. Кроме того, на основании сочетательных законов скобки в выражениях (Л Л В) Л С, Л Л (В ПС) можно опускать и писать: ЛЛВЛС ЛЛВЛС.

Сочетательные законы пересечения и объединения йножеств можно распространить на любое число множеств.

Пересечение и объединение множеств связаны друг с другом распределительными законами: для любых множеств Л, В и С справедливы равенства

(Л1|В)ЛС = (ЛЛС)1)(ЛЛС), (1)

(ЛПВ)1|С = (Л11С)П(В1|С). (2)

Заметим, что если в выражении есть знаки пересечения и объеди­нения и нет скобок, то сначала выполняют пересечение, так как

считают, что операция пересечения более «сильная», чем объеди­

нения. В связи со сказанным запись распределительного закона пере­сечения относительно объединения (1) можно упростить, опустив скобки в правой части равенства.

Упражнения

1. Принадлежит ли элемент х объединению множеств Л, Б и С, если:

1) хбЛ; 2) х^А и х^В\ 3) х^А, х^В и х^С\ 4) х^А, но х{С;

5. х$А, но и х^В?

2. Сформулируйте условия, при которых элемент у будет при­надлежать множеству ЛПВЛС.

3. В каком порядке надо выполнять действия над множества­ми в выражении:

1. Л Л ВО С; 2) ЛП(ВУС); 3) А{\В[\С?

4. Л — множество натуральных чисел, меньших 20, а В, С и О — его подмножества, причем В состоит из чисел, кратных 3, С — из чисел, кратных 4, О — из четных чисел. Какие числа являются элементами множеств:

1. (Л Л В) ПС; 3) АЩВЦС)-, 5)ЛЛВуС;

2. ЛП(ВЛС); 4) (Л Л В)у С; 6) Л Л (В Л С)?

Назовите среди множеств пары равных.

5. Используя круги Эйлера, проиллюстрируйте справедливость:

1. сочетательного закона объединения множеств;

2. распределительного закона пересечения относительно объе­динения.

Рис. 35

6. Рис. 36

   Установите, какая из областей, выделенных штриховкой на рисунках 35 и 36, изображает множество ЛуВЛС.

7. X — множество двузначных чисел, У — множество четных чи­сел, Р — множество чисел, кратных 4. Каковы характеристические свойства элементов множеств А=Хр[У [\Р и В = (А Ч К) П Я?

Изобразите множества X, У, Р, А и В при помощи кругов Эйлера. Назовите три числа, принадлежащие множеству Л, и три числа, принадлежащие множеству В.

8. Л — множество ромбов, В — множество треугольников, С — множество многоугольников, содержащих угол 60°. Начертите две фигуры, принадлежащие множеству А = ЛПСиВПС.