§ 3. Математические доказательства 35

13. Дедуктивные рассуждения 35

14. Простейшие схемы дедуктивных рассуждений 41

15. Неполная индукция ’³ 44

16. Способы доказательства истинности высказываний 47

§ 4. Текстовые задачи и их решение 51

17. Понятие текстовой задачи 51

18. Способы решения текстовых задач 53

111111111111111111111III1111 ^>мъ° 56

(л п пс=л п(в п с). (Л1)В)ис=Л11(вис). 79

2) С=((а, (Ь, <Г), (а, с)); 96

□ □ □ о о о о 137

"^{еотрииатель}' ОООООКН8В2 145

«О О О О 141

^□□□□□□000 «О О О О О О 139

□ □□□□□□□□□□□ 158

& . 226

I „ 295

множество прямоугольных треугольников; 4) А — множество квад­

ратов, В — множество прямоугольников с равными сторонами.

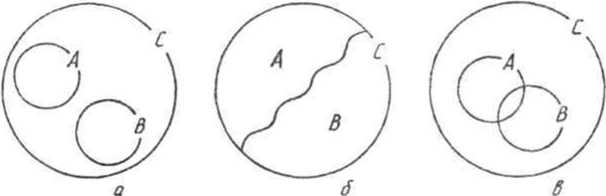
7. Изобразите при помощи кругов Эйлера отношения между множествами Л, В и С, если известно, что: 1)Лсй и ВсС\

2. Ас.В, С пересекается с В, но не пересекается с Л; 3) Л, В и С пересекаются, но ни одно не является подмножеством другого.

8. Приведите примеры множеств X, У и 2, чтобы отношения между ними были такими, как на рисунке 25.

9. Дано множество А=[а, Ь, с, (I). Образуйте все подмно­жества А, содержащие: 1) два элемента; 2) три элемента.

10. Образуйте всевозможные подмножества множества Р = (3,

5. 7. 9).

11. Установите, с какими теоретико-множественными понятия­ми встречаются учащиеся начальных классов, выполняя задание:

1. запиши по порядку числа от 10 до 19. Подчеркни и прочитай четные числа; 2) из ряда чисел от 1 до 20 выпиши по порядку чис­ла, которые делятся без остатка на 5; 3) из чисел 27, 45, 38, 62, 53, 72, 8, 48 выпиши те, которые при делении на 5 дают в остатке 3.

20. Множества и понятия

Как известно, любое понятие имеет объем. Ранее мы говорили об объеме понятия, названного некоторым термином, как о сово­купности объектов, которые можно назвать этим термином. С тео­ретико-множественных позиций объем понятия — это множество объектов, которые можно назвать словом, обозначающим поня­тие. Например, объем понятия «треугольник» — множество треуголь­ников, объем понятия «прямой угол» — множество прямых углов.

Подход к объему понятия как множеству дает возможность наглядно представлять отношения между понятиями.

Рассмотрим два понятия: понятие а — «прямоугольник» и по­нятие Ь — «квадрат». Обозначим их объемы соответственно бук­вами А и В. Так как всякий квадрат является прямоугольником, то при помощи кругов Эйлера отношения между объемами дан­ных понятий изображаются так, как на рисунке 26. В этом слу­чае говорят, что понятие «прямоугольник» является родовым по отношению к понятию «квадрат», а понятие «квадрат» — видовым по отношению к понятию «прямоугольник».

Существуют понятия, которые не находятся в отношении рода и вида. Например, понятия «квадрат» и «треугольник» — их объе­мы не находятся в отношении включения.

Понятия рода и вида относительны: одно и то же понятие мо­жет быть родовым по отношению к одному и видовым по отно­шению к другому. Например, понятие «прямоугольник» родовое по отношению к понятию «квадрат» и видо­вое по отношению к понятию «четырех­угольник».

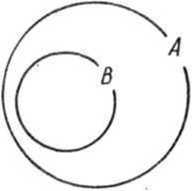
Для одного и того же понятия можно ука­зать несколько родовых по отношению к нему понятий. Так, для понятия «прямоугольник» родовыми являются понятия «четырехуголь­ник», «параллелограмм», «многоугольник».

Среди них можно указать ближайшее. Для понятия «прямоугольник» ближайшим родо­вым понятием является понятие «параллело­грамм». ■ Рис. 26

1. Изобразите при помощи кругов Эйлера отношения между объемами понятий а и Ь, если:

1. а — «треугольник», Ь — «прямоуголушй треугольник»;

2. а — «прямая», Ь — «отрезок»;

3. а — «равнобедренный треугольник», Ь —- «тупоугольный тре­угольник».

2. Покажите при помощи кругов Эйлера, что понятие «пря­моугольник» видовое по отношению к понятию «четырехугольник», и назовите свойства четырехугольников, которыми обладают пря­моугольники.

3. Изобразите при помощи кругов Эйлера высказывания:

1. Все числа, кратные 6, кратны и 3.

2. Среди чисел, кратных 7, есть числа, кратные 5.

3. Среди нечетных чисел нет ни одного числа, которое делилось бы на 4.

4. Даны понятия: а — «четное натуральное число», Ь — «нечет­ное натуральное число», с — «натуральное число». В каком слу­чае на рисунке 27 изображены отношения между объемами данных понятий (объемы обозначены соответственно А, В, С)?

5. Изобразите при помощи кругов Эйлера отношения между понятиями а, Ь и с, если:

1. а — «однозначное число», Ь — «двузначное число», с — «на­туральное число»;

2. а — «треугольник», Ь — «равносторонний треугольник», с — «равнобедренный треугольник»;

3. а — «прямые, лежащие в одной плоскости», Ь — «параллель­ные прямые», с — «пересекающиеся прямые»;

4. а — «натуральное число», Ь — «целое число», с — «рацио­нальное число».

6. Приведите примеры понятий, отношения между которыми изо­бражаются так, как на рисунке: 1) 27, а; 2) 27, в.