§ 5. Множества и операции над ними
Понятия множества и элемента множества
В математике часто приходится рассматривать те или иные группы объектов как единое целое: ч^исла от 1 до 10, натуральные числа, однозначные числа, треугольники, квадраты и т. д. Все эти различные совокупности называют множествами.
Понятие множества является одним из основных понятий математики и поэтому не определяется через другие. Его можно пояснить на примерах. Так, можно говорить о множестве учащихся некоторого класса, о множестве гласных букв русского алфавита, о множестве натуральных чисел.
Математический смысл слова «множество» отличается от того, как оно используется в обыденной речи, где его связывают с большим числом предметов. В математике этого не требуется. Здесь рассматривают множество, состоящее из одного объекта, и множество, не содержащее ни одного объекта.
В некоторых случаях множества обозначают буквами латинского алфавита: А, В, С, ..., 2. Множество, не содержащее ни одного объекта, называют пустым и обозначают знаком 0.
Объекты, из которых образовано множество, называют его элементами. Элементы множества принято обозначать строчными буквами латинского алфавита: а, Ь, с г.
В математике и других науках нередко приходится выяснять, принадлежит какой-либо объект рассматриваемому множеству или не принадлежит. Например, мы говорим, что число 5 натуральное. Другими словами, мы утверждаем, что число 5 принадлежит множеству натуральных чисел. Или, например, говорим, что число 0,75 не является натуральным. Это означает, что число 0,75 не принадлежит множеству натуральных чисел.
Предложение вида «Объект а принадлежит множеству А» можно записать, используя символы: оеЛ. Прочитать его можно по-разному:
Объект а принадлежит множеству А.
Объект а — элемент множества А.
Множество А содержит элемент а.
Предложение «Объект а не принадлежит множеству А» можно записать так: а&А. Его читают:
Объект а не принадлежит множеству А.
Объект а не является элементом множества А.
Множество А не содержит элемента а.
Пусть А — множество однозначных чисел. Тогда предложение «ЗеЛ» можно прочитать: «Число 3 однозначное», а запись «12^ёА» означает; «Число 12 не является однозначным».
Множества бывают конечные и бесконечные. Так, множество дней педели конечно, а множество точек на прямой бесконечно. Бесконечными являются и такие множества, как множество натуральных чисел, множество целых чисел, множество рациональных чисел, множество действительных чисел. Для этих множеств в математике приняты специальные обозначения: буковой N обозначают множество натуральных чисел, 2 — множество целых чисел, р — множество рациональных чисел, К — множество действительных чисел.
Упражнения
Назовите три элемента множества: 1) предметов, изучаемых в педагогическом училище; 2) звонких согласных букв русского алфавита; 3) натуральных чисел.
Прочитайте различными способами предложения: I) 12еХ*,
-З&Х.
В — множество четных чисел.
Прочитайте следующие высказывания и укажите среди них истинные:
100е=ЛГ; 2) -8б2; 3)
5,36 е=<?, 5) 102^ К; 6) л/2(=<1\
7) -7е«; 8) |-€=ЛГ; 9) 0е=2.
Р — множество натуральных чисел, больших 7 и меньших 14. Выясните, принадлежат или не принадлежат этому множеству числа 13, 10,
5, 7, 14. (Ответ запишите, используя знаки е и
О — множество целых отрицательных чисел. Назовите пять чисел, принадлежащих этому множеству. Верно ли, что — 1еД; 0^0; — 3,2еД?
Даны числа: 325; 0; —17; —3,8;
Установите, какие из них принадлежат множеству: 1) натуральных чисел;
целых чисел; 3) рациональных чисел; 4) действительных чисел.
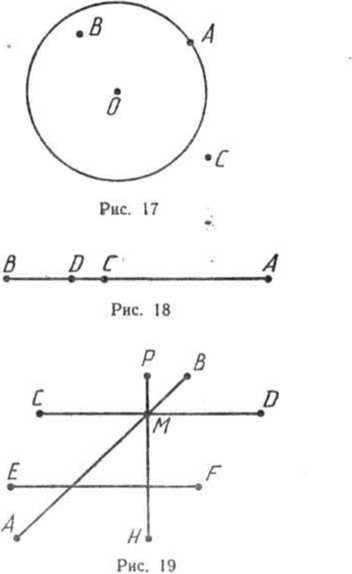
М — множество точек окружности, изображенной на рисунке 17. Прочитайте следующие предложения и укажите среди них верные: 1) Л<=Л1; 2) ОеМ; 3) ВбМ; 4) С§ёМ.
Измените условие задачи 8 так, чтобы все высказывания были верными.
Запишите множество отрезков, которым принадлежит
точка С (рис. 18).
Запишите с помощью знаков е и какие из отрезков
АВ, СО, ЕР и РН проходят через точку М, а какие через нее не
проходят (рис. 19).