7.5. Задача о трех станках

Правило для трёх станков.

1. Обрабатывать раньше те детали, у которых время обработки на первом станке минимально.

2. Обрабатывать раньше те детали, у которых время обработки на последнем станке максимально.

3. Обрабатывать раньше те детали, у которых узкое место (т. е. станок с наибольшим временем обработки данной детали) находится дальше от начала процесса обработки.

Порядок запуска: 3; 1; 4; 5; 2.

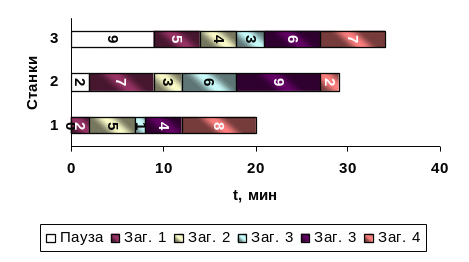
Рис. 15

7.6. Выводы

Вручную удалось подобрать оптимальное решение, отличающиеся от решения задачи на ЭВМ на 5 мин.

8. Лабораторная работа №8

ИССЛЕДОВАНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ОДНОКАНАЛЬНОЙ СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ С ОЖИДАНИЕМ

(станок и буферный склад)

8.1. Цель работы

1. Освоить методы анализа аналитической модели одноканальной системы массового обслуживания с ожиданием.

2. Освоить методы расчета параметров модели СМО.

8.2. Дифференциальные уравнения, характеризующие СМО

, (8.1)

где – вероятность нахождения системы в момент времени в состоянии s_i.

8.3. Уравнение математической модели

, (8.2)

где Р₀ – вероятность работоспособности системы в установившемся режиме.

8.4. Графики для базового варианта

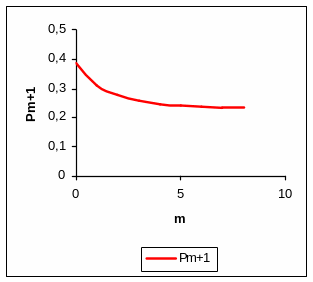
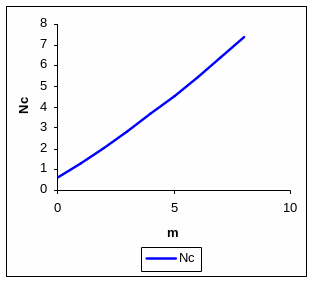
Рис. 16 Рис. 17

8.6. Расчеты операционных характеристик

, (8.3)

,

(8.4)

,

(8.5)

А = 0,029 (1 – 0,2330) = 0,022.

, (8.6)

мин.

(8.7)

мин.

, (8.8)

мин.

8.7. Результаты графического исследования

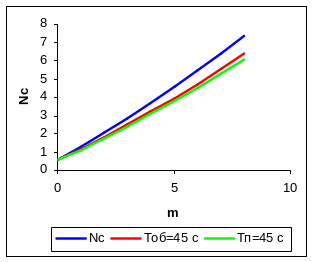
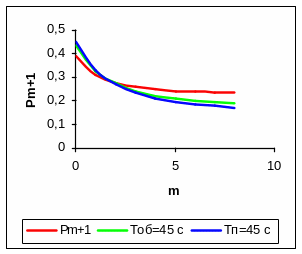
Рис. 18 Рис. 19

8.8. Выводы

Графическое исследование модели показало, что снижение времени обработки стопы до 45 мин. и увеличение промежутка между поступлением строк на обработку до 45 мин. ведет к снижению среднего числа заявок, находящихся в системе. При этом, вероятность отказа системы снижается при m > 2, а m < 2 возрастает.