5. Лабораторная работа №5

ИССЛЕДОВАНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ

ЛИНЕЙНОЙ РАСПРЕДЕЛИТЕЛЬНОЙ ЗАДАЧИ

(оптимальное распределение ресурсов предприятия)

5.1. Цель работы

1. Освоить способы формализованного представления задачи формирования оптимальной производственной программы.

2. Изучить возможности метода решения задачи.

5.2. Словесная формулировка задачи

Требуется определить такое количество каждого из двух видов выпускаемой продукции, которое позволит: не превысить все виды ресурсов; удовлетворить спрос на продукцию; получить максимальную прибыль предприятия.

5.3. Формулировка задачи в общем виде и

математическая модель оптимизационной задачи

Требуется отыскать неотрицательные значения переменных x_j, удовлетворяющих линейным ограничениям следующего вида

; (5.1)

; (5.2)

; (5.3)

(5.4); (5.5)

обеспечивающих достижение максимума следующей линейной функции, характеризующей прибыль предприятия.

5.4. Результаты решения задачи

В результате решения задачи на ЭВМ получено следующее оптимальное решение (см. распечатку)

шт.; шт.

Максимальная прибыль составляет 67519 руб.

5.5. Проверка ограничений

Выполнение условия спроса = 200; < 250.

Ограничения по ресурсам

;

;

.

Максимальная прибыль

руб.

5.6. Анализ задачи на чувствительность

Для анализа построим область допустимых решений, удовлетворяющих ограничениям (5.1) – (5.5) .

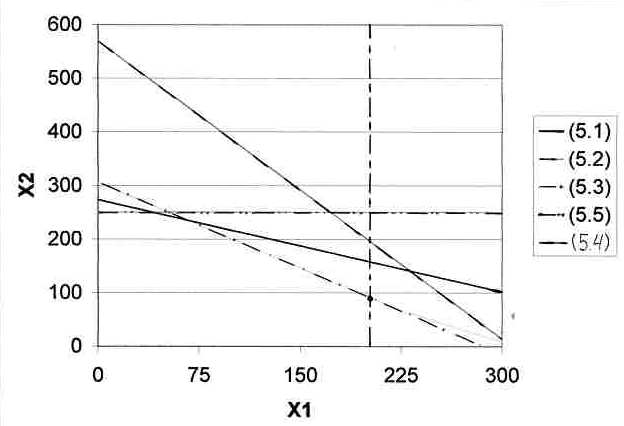Рис. 10

Активными ресурсами являются запасы смолы (линия (5.3)), а пассивными все остальные.

Рассчитаем предельные значения пассивных ограничений, не изменяющих оптимальные ограничения. Подставив в левую часть (5.1) координаты оптимальной точки, получим минимальный запас соснового сырья, не изменяющего оптимальное решение.

м³.

Минимальный спрос также определится координатами оптимальной точки.

Для ФСФ = 200 м³; для ФБВ = 92 м³, что соответствует решению на ЭВМ (см. распечатку). Область допустимых решений новой модели представлена на рис. 11.

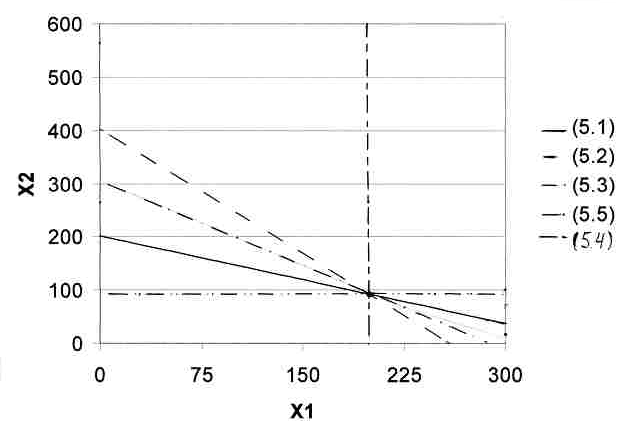
Рис. 11

Определим ценность единицы ресурса (5.3). Следует отметить, что пассивные ресурсы имеют нулевую ценность. Прямую (5.3) можно «сдвигать» параллельно самой себе до достижения точки B, координаты этой точки определятся решением системы из уравнений (5.1) и (5.4).

, (5.6)

решение системы м³; м³. Запас ресурса (5.3) при этом составит

кг.

Максимальная прибыль при этом составит

руб.

Ценность единицы ресурса (5.3) составит

руб./кг.