3. Лабораторная работа №3
Исследование математической
Модели процесса прогрева
(Прессование древесностружечных плит)
3.1. Цель работы
1. Освоить численные методы решения уравнений детерминированной модели процесса прогрева при прессовании ДСтП.
2. Освоить способы расчета и отображения переходного процесса прогрева.
3.2. Дифференциальное уравнение, характеризующее процесс
Процесс прогрева рассматривается по толщине пакета, при этом можно воспользоваться одномерной моделью
,
(3.1)
где t – температура, 0С;
– текущее время процесса прогрева, с;
a – коэффициент температуропроводности материала;
x – координата точки.
3.3. Формула расчета частных производных
по конечно-разностной схеме
Первая производная рассчитывается по формуле
,
(3.2)
где n – номер точки на координате времени;
– шаг дискретизации времени, с.
Вторая производная рассчитывается по формуле
,
(3.3)
где j – номер точки на координате x;
– шаг
точек по толщине пакета.
3.4. Уравнение, позволяющее рассчитать температуру
в пространственно-временной области
Уравнение имеет вид
.
(3.4)
3.5. Результаты расчетов распределения
температуры для указанной точки
0С,
0С,
0С,
0С.
3.6. Профили распределения температур по толщине брикета
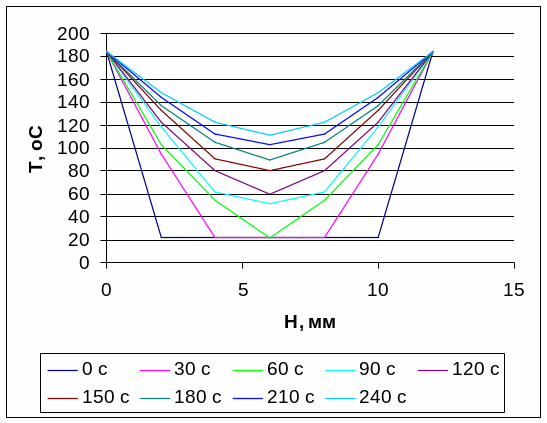
Рис. 9
3.7. Результаты определения времени прогрева
брикета до заданной температуры
Принимаем время прогрева = 240 c (см. распечатку и рис. 9).
3.8. Выводы
Заданная температура в центре брикета Т = 100 0С достигается за 240 с. При этом, ближайшие к плитам пресса точки по толщине прогреваются до 141,05 0С. Перепад температуры по толщине брикета составляет 141,05 –102,10 = 38,95 0С.
4. Лабораторная работа №4
ИССЛЕДОВАНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
ЛИНЕЙНОЙ РАСПРЕДЕЛИТЕЛЬНОЙ ЗАДАЧИ
(формирование оптимальной производственной программы)
4.1. Цель работы
1. Освоить способы формализованного представления задачи формирования оптимальной производственной программы.
2. Изучить возможности метода решения задачи.
4.2. Словесная формулировка задачи
Требуется так распределить изделия по видам оборудования, чтобы получить максимальную прибыль предприятия с учетом имеющихся ресурсов оборудования.
4.3. Формулировка задачи в общем виде и
математическая модель оптимизационной задачи
Требуется отыскать неотрицательные значения переменных xj, удовлетворяющих линейным ограничениям следующего вида
;
;
;
обеспечивающих достижение максимума следующей линейной функции, характеризующей прибыль предприятия.
4.4. Результаты решения задачи
В результате решения задачи на ЭВМ получено следующее оптимальное решение (см. распечатку)
шт.;
шт.;
шт.
Максимальная прибыль составляет 263889 руб.
4.5. Проверка ограничений
Выполнение плана шт.> 20; шт.= 50; шт.= 60.
Ограничения по ресурсам
;
;
.
Максимальная прибыль
руб.
4.6. Выводы
В результате решения задачи на ЭВМ получено оптимальное решение, обеспечивающее выполнение заданного плана выпуска продукции с учетом количества имеющихся ресурсов, при этом максимальная прибыль составила 264000 руб.