
- •1.4. График переходного процесса смешения лкм для базового варианта задания
- •1.5. Определение постоянной времени переходного процесса
- •1.6. Результаты графического исследования модели процесса
- •1.7. Выводы
- •2.1. Цель работы
- •2.3. Уравнения математической модели процесса
- •2.4. Расчет производных и для 2-х контрольных точек
- •3. Лабораторная работа №3
- •Исследование математической
- •Модели процесса прогрева
- •(Прессование древесностружечных плит)
- •3.1. Цель работы
- •4. Лабораторная работа №4
- •4.1. Цель работы
- •5. Лабораторная работа №5
- •5.1. Цель работы
- •5.4. Результаты решения задачи
- •5.5. Проверка ограничений
- •5.6. Анализ задачи на чувствительность
- •5.7. Выводы
- •6. Лабораторная работа № 6
- •6.1. Цель работы
- •6.4. Частная графовая модель транспортной задачи для оптимального варианта решения
- •6.5. Проверка ограничений
- •135 М3 предложение не удовлетворено
- •285М3 предложение не удовлетворено
- •160 М3 м3 предложение удовлетворено
- •6.6. Выводы
- •7. Лабораторная работа №7 исследование задачи оптимального порядка запуска деталей на обработку
- •7.1. Цель работы
- •7.2. Схема деревообрабатывающего участка мебельного производства
- •7.3. Правило Джонсона для двух станков
- •7.4. Задача о двух станках
- •7.5. Задача о трех станках
- •8. Лабораторная работа №8
- •8.1. Цель работы
- •9. Лабораторная работа №9
- •9.1. Цель работы
Министерство образования Российской Федерации
Санкт-Петербургский Лесотехнический университет
имени С. М. Кирова
Кафедра технологии деревообрабатывающих производств
Отчет по лабораторным работам:
№ 1; 2; 3; 4; 5; 6; 7; 8; 9
Выполнил: студент
П роверил:
преподаватель
роверил:
преподаватель
Санкт-Петербург
1. ЛАБОРАТОРНАЯ РАБОТА №1
ИССЛЕДОВАНИЕ МАТЕМАТИЧЕСКОЙ
МОДЕЛИ ПРОЦЕССА ПРИГОТОВЛЕНИЯ
ЛАКОКРАСОЧНОГО МАТЕРИЛА
1.1. Цель работы
1. Освоить методы анализа аналитической модели процесса смешения ЛКМ.
2. Освоить методы расчета параметров переходного процесса.
1.2. Схема процесса смешения
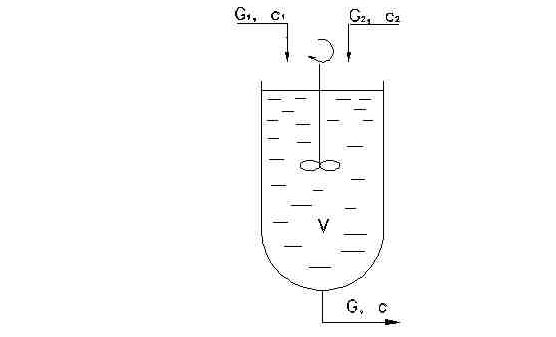
Рис. 1.
1.3. Уравнения процесса
Процесс смешения характеризует следующее дифференциальное уравнение
![]() ,
(1.1)
,
(1.1)
где V – объем смесителя, дм3;
с – концентрация растворителя на выходе, %;
G1 – расход ЛКМ, дм3/с;
с1 – концентрация растворителя в ЛКМ на входе, %;
с2 – концентрация растворителя на входе, %;
G2 – расход растворителя, дм3/с;
t – время протекания процесса, с.
Уравнение математической модели процесса смешения ЛКМ имеет вид
![]() ,
(1.2)
,
(1.2)
где
![]() – концентрация растворителя в ЛКМ во
время
– концентрация растворителя в ЛКМ во
время
![]() ,
%;
,
%;
с0 – начальная концентрация, например остаток от предыдущей смены, %;
– текущее время протекания процесса, мин;
Т – постоянная времени протекания процесса, мин.
1.4. График переходного процесса смешения лкм для базового варианта задания
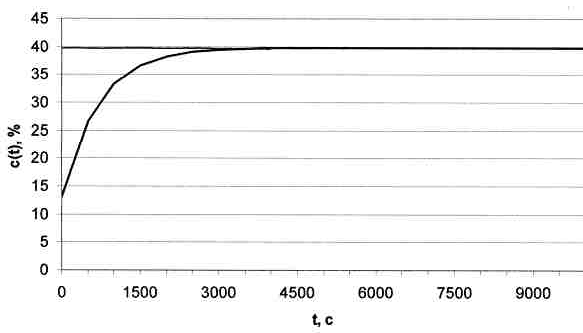
Рис. 2
1.5. Определение постоянной времени переходного процесса
1. Графоаналитический метод
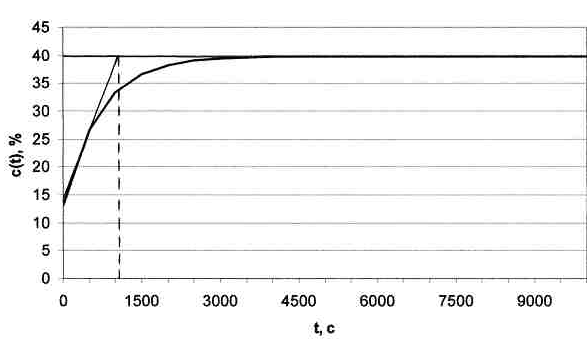
Рис. 3
Постоянная времени Т = 1050 с.
2. Логарифмический метод
Для нахождения постоянной времени логарифмическим методом рассмотрим функцию
![]() ,
(1.3)
,
(1.3)
где
![]() –
концентрация растворителя в ЛКМ при
–
концентрация растворителя в ЛКМ при
![]() ,
%;
,
%;
k
=![]() .
.
Значение определится значением выражения из формулы (1.2)
![]() ,
(1.4)
,
(1.4)
![]()
Подставив в уравнение (1.3) необходимые значения (при этом значение постоянной времени Т для определения k определяется графоаналитическим методом), получим
![]() ,
(1.5)
,
(1.5)
и построим график этой функции.
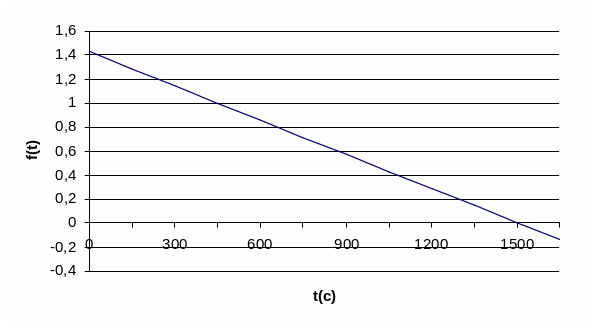
Рис. 4
Определим значение постоянной времени
![]() с.
с.
1.6. Результаты графического исследования модели процесса
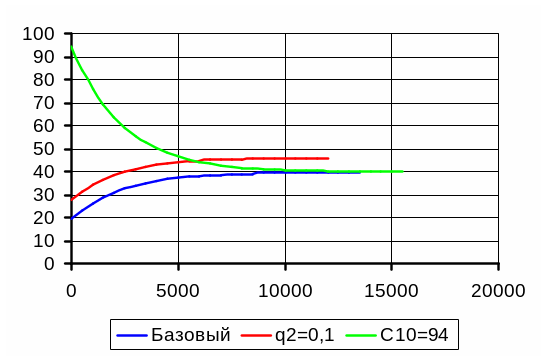
1.7. Выводы
По результатам графического исследования математической модели процесса смешения ЛКМ, можно утверждать, что увеличение расхода растворителя до q2=0.1 дм3/с, влечет за собой увеличение времени протекания процесса. При это постоянная времени Т= V/G увеличивается. Увеличение концентрации растворителя на входе до С10 = 94 % не влияет на постоянную времени Т, а процесс смешения при этом происходит несколько дольше, также при этом уменьшается концентрация растворителя на выходе.
ЛАБОРАТОРНАЯ РАБОТА №2
ИССЛЕДОВАНИЕ МАТЕМАТИЧЕСКОЙ
МОДЕЛИ ПРОЦЕССА ОТВЕРЖДЕНИЯ
(формирование клеевых соединений)
2.1. Цель работы
1. Освоить методы анализа аналитической модели процесса отверждения при формировании клеевых соединений.
2. Освоить методы идентификации математической модели и расчета параметров переходного процесса.
2.2. Дифференциальное уравнение, характеризующее процесс
Система дифференциальных уравнений, характеризующих процесс отверждения, имеет вид
![]() ,
(2.1)
,
(2.1)
где CA; CR; CS – концентрации исходного, промежуточного, конечного продуктов соответственно, %;
k1; k2 – константы, определяющие скорость реакции;
– текущее время протекания процесса, с.
2.3. Уравнения математической модели процесса
Математическая
модель изотермического способа
отверждения продукта при начальных
условиях
![]() ,
,
![]() ,
,
![]() имеет вид:
имеет вид:
на первой стадии
![]() ,
(2.2)
,
(2.2)
на второй стадии
![]() .
(2.3)
.
(2.3)
