2.2 Құбырлы дайындамаға үздіксіз қалыпқа келтірген кезде жолақтың кернеулі-түр өзгерген жағдайын зерттеу және есептеудің әдістемесі

Құбырлы дайындаманың орта бетінің кернеулі-түр өзгерген жағдайын (КТЖ) есептеу әдістемесі бұрғылаудың көп радиусты сызбаларында жолақтың серпімді пластикалық түр өзгеруін ескереді.

Берілген міндетті шешкен кезде келесі жорамалдар қабылданды: — қалыпқа келтірудің ошағының шеткі сол жақ көлденең қимасында, жолақтың түйісетін жиектерінде және қалыпқа келтірудің ошағының шеткі оң жақ қимасында күштер жоқ; қалыпқа келтірудің күштері қалыпқа келтіру ошағының бетіне перпендикулярлы бағытталған; қалыпта өзгертудің есептік үрдісі үін бұрғылаудың геометриялық ошағы өзгермейді. КТЖ есептеу аспап пен дайындаманың байланысты өзара әрекеттесуінің механизмінің әсерін жою үшін дайындаманың орта беті үшін ғана жүзеге асырылды.

Құбырлардың әр түрлі тип өлшемдері үшін берілген әдістемені пайдалану әрекеті көп параметрлі беттің түр өзгеру ошағын геометриялық сипаттаудың қажеттілігіне әкелді, ал жоғары қоспаланған болаттардан құбырларды қалыпқа келтіруді зерттеу кезінде жүргізілген сараптамалық зерттеулер Гук заңының көмегімен кернеулер мен түр өзгерулердің арасында өзара байланысты пайдаланған кезде әдістеменің шектеулілігін көрсетті.

Қалыпқа келтірілетін жолақтың орта жазықтығымен X, Y координаталарының тікбұрышты лагранжды жүйесі байланысты. Сонымен бірге, орта жазықтықтың әрбір материалдық нүктесіне қалыпқа келтіру барысында өзгермейтін сандардың жұбы (X, Y) сәйкестікке қойылды.

Түр өзгеру ошағының орташа беті кейін X,Y, Z координаталарының эйлерлік жүйесінде сипатталады (15 сур). Егер х = const жолағының қимасы туынды нүктесіне у координаталық осімен жазықтыққа жобалаған кезде шеңберді айналу нүктесінен есептелетін L доғасының ұзындығы сәйкес келетін R(x) радиусының шеңберінің доғасы болып келсе (15 а, сур), онда түр өзгеру ошағы у, z координаталары аталған параметрлердің сәйкесінше қатынастарымен байланысты екі параметрлі бетпен көрсетіледі:

Z = R(x)[1-cos{L/R(x)}; Y = R(x)sin{L/R(x)}. (1)

Егер, х = const қимасы ауыспалы қисықтықтың доғасы (көпрадиусты қалыпқа келтіру) болып келе, онда түр өзгерудің ошағы у, z координаталары аталған параметрлердің сәйкесінше қатынастарымен байланысты көп параметрлік бет болады.

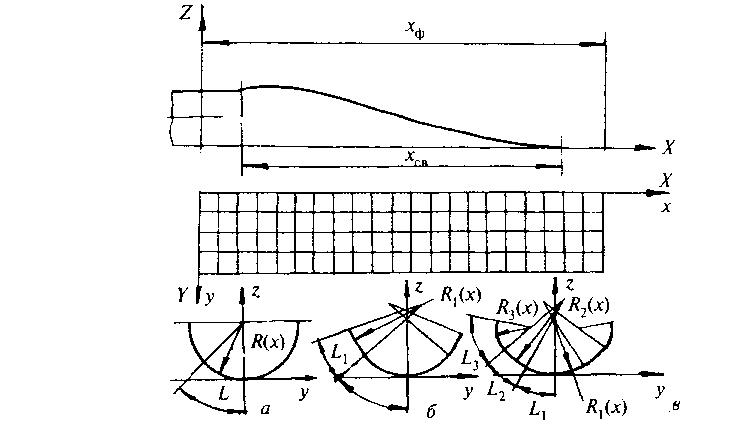
15 сурет – Бұрғылаудың біррадиусты (а), екірадиусты (б) және үшрадиусты (в) сызбасы үшін құбырлы дайындаманың түр өзгеруінің ошағы

Екірадиусты мөлшерлеу жағдайы үшін х = const жолағының қимасы екі радиусты доға болып келеді, және де L₁ учаскесінде - радиусының доғасы, (L-L₁) учаскесінде —R₂(х) радиусының доғасы, мұнда L — екірадиусты доға бойынша ағымдық ұзындық (15 б, сур).

Осыдан шығып, қалыпқа келтірудің екі радиусты сызбасы үшін түр өзгеру ошағы Z, Y координаталары L < L₁ кезінде және L параметрлерімен (12.2) теңдеулерімен байланысты төртпараметрлік бет болады, ал L > L₁ кезінде төмендегі қатынастармен

(2)

Үшрадиусты мөлшерлеулеудің жағдайы үшін х = const жолағының қимасы үшрадиусты доға болып келеді, (сур. 15, в), және де учаскесінде — радиусты доға, L₂ келесі бөлімшесінде—R₂(x) радиусты доға, учаскесінде—R₃(х) радиусты доға, мұнда L — үшрадиусты доға бойынша ағымдық ұзындық.

Нәтижесінде қалыпқа келтірудің үш радиусты сызбасы үшін алты параметрлік бетті аламыз, оның X, Y координаталары келесі қатынастармен байланысты: L ≤ — (15) кезінде R₁(x) және L, - (16) кезінде R₂(x) және L үшін, ал L > L₁ + L₂ кезінде R₃(x) және L үшін:

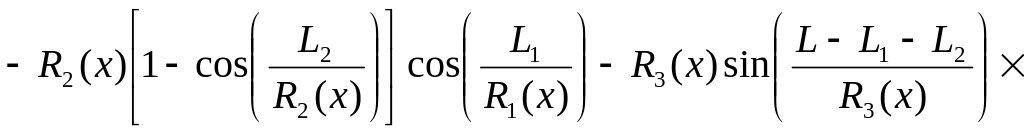
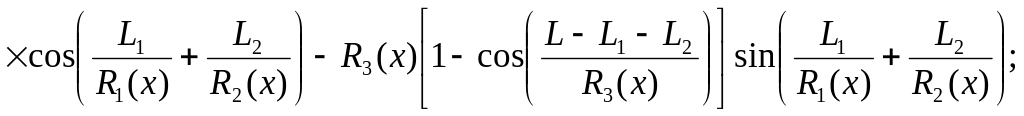
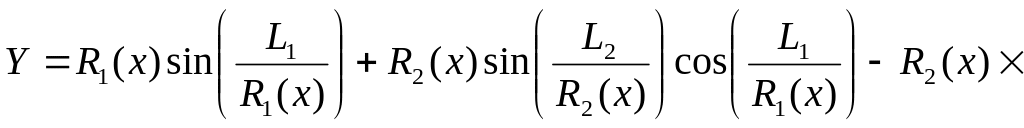
(3)

мұнда , ( және — қалыптасатын жолақтың нүктелерінің лагранжды координаталарының белгісіздері); және — жолақтың орта жазықтығының туынды материалдық нүктесінің түр өзгеру ошағының орта бетінің геометриялық нүктесінің сәйкестік заңы.