Задание

1. Написать программу, реализующую алгоритм шифрования стандартом DES файлов любого типа.

Выполнение

Окно работы программы представлено на рис. 5.

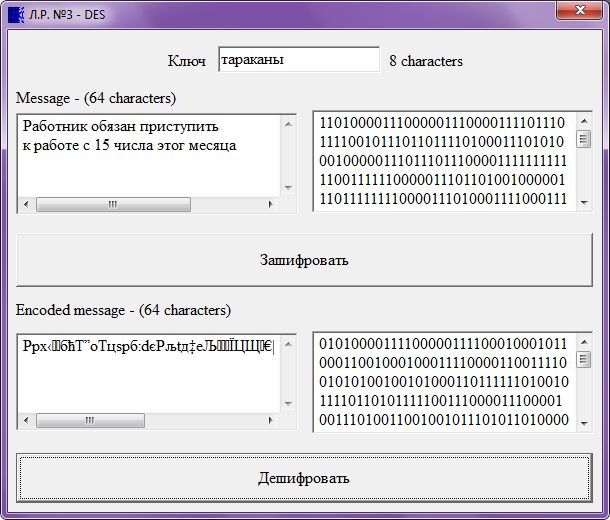
Рис. 5. Реализация шифрования алгоритмом DES

В поле «Ключ» вводим ключевое слово, затем в поле «Message» - текст, который требуется зашифровать. Нажав кнопку «Зашифровать», получаем в поле «Encoded message» зашифрованный текст. С помощью кнопки «Дешифровать» можно произвести дешифрование.

Листинг программы представлен в Приложении 3.

Вывод: в ходе выполнения данной лабораторной работы был изучен алгоритм шифрования DES.

Лабораторная работа №4

Схема шифрования Эль Гамаля

Цель работы: формирование навыков использования схемы шифрования Эль Гамаля.

Теоретическая часть

Схема Эль Гамаля, предложенная в 1985 г. может быть использована как для шифрования, так и для цифровых подписей. Безопасность схемы Эль Гамаля обусловлена сложностью вычисления дискретных алгоритмов в конечном поле.

Для генерации пары ключей сначала берется простое число Р и два случайных числа G и X, каждое из которых меньше Р. Затем вычисляется:

Y = G^x mod P

Общедоступными ключами являются Y, G и Р, а секретным ключом является X.

Для подписи сообщения М выбирается случайное число К, которое является простым по отношению к Р-1.

После этого вычисляется а = G^k mod P.

Далее находим b = Y^k *M mod Р. Электронной подписью для сообщения М будет служить пара а и b. Случайное число k следует хранить в секрете. Для верификации подписи необходимо проверить равенство:

Пара а и b представляют собой зашифрованный текст. Следует заметить, что зашифрованный текст имеет размер в два раза больше исходного. Для дешифрования производится вычисление: М = b/a^x mod P

Пример. Выберем Р = 11, G = 2, секретный ключ X = 8. Вычисляем:

Y = G^x mod Р = 2⁸ mod 11 = 256 mod 11=3.

Итак, открытый ключ Y = 3.

Пусть сообщение М = 5. Выберем некоторое случайное число К = 9. Убедимся, что НОД(К, Р-1) = 1. Действительно, НОД(9, 10) = 1. Вычисляем пару чисел а, b:

а = G^k mod P = Т mod 11 = 512 mod 11=6.

b = Y^k*M mod P = 3⁹*5 mod 11 = 19683* 5 mod 11 =9.

Получим шифртекст (a, b) = (6, 9).

Выполним расшифрование этого шифртекста. Вычисляем сообщение М, используя секретный ключ X:

М = b/a^x mod Р = 9/6⁸ mod 11.

Выражение М = 9/6⁸ mod 11 можно представить в виде

б⁸*M = 9mod 11

или

1679616* М = 9 mod 11.

Решая данное сравнение, получим, M=5.

В реальных схемах шифрования необходимо использовать в качестве модуля P большое целое простое число, имеющее в двоичном представлении длину 512 … 1024 бит.

Задание

• Написать программу, реализующую схему шифрования Эль Гамаля.

Выполнение

Окно работы программы показано на рис.6.

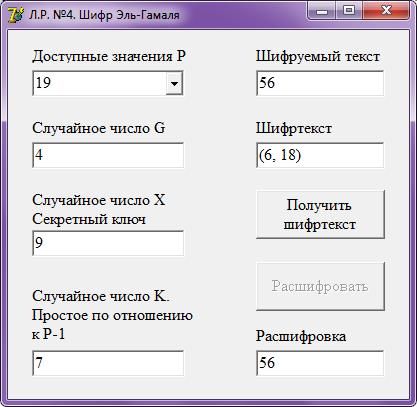
Рис. 6. Реализация алгоритмом Эль-Гамаля

В полях «Доступные значения Р», «Случайное число G», «Случайное число Х», «Случайное число К» и «Шифруемый текст» вводим нужные параметры. Нажав кнопку «Получить шифртекст», получаем зашифрованное значение в поле «Шифртекст». С помощью кнопки «Расшифровать» в поле «Расшифровка» получаем исходный шифруемый текст.

Листинг программы приведен в Приложение 4.

Вывод: в ходе выполнения данной лабораторной работы был изучен алгоритм шифрования Эль-Гамаля.