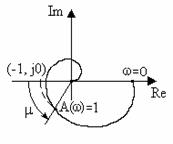
40. Что такое «запасы устойчивости по фазе и по амплитуде»?

Запас устойчивости по амплитуде задается некоторой величиной h (рис.5.12,а), на которую должен отличаться модуль АФЧХ разомкнутой системы от единицы на частоте, при которой фаза равняется -1800, т.е.

.                     (5.14)

                         а)                                                б)

Рис. 5.12. АФЧХ разомкнутой системы

Запас устойчивости по фазе задается некоторым углом  (рис.5.12,б), на который должна отличаться фаза АФЧХ разомкнутой системы от -1800 на частоте, при которой модуль равняется единице, т.е.

.                         (5.15)

В хорошо демпфированных системах запас устойчивости по амплитуде составляет примерно 620 дб, что составляет 210 в линейном масштабе, а запас по фазе  30600. 

Чтобы спроектировать систему с заданными запасами устойчивости по модулю hз и фазе з, строят запретную область вокруг точки с координатами (-1, j0), в которую не должна заходить АФЧХ разомкнутой системы (рис.5.13).

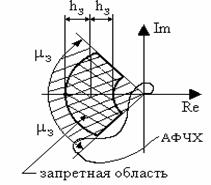
Рис. 5.13. Запретная область для АФЧХ разомкнутой системы

Nursultan

41. Какие различные формы имеет функция plot?

Функция plot имеет различные формы, связанные с входными параметрами, например plot(y) создает кусочно-линейный график зависимости элементов y от их индексов. Если в качестве аргументов заданы два вектора, то plot(x,y) создаст график зависимости y от x. Например, для построения графика функции sin в интервале от 0 до 2p, сделаем следующее. Программа построила график зависимости, который отображается в окне Figure 1. MatLab автоматически присваивает каждому графику свой цвет (исключая случаи, когда это делает пользователь), что позволяет различать наборы данных. Команда hold on позволяет добавлять кривые на существующий график. Функция subplot позволяет выводить множество графиков в одном окне. Рассмотрение возможностей MatLab по визуализации данных начнем с двумерных графиков, которые обычно строятся с помощью функции plot(). Множество вариантов работы данной функции лучше всего рассмотреть на конкретных примерах. Предположим, что требуется вывести график функции синуса в диапазоне от 0 до pi. Для этого зададим вектор (множество) точек по оси Ox, в которых будут отображаться значения функции синуса: x = 0:0.01:pi; В результате получится вектор столбец со множеством значений от 0 до pi и с шагом 0,01. Затем, вычислим множество значений функции синуса в этих точках: y = sin(x); и выведем результат на экран plot(x,y); Представленная запись функции plot() показывает, что сначала записывается аргумент со множеством точек оси Ох, а затем, аргумент со множеством точек оси Oy. Зная эти значения, функция plot() имеет возможность построить точки на плоскости и линейно их интерполировать для придания непрерывного вида графика.

42. Какая функция позволяет выводить множество графиков в одном окне?

Функция subplot позволяет выводить множество графиков в одном окне. Данная команда выполняется перед обращением к функциям построения графиков для одновременной выдачи нескольких графиков в различных частях графического окна. Команды subplot(mnp) или subplot(m, n, p), где mnp - 3 цифры, производит разбивку графического окна на несколько подокон, создавая при этом новые объекты axes; значение m указывает, на сколько частей разбивается окно по горизонтали, n - по вертикали, а p - номер подокна, куда будет выводиться очередной график. Эти же команды могут использоваться для перехода от одного подокна к другому. Команда subplot(h), где h - дескриптор для объекта axes соответствующего подокна, - другой способ выбора подокна для размещения графика. Команды clf, subplot(111), subplot(1, 1, 1) выполняют одну и ту же функцию - удаляют все подокна и возвращают графическое окно в штатное состояние. Пример: В верхней части экрана строится функция y1 = sin(x), в нижней - y2 = log(abs(y)). x = -1:.1:1; y1 = sin(x); subplot(2, 1, 1), plot(x, y1) y2 = log(abs(y1)); subplot(2, 1, 2), plot(x, y2).

43. Какая команда позволяет добавлять кривые на существующий график? Команда hold on позволяет добавлять кривые на существующий график. Команда hold on включает режим сохранения текущего графика и свойств объекта axes, так что последующие команды приведут к добавлению новых графиков в графическом окне.Команда hold off выключает режим сохранения графика. Команда hold реализует переключение от одного режима к другому. Команды hold воздействуют на значения свойства NextPlot объектов figure и axes: hold on присваивает свойству NextPlot для текущих объектов figure и axes значение add;

hold off присваивает свойству NextPlot для текущих объектов figure и axes значение replace.