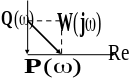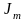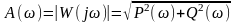Методы определения амплитудно-частотных характеристик

1. Экспериментальный:

• На вход системы (звена) подаётся гармонический синусоидальный сигнал постоянной амплитуды , частота 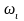которого изменяется в заданном диапазоне;

• Для каждой частоты измеряются амплитуды 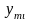выходного сигнала.

• Находят соотношение ;

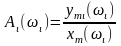• Изменяя частоту от нуля до наибольшего значения, строят графики - ;

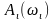2. Аналитический:

• Определяют передаточную функцию системы (звена) W(p);

• Заменяют в выражении ПФ оператор р на ,

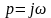• получают комплексную амплитудно-фазовую частотную характеристику (комплексный коэффициент передачи) системы (звена)

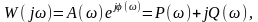
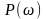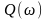Где - вещественная частотная характеристика;

- мнимая частотная характеристика.

Эти характеристики не имеют физического смысла и не могут быть получены экспериментально, но они используются для определения амплитудно-частотной характеристики .

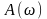На комплексной плоскости комплексная частотная характеристика представляется вектором

Амплитудно-частотная характеристика:

35. Построенная в логарифмическом масштабе АЧХ, называется логарифмической амплитудной частотной характеристикой (ЛАЧХ)

,

(2.43)

Эта величина выражается в децибелах (дб). При изображении ЛАЧХ удобнее по оси абсцисс откладывать частоту в логарифмическом масштабе, то есть  , выраженную в декадах (дек).

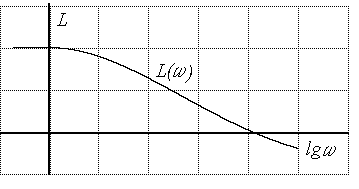
Логарифмическая амплитудно-частотная характеристика имеет начальный наклон - 12 дб / октаеа.

ЛФЧХ - это зависимость фазы выходного сигнала от частоты в полулогарифмическом масштабе

• по оси абсцисс откладывается частота в логарифмическом масштабе (в декадах или октавах)

• по оси ординат откладывается выходная фаза в угловых градусах или радианах.

Неперы и октавы в настоящее время являются устаревшими и практически не используются. Причины построения амплитудных и фазных характеристик в логарифмическом масштабе - возможность исследования характеристик в большом диапазоне.

Построение асимптотической ЛФЧХ (аппроксимация)[править | править исходный текст]

Для построения аппроксимированной ФЧХ используют запись передаточной функции в том же виде, что и для ЛАЧХ:

Основной принцип построения ФЧХ — начертить отдельные графики для каждого полюса или нуля, затем сложив их. Точная кривая фазо-частотной характеристики задаётся уравнением:

2. 37. Способы построения частотных характеристик в MATLAB.

Частотная характеристика определяется как реакция системы на комплексный экспоненциальный сигнал 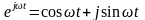. Для ее построения надо использовать подстановку в передаточной функции 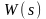. Выражение называется частотной передаточной функцией или амплитудно-фазовой частотной характеристикой системы (АФЧХ).

Зависимость модуля величины от частоты называется амплитудной частотной характеристикой (АЧХ), а зависимость аргумента комплексного числа (фазы) от частоты ­– фазовой частотной характеристикой (ФЧХ):

.

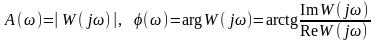АЧХ показывает, насколько усиливается амплитуда сигналов разных частот после прохождения через систему, а ФЧХ характеризует сдвиг фазы сигнала.

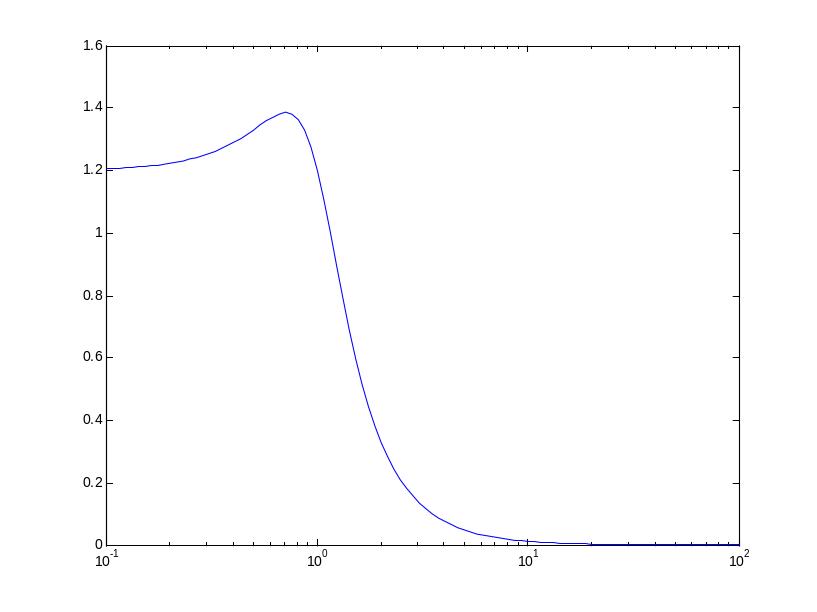
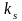
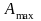
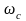
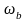
Реальные объекты имеют строго правильную передаточную функцию, поэтому их АЧХ убывает с ростом частоты и асимптотически стремится к нулю. Говорят, что такой объект обладает свойством фильтра – фильтрует (не пропускает) высокочастотные сигналы (помехи, шумы измерений). Это свойство служит основой для использования метода гармонического баланса.

Частота, после которой значение АЧХ уменьшается ниже 0 дБ (коэффициент усиления меньше 1, сигнал ослабляется), называется частотой среза системы 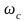.Частота, после которой значение АЧХ падает ниже -3 дБ (коэффициент усиления меньше, чем 0.708), называется полосой пропускания системы . Для ее вычисления используют команду

>> b = bandwidth ( f )

Максимум АЧХ соответствует частоте, на которой усиление наибольшее. Значение АЧХ при 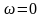равно усилению при постоянном сигнале, то есть, статическому коэффициенту усиления . Это следует и из равенства

Чтобы построить частотные характеристики в Matlab, надо сначала создать массив частот в нужном диапазоне. Для этого можно использовать функции linspace (равномерное распределение точек по линейной шкале) и logspace (равномерное распределение точек по логарифмической шкале). Команда

>> w = linspace (0, 10, 100);

строит массив из 100 точек с равномерным шагом в интервале от 0 до 10, а команда

>> w = logspace (-1, 2, 100);

– массив из 100 точек с равномерным шагом по логарифмической шкале в интервале от 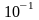до .

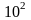Частотная характеристика на сетке w для линейной модели f (заданной как передаточная функция, модель в пространстве состояний или в форме «нули-полюса») вычисляется с помощью функции freqresp:

>> r = freqresp(f, w);

Функция freqresp возвращает трехмерный массив. Это связано с тем, что она применима и для многомерных моделей (с несколькими входами и выходами), передаточная функция которых представляет собой матрицу. Первые два индекса обозначают строку и столбец в этой матрице, а третий – номер точки частотной характеристики. Для системы с одним входом и одним выходом удобно преобразовать трехмерный массив в одномерный командой

>> r = r(:);

Для вывода графика АЧХ на экран можно использовать команды Matlab

>> plot ( w, abs(r) );

>> semilogx ( w, abs(r) );

>> loglog ( w, abs(r) );

В первом случае масштаб обеих осей координат – линейный, во втором случае используется логарифмический масштаб по оси абсцисс (частот), в последнем ­– логарифмический масштаб по обеим осям. Для вычисления фазы (в градусах) используется команда

>> phi = angle(r)*180/pi;

после чего можно строить ФЧХ, например:

>> semilogx ( w, phi );

З8. Сформулируйте критерий устойчивости Гурвица, укажите на необходимое условие устойчивости линейных САУ, вытекающее из этого критерия?

Критерий Гурвица: для того, чтобы САУ была устойчива, необходи-мо и достаточно, чтобы при всех положительных коэффициентах харак-теристического полинома определитель Гурвица и все его диагональные ми-норы были положительными.

САУ будет находиться на границе устойчивости, если при выполнении всех перечисленных условий минор  n-1 = 0 (граница колебательной устой-чивости) или а n = 0 (граница апериодической устойчивости). Этот критерий позволяет исследовать также влияние изменения какого-либо параметра САУ на ее устойчивость, однако из-за сложности вычислительных процедур, ко-торая возрастает с увеличением порядка полинома, критерий Гурвица не применяют для систем выше четвертого порядка.

39. Сформулируйте критерий Найквиста для случая САУ, устойчивых в разомкнутом состоянии, а также для астатических САУ.

Критерий Найквиста: если в разомкнутом состоянии САУ устойчи- ва, то для того, чтобы она была устойчива в замкнутом состоянии, необхо- димо и достаточно, чтобы АФЧХ ее разомкнутого контура не охватывала точку с координатами (–1, j0).

Главной отличительной особенностью этого критерия является воз- можность исследования устойчивости замкнутой САУ по виду АФЧХ ее разомкнутого контура, которую строить гораздо проще. Кроме того, крите- рий Найквиста позволяет определять устойчивость по экспериментально сня- тым частотным характеристикам системы.

Этот критерий позволяет легко определять запас устойчивости по ам- плитуде и по фазе. Обычно рекомендуется выбирать следующие значения: А  ;  300.

Критерий Найквиста удобно применять для исследования систем с за- паздыванием. Частотную передаточную функцию разомкнутого контура можно привести к виду

W j W j e j ( ) ( ) ,       0

где W0(j) – частотная передаточная функция всех звеньев САУ, за исключе- нием звена чистого запаздывания.

Если разомкнутая САУ представляет собой последовательное соедине- ние ТДЗ, то для исследования устойчивости удобно применять логарифмиче- ские частотные характеристики. В этом случае формулировка критерия Най- квиста для случая устойчивой разомкнутой САУ следующая: замкнутая САУ будет устойчивой, если ЛАХ ее разомкнутого контура пересечет ось ча- стот раньше, чем ЛФХ достигнет значения (–). Часто эту разновидность критерия Найквиста называют критерием ЛЧХ. 17