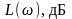15.Назовите два способа запуска пакета Simulink ?

3. Запустить Simulink из среды MATLAB.

Обычно Simulink запускается соответствующей кнопкой из панели инструментов,

что было описано в задании 2, после чего все последующие действия выполняются в сре-

де MATLAB + Simulink. Можно также запустить Simulink, выполнив в командной строке

MATLAB команду

>> simulink Для запуска пакета Simulink щелкните по кнопке в командном окне Matlab или введите команду simulink в командной строке.

13.Возможности моделирования, предоставляемые пакетом прикладных программ Control System Toolbox (сst) и matlab Simulink.

Для проведения исследований и проектирования систем управления в состав системы MATLAB включены несколько ППП, предоставляющих широкий набор проблемно-ориентированных инструментальных средств. Одним из таких пакетов является ППП Control System Toolbox, который содержит комплекс программ, реализующих специальные методы теории управления, предназначенные для анализа и синтеза линейных непрерывных и дискретных стационарных систем управления. Пакет реализован с привлечением принципов объектно-ориентированного программирования, в соответствии с которыми все процедуры в ППП производятся с представителями специально введенного класса объектов – LTI-объектов, определяющих линейные системы с постоянными параметрами [1]. Особую роль для специалистов в области теории управления, обращающихся в своих исследованиях к инструментарию среды MATLAB, играет подсистема Simulink – компонента MATLAB, представляющая собой удобное и эффективное средство компьютерного и имитационного моделирования динамических процессов. 

14.Основные этапы работы с программой.

Программный код Matlab, основные этапы и особенности его разработки. Принципы работы со скриптами и функциями, их структура. Типы и функциональные возможности комментариев. Входные и выходные параметры. Создание p-кода. Вывод данных в командное окно.

16.Назовите основные разделы Simulink?

Simulink является достаточно самостоятельным инструментом MATLAB и при работе с ним совсем не требуется знать сам MATLAB и остальные его приложения. С другой стороны доступ к функциям MATLAB и другим его инструментам остается открытым и их можно использовать в Simulink. Часть входящих в состав пакетов имеет инструменты, встраиваемые в Simulink (например, LTI-Viewer приложения Control System Toolbox – пакета для разработки систем управления). Имеются также дополнительные библиотеки блоков для разных областей применения (например, Power System Blockset – моделирование электротехнических устройств, Digital Signal Processing Blockset – набор блоков для разработки цифровых устройств и т.д).

Библиотека Simulink содержит следующие основные разделы:

1. Continuous – библиотека непрерывных элементов (интегратор, дифференциатор, линейная система ОДУ и т.д.);

2. Discrete – библиотека дискретных элементов (интегратор с дискретным временем, дискретный фильтр и т.д.);

3. Functions & Tables – функции и таблицы (вызов функций Matlab, S-функции, блок, отображающий входной вектор в выходной (с использованием линейной интерполяции значений, определенных в параметрах блока) и т.д.);

4. Math – математические функции (абсолютное значение, комбинаторная логика, выделение вещественной и мнимой составляющей комплексного числа и т.д.);

5. Nonlinear – нелинейные элементы (релейное звено, переключатель и т.д. );

6. Signals & Systems – сигналы и системы (составной блок, входной сигнал, выходной сигнал, мультиплексер, демультиплексер и т.д.);

7. Sinks – средства отображения (временная диаграмма, вывод результатов в файл, остановка выполнения модели и т.д.);

8. Sources – источники сигналов (генератор импульсных/синусоидальных сигналов, генератор случайных чисел, генератор пилообразных сигналов, часы и т.д.).

9. Subsystems – блоки подсистем.

и цифровых устройств и т.д).

Batondiki kop kiskartindar

17.Математическая модель

Математи́ческая моде́ль — это математическое представление реальности[1]. Является частным случаем понятия модели, как системы, исследование которой позволяет получать информацию о некоторой другой системе.

Процесс построения и изучения математических моделей называется математическим моделированием.

Все естественные и общественные науки, использующие математический аппарат, по сути занимаются математическим моделированием: заменяют объект его математической моделью и затем изучают последнюю. Связь математической модели с реальностью осуществляется с помощью цепочки гипотез, идеализаций и упрощений. С помощью математических методов описывается, как правило, идеальный объект, построенный на этапе содержательного моделирования

Определения

Никакое определение не может в полном объёме охватить реально существующую деятельность по математическому моделированию. Несмотря на это, определения полезны тем, что в них делается попытка выделить наиболее существенные черты.

• Определение модели по А. А. Ляпунову: Моделирование — это опосредованное практическое или теоретическое исследование объекта, при котором непосредственно изучается не сам интересующий нас объект, а некоторая вспомогательная искусственная или естественная система (модель):

1. находящаяся в некотором объективном соответствии с познаваемым объектом;

2. способная замещать его в определенных отношениях;

3. дающая при её исследовании, в конечном счете, информацию о самом моделируемом объекте.[2]

• По учебнику Советова и Яковлева [3]: «модель (лат. modulus — мера) — это объект-заместитель объекта-оригинала, обеспечивающий изучение некоторых свойстворигинала». (с. 6) «Замещение одного объекта другим с целью получения информации о важнейших свойствах объекта-оригинала с помощью объекта-модели называется моделированием». (с. 6) «Под математическим моделированием будем понимать процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью, и исследование этой модели, позволяющее получать характеристики рассматриваемого реального объекта. Вид математической модели зависит как от природы реального объекта, так и от задач исследования объекта и требуемойдостоверности и точности решения этой задачи».

• По Самарскому и Михайлову [4], математическая модель — это «„эквивалент“ объекта, отражающий в математической форме важнейшие его свойства — законы, которым он подчиняется, связи, присущие составляющим его частям, и т.д.» Существует в триадах «модель-алгоритм-программа». «Создав триаду „модель-алгоритм-программа“, исследователь получает в руки универсальный, гибкий и недорогой инструмент, который вначале отлаживается, тестируется в пробных вычислительных экспериментах. После того, как адекватность (достаточное соответствие) триады исходному объекту установлена, с моделью проводятся разнообразные и подробные „опыты“, дающие все требуемые качественные и количественные свойства и характеристики объекта». (с.7-8)

• По монографии Мышкиса [5]: «Перейдем к общему определению. Пусть мы собираемся исследовать некоторую совокупность свойств реального объекта с помощью математики (здесь термин объект понимается в наиболее широком смысле: объектом может служить не только то, что обычно именуется этим словом, но и любая ситуация, явление, процесс и т.д.). Для этого мы выбираем (как говорят, строим) „математический объект“ — систему уравнений, или арифметических соотношений, или геометрических фигур, или комбинацию того и другого и т.д.,— исследование которого средствами математики и должно ответить на поставленные вопросы о свойствах . В этих условиях называется математической моделью объекта относительно совокупности его свойств». (с.8)

• По Севостьянову А. Г.[6] : «Математической моделью называется совокупность математических соотношений, уравнений, неравенств и т.п., описывающих основные закономерности, присущие изучаемому процессу, объекту или системе».

• Несколько менее общее определение математической модели, основанное на идеализации «вход — выход — состояние», заимствованной из теории автоматов, даёт Wiktionary: «Абстрактное математическое представление процесса, устройства или теоретической идеи; оно использует набор переменных, чтобы представлять входы, выходы и внутренние состояния, а также множества уравнений и неравенств для описания их взаимодействия».[7]

• Наконец, наиболее лаконичное определение математической модели: «Уравнение, выражающее идею».[8]

Классификация моделей

Формальная классификация моделей

Формальная классификация моделей основывается на классификации используемых математических средств. Часто строится в форме дихотомий. Например, один из популярных наборов дихотомий [9]:

• Линейные или нелинейные модели[10];

• Сосредоточенные или распределённые системы[11];

• Детерминированные или стохастические[12];

• Статические или динамические[12];

• Дискретные или непрерывные [12].

и так далее. Каждая построенная модель является линейной или нелинейной, детерминированной или стохастической, … Естественно, что возможны и смешанные типы: в одном отношении сосредоточенные (по части параметров), в другом — распределённые модели и т.д.

Классификация по способу представления объекта

Наряду с формальной классификацией, модели различаются по способу представления объекта:

• Структурные или функциональные модели

Структурные модели представляют объект как систему со своим устройством и механизмом функционирования. Функциональные модели не используют таких представлений и отражают только внешне воспринимаемое поведение (функционирование) объекта. В их предельном выражении они называются также моделями«чёрного ящика».[13] Возможны также комбинированные типы моделей, которые иногда называют моделями «серого ящика».

Содержательные и формальные модели

Практически все авторы, описывающие процесс математического моделирования, указывают, что сначала строится особая идеальная конструкция, содержательная модель[14]. Устоявшейся терминологии здесь нет, и другие авторы называют этот идеальный объект концептуальная модель[15], умозрительная модель[16] илипредмодель[17]. При этом финальная математическая конструкция называется формальной моделью или просто математической моделью, полученной в результате формализации данной содержательной модели (предмодели). Построение содержательной модели может производиться с помощью набора готовых идеализаций, как в механике, где идеальные пружины, твёрдые тела, идеальные маятники, упругие среды и т.п. дают готовые структурные элементы для содержательного моделирования. Однако в областях знания, где не существует полностью завершенных формализованных теорий (передний край физики, биологии, экономики,социологии, психологии, и большинства других областей), создание содержательных моделей резко усложняется.

Содержательная классификация моделей

В работе Р. Пайерлса[18] дана классификация математических моделей, используемых в физике и, шире, в естественных науках. В книге А. Н. Горбаня и Р. Г. Хлебопроса[19] эта классификация проанализирована и расширена. Эта классификация сфокусирована, в первую очередь, на этапе построения содержательной модели.

Тип 1: Гипотеза (такое могло бы быть)

Эти модели «представляют собой пробное описание явления, причем автор либо верит в его возможность, либо считает даже его истинным». По Р. Пайерлсу это, например, модель Солнечной системы по Птолемею и модель Коперника (усовершенствованная Кеплером), модель атома Резерфорда и модель Большого Взрыва.

Никакая гипотеза в науке не бывает доказана раз и навсегда. Очень чётко это сформулировал Ричард Фейнман:

«У нас всегда есть возможность опровергнуть теорию, но, обратите внимание, мы никогда не можем доказать, что она правильна. Предположим, что вы выдвинули удачную гипотезу, рассчитали, к чему это ведет, и выяснили, что все ее следствия подтверждаются экспериментально. Значит ли это, что ваша теория правильна? Нет, просто-напросто это значит, что вам не удалось ее опровергнуть».[20]

Если модель первого типа построена, то это означает, что она временно признаётся за истину и можно сконцентрироваться на других проблемах. Однако это не может быть точкой в исследованиях, но только вре́менной паузой: статус модели первого типа может быть только вре́менным.

Тип 2: Феноменологическая модель (ведем себя так, как если бы…)

Феноменологическая модель содержит механизм для описания явления, хотя этот механизм недостаточно убедителен, не может быть достаточно подтверждён имеющимися данными или плохо согласуется с имеющимися теориями и накопленным знанием об объекте. Поэтому феноменологические модели имеют статус вре́менных решений. Считается, что ответ всё ещё неизвестен, и необходимо продолжить поиск «истинных механизмов». Ко второму типу Пайерлс относит, например, модели теплорода и кварковую модель элементарных частиц.

Роль модели в исследовании может меняться со временем, может случиться так, что новые данные и теории подтвердят феноменологические модели и те будут повышены до статуса гипотезы. Аналогично новое знание может постепенно прийти в противоречие с моделями-гипотезами первого типа, и те могут быть переведены во второй. Так, кварковая модель постепенно переходит в разряд гипотез; атомизм в физике возник как временное решение, но с ходом истории перешёл в первый тип. А вот модели эфира проделали путь от типа 1 к типу 2, а сейчас находятся вне науки.

Идея упрощения очень популярна при построении моделей. Но упрощение бывает разным. Пайерлс выделяет три типа упрощений в моделировании.

Тип 3: Приближение (что-то считаем очень большим или очень малым)

Если можно построить уравнения, описывающие исследуемую систему, то это не значит, что их можно решить даже с помощью компьютера. Общепринятый прием в этом случае — использование приближений (моделей типа 3). Среди них модели линейного отклика. Уравнения заменяются линейными. Стандартный пример —закон Ома.

Если мы используем модель идеального газа для описания достаточно разреженных газов, то это — модель типа 3 (приближение). При более высоких плотностях газа тоже полезно представлять себе более простую ситуацию с идеальным газом для качественного понимания и оценок, но тогда это уже тип 4.

Тип 4: Упрощение (опустим для ясности некоторые детали)

В модели типа 4 отбрасываются детали, которые могут заметно и не всегда контролируемо повлиять на результат. Одни и те же уравнения могут служить моделью типа 3 (приближение) или 4 (опустим для ясности некоторые детали) — это зависит от явления, для изучения которого используется модель. Так, если модели линейного отклика применяются при отсутствии более сложных моделей (то есть не производится линеаризация нелинейных уравнений, а просто ищутся линейные уравнения, описывающие объект), то это уже феноменологические линейные модели, и относятся они к следующему типу 4 (все нелинейные детали «для ясности» опускаем).

Примеры: применение модели идеального газа к неидеальному, уравнение состояния Ван-дер-Ваальса, большинство моделей физики твердого тела, жидкостей иядерной физики. Путь от микроописания к свойствам тел (или сред), состоящих из большого числа частиц, очень длинен. Приходится отбрасывать многие детали. Это приводит к моделям 4-го типа.

Тип 5: Эвристическая модель (количественного подтверждения нет, но модель способствует более глубокому проникновению в суть дела)

Эвристическая модель сохраняет лишь качественное подобие реальности и даёт предсказания только «по порядку величины». Типичный пример — приближение средней длины свободного пробега в кинетической теории. Оно даёт простые формулы для коэффициентов вязкости, диффузии, теплопроводности, согласующиеся с реальностью по порядку величины.

Но при построении новой физики далеко не сразу получается модель, дающая хотя бы качественное описание объекта — модель пятого типа. В этом случае часто используют модель по аналогии, отражающую действительность хоть в какой-нибудь черте.

Тип 6: Аналогия (учтём только некоторые особенности)

Р. Пайерлс приводит историю использования аналогий в первой статье В. Гейзенберга о природе ядерных сил. «Это произошло после открытия нейтрона, и хотя сам В. Гейзенберг понимал, что можно описывать ядра состоящими из нейтронов и протонов, он не мог все же избавиться от мысли, что нейтрон должен, в конечном счете, состоять из протона и электрона. При этом возникала аналогия между взаимодействием в системе нейтрон — протон и взаимодействием атома водорода и протоном. Эта-то аналогия и привела его к заключению, что должны существовать обменные силы взаимодействия между нейтроном и протоном, которые аналогичны обменным силам в системе , обусловленным переходом электрона между двумя протонами. … Позднее было все-таки доказано существование обменных сил взаимодействия между нейтроном и протоном, хотя ими не исчерпывалось полностью взаимодействие между двумя частицами… Но, следуя все той же аналогии, В. Гейзенберг пришёл к заключению об отсутствии ядерных сил взаимодействия между двумя протонами и к постулированию отталкивания между двумя нейтронами. Оба последних вывода находятся в противоречии с данными более поздних исследований».

Тип 7: Мысленный эксперимент (главное состоит в опровержении возможности)

А. Эйнштейн был одним из великих мастеров мысленного эксперимента. Вот один из его экспериментов. Он был придуман в юности и, в конце концов, привел к построению специальной теории относительности. Предположим, что в классической физике мы движемся за световой волной со скоростью света. Мы будем наблюдать периодически меняющееся в пространстве и постоянное во времени электромагнитное поле. Согласно уравнениям Максвелла, этого быть не может. Отсюда юный Эйнштейн заключил: либо законы природы меняются при смене системы отсчета, либо скорость света не зависит от системы отсчета. Он выбрал второй — более красивый вариант. Другой знаменитый мысленный эксперимент Эйнштейна — Парадокс Эйнштейна — Подольского — Розена.

А вот и тип 8, широко распространенный в математических моделях биологических систем.

Тип 8: Демонстрация возможности (главное — показать внутреннюю непротиворечивость возможности)[править | править исходный текст]

Это тоже мысленные эксперименты с воображаемыми сущностями, демонстрирующие, что предполагаемое явление согласуется с базовыми принципами и внутренне непротиворечиво. В этом основное отличие от моделей типа 7, которые вскрывают скрытые противоречия.

Один из самых знаменитых таких экспериментов — геометрия Лобачевского. (Лобачевский называл её «воображаемой геометрией»). Другой пример — массовое производство формально—кинетических моделей химических и биологических колебаний, автоволн и др. Парадокс Эйнштейна — Подольского — Розена был задуман как модель 7 типа, для демонстрации противоречивости квантовой механики. Совершенно незапланированным образом он со временем превратился в модель 8 типа — демонстрацию возможности квантовой телепортации информации.

В основе содержательной классификации — этапы, предшествующие математическому анализу и вычислениям. Восемь типов моделей по Р. Пайерлсу суть восемь типов исследовательских позиций при моделировании.

Жёсткие и мягкие модели

Гармонический осциллятор — пример так называемой «жёсткой» модели. Она получена в результате сильной идеализации реальной физической системы. Свойства гармонического осциллятора качественно изменяются малыми возмущениями. Например, если добавить в правую часть малое слагаемое (трение) ( — некоторый малый параметр), то получим экспоненциально затухающие колебания, если изменить знак добавочного слагаемого то трение превратится в накачку и амплитуда колебаний будет экспоненциально возрастать.

Для решения вопроса о применимости жёсткой модели необходимо понять, насколько существенными являются факторы, которыми мы пренебрегли. Нужно исследовать мягкие модели, получающиеся малым возмущением жёсткой. Для гармонического осциллятора они могут задаваться, например, следующим уравнением:

Здесь — некоторая функция, в которой может учитываться сила трения или зависимость коэффициента жёсткости пружины от степени её растяжения. Явный вид функции нас в данный момент не интересует.

Если мы докажем, что поведение мягкой модели принципиально не отличается от поведения жёсткой (вне зависимости от явного вида возмущающих факторов, если они достаточно малы), задача сведется к исследованию жёсткой модели. В противном случае применение результатов, полученных при изучении жёсткой модели, потребует дополнительных исследований.

Если система сохраняет свое качественное поведение при малом возмущении, говорят, что она структурно устойчива. Гармонический осциллятор — пример структурно-неустойчивой (негрубой) системы.[21] Тем не менее, эту модель можно применять для изучения процессов на ограниченных промежутках времени.

Универсальность моделей

Важнейшие математические модели обычно обладают важным свойством универсальности: принципиально разные реальные явления могут описываться одной и той же математической моделью. Скажем, гармонический осциллятор описывает не только поведение груза на пружине, но и другие колебательные процессы, зачастую имеющие совершенно иную природу: малые колебания маятника, колебания уровня жидкости в -образном сосуде или изменение силы тока в колебательном контуре. Таким образом, изучая одну математическую модель, мы изучаем сразу целый класс описываемых ею явлений. Именно этот изоморфизм законов, выражаемых математическими моделями в различных сегментах научного знания, подвиг Людвига фон Берталанфи на создание «Общей теории систем».

Прямая и обратная задачи математического моделирования

Существует множество задач, связанных с математическим моделированием. Во-первых, надо придумать основную схему моделируемого объекта, воспроизвести его в рамках идеализаций данной науки. Так, вагон поезда превращается в систему пластин и более сложных тел из разных материалов, каждый материал задается как его стандартная механическая идеализация (плотность, модули упругости, стандартные прочностные характеристики), после чего составляются уравнения, по дороге какие-то детали отбрасываются как несущественные, производятся расчёты, сравниваются с измерениями, модель уточняется, и так далее. Однако для разработки технологий математического моделирования полезно разобрать этот процесс на основные составные элементы.

Традиционно выделяют два основных класса задач, связанных с математическими моделями: прямые и обратные.

Прямая задача: структура модели и все её параметры считаются известными, главная задача — провести исследование модели для извлечения полезного знания об объекте. Какую статическую нагрузку выдержит мост? Как он будет реагировать на динамическую нагрузку (например, на марш роты солдат, или на прохождение поезда на различной скорости), как самолёт преодолеет звуковой барьер, не развалится ли он от флаттера, — вот типичные примеры прямой задачи. Постановка правильной прямой задачи (задание правильного вопроса) требует специального мастерства. Если не заданы правильные вопросы, то мост может обрушиться, даже если была построена хорошая модель для его поведения. Так, в 1879 г. в Великобритании обрушился металлический мост через реку Тей, конструкторы которого построили модель моста, рассчитали его на 20-кратный запас прочности на действие полезной нагрузки, но забыли о постоянно дующих в тех местах ветрах. И через полтора года он рухнул.[22]

В простейшем случае (одно уравнение осциллятора, например) прямая задача очень проста и сводится к явному решению этого уравнения.

Обратная задача: известно множество возможных моделей, надо выбрать конкретную модель на основании дополнительных данных об объекте. Чаще всего структура модели известна, и необходимо определить некоторые неизвестные параметры. Дополнительная информация может состоять в дополнительных эмпирических данных, или в требованиях к объекту (задача проектирования). Дополнительные данные могут поступать независимо от процесса решения обратной задачи (пассивное наблюдение) или быть результатом специально планируемого в ходе решения эксперимента (активное наблюдение).

Одним из первых примеров виртуозного решения обратной задачи с максимально полным использованием доступных данных был построенный И. Ньютоном метод восстановления сил трения по наблюдаемым затухающим колебаниям.

В качестве другого примера можно привести математическую статистику. Задача этой науки — разработка методов регистрации, описания и анализа данных наблюдений и экспериментов с целью построения вероятностных моделей массовых случайных явлений[23]. Т.е. множество возможных моделей ограничено вероятностными моделями. В конкретных задачах множество моделей ограничено сильнее.

Компьютерные системы моделирования

Для поддержки математического моделирования разработаны системы компьютерной математики, например, Maple, Mathematica, Mathcad, MATLAB, VisSim и др.[24]Они позволяют создавать формальные и блочные модели как простых, так и сложных процессов и устройств и легко менять параметры моделей в ходе моделирования. Блочные модели представлены блоками (чаще всего графическими), набор и соединение которых задаются диаграммой модели.

Дополнительные примеры

Модель Мальтуса

Скорость роста пропорциональна текущему размеру популяции. Она описывается дифференциальным уравнением

где — некоторый параметр, определяемый разностью между рождаемостью и смертностью. Решением этого уравнения является экспоненциальная функция . Если рождаемость превосходит смертность ( ), размер популяции неограниченно и очень быстро возрастает. Понятно, что в действительности этого не может происходить из-за ограниченности ресурсов. При достижении некоторого критического объёма популяции модель перестает быть адекватной, поскольку не учитывает ограниченность ресурсов. Уточнением модели Мальтуса может служить логистическая модель, которая описывается дифференциальным уравнением Ферхюльста

где — «равновесный» размер популяции, при котором рождаемость в точности компенсируется смертностью. Размер популяции в такой модели стремится к равновесному значению , причем такое поведение структурно устойчиво.

Система хищник-жертва[править | править исходный текст]

Основная статья: Система «хищник-жертва»

Допустим, что на некоторой территории обитают два вида животных: кролики (питающиеся растениями) и лисы (питающиеся кроликами). Пусть число кроликов , число лис . Используя модель Мальтуса с необходимыми поправками, учитывающими поедание кроликов лисами, приходим к следующей системе, носящей имямодели Лотки — Вольтерры:

Эта система имеет равновесное состояние, когда число кроликов и лис постоянно. Отклонение от этого состояния приводит к колебаниям численности кроликов и лис, аналогичным колебаниям гармонического осциллятора. Как и в случае гармонического осциллятора, это поведение не является структурно устойчивым: малое изменение модели (например, учитывающее ограниченность ресурсов, необходимых кроликам) может привести к качественному изменению поведения. Например, равновесное состояние может стать устойчивым, и колебания численности будут затухать. Возможна и противоположная ситуация, когда любое малое отклонение от положения равновесия приведет к катастрофическим последствиям, вплоть до полного вымирания одного из видов. На вопрос о том, какой из этих сценариев реализуется, модель Вольтерры — Лотки ответа не дает: здесь требуются дополнительные исследования.

18.Simulink

Советы пользователям Simulink от ведущего раздела

Полный список советов

12. Сохранение изображений схем и графиков в векторном формате

Для подготовки высококачественных документов содержащих схемы Simulink и графики, полученные с помощью Scope стандартных средств программы явно недостаточно. Пользователь фактически может лишь воспользоваться командой Edit\Copy model to clipboard для копирования схемы в буфер обменаWindows, а для копирования рисунка из блока Scope требуется использование комбинации клавиш Alt-Print Screen. При этом сами рисунки имеют растровый формат, что неудобно при создании документов с большими размерами страниц (например, плакатов), поскольку растровая структура рисунка становится видна. К тому же графики блока Scope имеют черный фон, что также не подходит для создания печатных документов.

Наилучшим выходом из такой ситуации является использование виртуального PDF-принтера, входящего в состав пакета Adobe Acrobat (речь идет о полном пакете, а не о широко распространенной программеAcrobat Reader, в состав которой виртуальный принтер не входит).

Для создания изображения схемы модели в векторном формате необходимо выполнить следующие операции:

1. Выполнить команду File\Print (воспользоваться ярлыком Print панели инструментов) окна модели.

2. После того, как окно Print Model откроется, необходимо выбрать Acrobat PDF Writer в качестве устройства печати и выполнить его настройку (кнопка Properties). Настройка PDF-принтера сводится к установке размера печатаемой страницы. Для сохранения исходных пропорций схемы необходимо выбрать размер страницы Custom и задать одинаковые величины ширины и высоты листа (например,297 mm на 297 mm). По завершении настройки принтера необходимо сохранить его установки клавишей OK и начать печать схемы (нажать клавишу OK в окне Print Model). После начала процесса печати на экран будет выведено окно диалога Save PDF File As, в котором необходимо задать имя файла рисунка и выбрать папку для его сохранения. По завершении печати в указанной папке появится файл рисунка с расширением PDF.

3. Полученный PDF-файл необходимо конвертировать в один из векторных форматов. Для этого можно воспользоваться, например, программой Adоbе Illustrator, также входящей в состав пакета Adobe Acrobat.

4. После того как PDF-файл рисунка будет открыт в программе Adоbе Illustrator необходимо установить нужные размеры листа рисунка (так, чтобы рисунок занимал весь лист), отредактировать рисунок (при необходимости) и сохранить его командой File\Export в одном из векторных форматов (например, EMF).

5. Выполнить вставку рисунка в текстовый документ командой Вставка\Риcунок\Из Файла...Результаты вставки рисунка показаны на рис. 1.

Рис.1. Схема модели в векторном формате

Для сравнения качества рисунка полученного по описанной методике и растрового рисунка на рис. 2 показан блок Sum, увеличенный в несколько раз. Качество фрагментов разительно отличается.

Рис.2. Фрагменты рисунка схемы в растровом (левый) и векторном (правый) форматах

Аналогичным образом выполняется создание векторного рисунка графиков из окна блока Scope. Предварительно, имеет смысл выполнить настройку графиков, введя в MATLAB команды (при открытом окне блока Scope):

set(0,'ShowHiddenHandles','On')

set(gcf,'menubar','figure')

и выполнить изменение толщины, типа линий и размера шрифта надписей. Так же может потребоваться изменение масштаба печатаемого рисунка в окне свойств PDF-принтера. Полученные по описанной методике графики показаны на рис. 3

19. Импульсная переходная функция (весовая функция, импульсная характеристика) — выходной сигналдинамической системы как реакция на входной сигнал в виде дельта-функции Дирака. В цифровых системах входной сигнал представляет собой простой импульс минимальной ширины (равной периоду дискретизации для дискретных систем) и максимальной амплитуды. В применении к фильтрации сигнала называется также ядром фильтра. Находит широкое применение в теории управления, обработке сигналов и изображений, теории связи и других областях инженерного дела.

Определение

Импульсной характеристикой системы называется её реакция на единичный импульс при нулевых начальных условиях.

Свойства

Выходной сигнал линейной системы может быть получен как свертка его входного сигнала и импульсной характеристики системы.

,

либо, в случае цифровой системы

.

Для того, чтобы система была физически реализуема в реальном времени, ее импульсная переходная функция должна удовлетворять условию: h(t)=0 при t<0. В противном случае система нереализуема, так как она нарушала бы причинно-следственную связь: отклик появляется на выходе раньше, чем на вход поступило воздействие (см. статью физически реализуемая система).

Применение

Анализ систем

Восстановление частотной характеристики

Важным свойством импульсной характеристики является тот факт, что на её основе может быть получена комплексная частотная характеристика, определяемая как отношение комплексного спектра сигнала на выходе системы к комплексному спектру входного сигнала. Частотная характеристика фильтра определяется какпреобразование Фурье (дискретное преобразование Фурье в случае цифрового сигнала) от импульсной характеристики.

Тел: (495) 223-11-00 с 10 до 20 ч. Подробнее

Переходные и импульсные характеристики электрических цепей

1. Переходные характеристики электрических цепей

Переходная характеристика цепи (как и импульсная) относится к временным характеристикам цепи, т. е. выражает некоторый переходный процесс при заранее установленных воздействиях и начальных условиях.

Для сравнения электрических цепей по их реакции к этим воздействиям, необходимо цепи поставить в одинаковые условия. Наиболее простыми и удобными являются нулевые начальные условия.

Переходной характеристикой цепи называют отношение реакции цепи на ступенчатое воздействие к величине этого воздействия при нулевых начальных условиях.

По определению ,

где – реакция цепи на ступенчатое воздействие;

– величина ступенчатого воздействия [В] или [А].

Так как и делится на величину воздействия (это вещественное число), то фактически – реакция цепи на единичное ступенчатое воздействие.

Если переходная характеристика цепи известна (или может быть вычислена), то из формулы можно найти реакцию этой цепи на ступенчатое воздействие при нулевых НУ

.

Установим связь между операторной передаточной функцией цепи, которая часто известна (или может быть найдена), и переходной характеристикой этой цепи. Для этого используем введенное понятие операторной передаточной функции:

.

Отношение преобразованной по Лапласу реакции цепи к величине воздействия представляет собой операторную переходную характеристику цепи:

Следовательно .

Отсюда находится операторная переходная характеристика цепи по операторной передаточной функции.

Для определения переходной характеристики цепи необходимо применить обратное преобразование Лапласа:

,

воспользовавшись таблицей соответствий или (предварительно) теоремой разложения.

Пример: определить переходную характеристику для реакции напряжение на емкости в последовательной -цепи (рис. 1):

Рис. 1

Здесь реакция на ступенчатое воздействие величиной :

,

откуда переходная характеристика:

.

Переходные характеристики наиболее часто встречающихся цепей найдены и даны в справочной литературе.

2. Интегралы Дюамеля

Переходную характеристику часто используют для нахождения реакции цепи на сложное воздействие. Установим эти соотношения.

Условимся, что воздействие является непрерывной функцией и подводится к цепи в момент времени , а начальные условия – нулевые.

Заданное воздействие можно представить как сумму ступенчатого воздействия приложенного к цепи в момент и бесконечно большого числа бесконечно малых ступенчатых воздействий, непрерывно следующих друг за другом. Одно из таких элементарных воздействий, соответствующих моменту приложения показано на рисунке 2.

Рис. 2

Найдем значение реакции цепи в некоторый момент времени .

Ступенчатое воздействие с перепадом к моменту времени обуславливает реакцию, равную произведению перепада на значение переходной характеристики цепи при , т. е. равную:

.

Бесконечно малое же ступенчатое воздействие с перепадом , обуславливает бесконечно малую реакцию , где есть время, прошедшее от момента приложения воздействия до момента наблюдения. Так как по условию функция непрерывна, то:

.

В соответствии с принципом наложения реакции будет равна сумме реакций, обусловленных совокупностью воздействий, предшествующих моменту наблюдения , т. е.

.

Обычно в последней формуле заменяют просто на , поскольку найденная формула верна при любых значениях времени :

.

Или, после несложных преобразований:

.

Любое из этих соотношений и решает задачу вычисления реакции линейной электрической цепи на заданное непрерывное воздействие по известной переходной характеристики цепи . Эти соотношения называют интегралами Дюамеля.

3. Импульсные характеристики электрических цепей

Импульсной характеристикой цепи называют отношение реакции цепи на импульсное воздействие к площади этого воздействия при нулевых начальных условиях.

По определению ,

где – реакция цепи на импульсное воздействие;

– площадь импульса воздействия.

По известной импульсной характеристике цепи можно найти реакцию цепи на заданное воздействие: .

В качестве функции воздействия часто используется единичное импульсное воздействие называемое также дельта-функцией или функцией Дирака.

Дельта-функция – это функция всюду равная нулю, кроме , а площадь ее равна единице ( ):

К понятию дельта-функция можно прийти, рассматривая предел прямоугольного импульса высотой и длительностью , когда (рис. 3):

Рис. 3

Установим связь между передаточной функцией цепи и ее импульсной характеристикой, для чего используем операторный метод.

По определению:

.

Если воздействие (оригинал) рассматривать для наиболее общего случая в виде произведения площади импульса на дельта-функцию, т. е. в виде , то изображение этого воздействия согласно таблицы соответствий имеет вид:

.

Тогда с другой стороны, отношение преобразованной по Лапласу реакции цепи к величине площади импульса воздействия, представляет собой операторную импульсную характеристику цепи:

.

Следовательно, .

Для нахождения импульсной характеристики цепи необходимо применить обратное преобразование Лапласа:

, т. е. фактически .

Обобщая формулы, получим связь между операторной передаточной функцией цепи и операторными переходной и импульсной характеристиками цепи:

.

Таким образом, зная одну из характеристик цепи, можно определить любые другие.

Произведем тождественное преобразование равенства, прибавив к средней части .

Тогда будем иметь .

Поскольку представляет собой изображение производной переходной характеристики, то исходное равенство можно переписать в виде:

.

Переходя в область оригиналов, получаем формулу, позволяющую определить импульсную характеристику цепи по известной ее переходной характеристике:

.

Если , то .

Обратное соотношение между указанными характеристиками имеет вид: .

По передаточной функции легко установить наличие в составе функции слагаемого .

Если степени числителя и знаменателя одинаковы, то рассматриваемое слагаемое будет присутствовать. Если же функция является правильной дробью, то этого слагаемого не будет.

Пример: определить импульсные характеристики для напряжений и в последовательной -цепи, показанной на рисунке 4.

Рис. 4

Определим :

.

По таблице соответствий перейдем к оригиналу:

.

График этой функции показан на рисунке 5.

Передаточная функция :

.

Согласно таблице соответствий имеем:

График полученной функции показан на рисунке 6.

Рис. 6

Укажем, что такие же выражения можно было получить с помощью соотношений, устанавливающих связь между и .

Импульсная характеристика по физическому смыслу отражает собой процесс свободных колебаний и по этой причине можно утверждать, что в реальных цепях всегда должно выполняться условие:

20. Математические модели систем автоматического управления.

Математические соотношения, которые описывают процессы, протекающие в системах автоматического управления, называют математическими моделями этих систем. Возможность представить систему автоматического управления в виде математической модели является основой для их аналитического исследования.

В основе формирования математической модели систем управления лежит физическое описание всех процессов, которые протекают в исследуемой системе.

Требования к математическим моделям систем автоматического управления:

1.

Математическая модель должна как можно точнее отражать физические процессы в исследуемой системе управления.

2.

Математическая модель системы управления должна быть достаточно простой и наглядной, чтобы излишне не усложнять исследования.

Математическая модель системы управления должна устанавливать связь входной переменной и выходной переменной (см. рисунок).

^

Основные этапы составления математических моделей систем автоматического управления и регулирования:

1.

Разделение системы автоматического управления на отдельные элементы.

Для этой цели составляется функциональная схема системы автоматического управления. На рисунке приведена функциональная схема замкнутой системы управления; система управления с обратной связью.

На функциональной схеме указывают

•

отдельные элементы системы;

•

связь между элементами;

•

направления распространения сигналов и их обозначение;

•

входные и выходные переменные.

2.

Составляются математические модели каждого элемента системы;

3.

Составляются математические модели связей между элементами системы;

4.

Составляются математические модели внутренних и внешних помех, действующих на систему;

5.

Составляются математические модели внешних возмущающих воздействий , действующих на систему.

Совокупность математических моделей элементов системы, моделей связей между этими элементами и математических моделей помех и возмущений действующих на объект управления и на систему управления образуют математическую модель исследуемой системы управления.

Везде далее под системой автоматического управления мы будем понимать ее математическую модель.

Формы представления математических моделей систем автоматического управления:

•

дифференцианые уравнения;

•

передаточные функции;

•

структурные схемы.

21.Передаточная функция

Передаточная функция — один из способов математического описания динамической системы. Используется в основном в теории управления, связи и цифровой обработке сигналов. Представляет собой дифференциальный оператор, выражающий связь между входом и выходом линейной стационарной системы. Зная входной сигнал системы и передаточную функцию, можно восстановить выходной сигнал.

В теории управления передаточная функция непрерывной системы представляет собой отношение преобразования Лапласа выходного сигнала к преобразованию Лапласа входного сигнала при нулевых начальных условиях.

Линейные стационарные системы[править | править исходный текст]

Пусть — входной сигнал линейной стационарной системы, а — её выходной сигнал. Тогда передаточная функция такой системы записывается в виде:

,

где и — преобразования Лапласа для сигналов и соответственно:

,

.

Дискретная передаточная функция

Для дискретных и дискретно-непрерывных систем вводится понятие дискретной передаточной функции. Пусть — входной дискретный сигнал такой системы, а — её дискретный выходной сигнал, . Тогда передаточная функция такой системы записывается в виде:

где и — z-преобразования для сигналов и соответственно:

,

.

Связь с другими динамическими характеристиками

АФЧХ системы можно получить из передаточной функции с помощью формальной замены комплексной переменной на :

.

• Импульсная переходная функция является оригиналом (в смысле преобразования Лапласа) для передаточной функции.

Свойства передаточной функции

1. Для стационарных объектов с сосредоточенными параметрами передаточная функция — это дробно-рациональная функция комплексной переменной ( ):

.

2. Знаменатель и числитель передаточной функции — это характеристические полиномы системы. Полюсы передаточной функции — это корни характеристического полинома в знаменателе, нули — корни характеристического полинома в числителе.

3. В физически реализуемых системах порядок числителя передаточной функции не может превышать порядка её знаменателя .

4. Импульсная переходная функция представляет собой оригинал (преобразования Лапласа) для передаточной функции.

Матричная передаточная функция

Для MIMO-систем вводится понятие матричной передаточной функции. Матричная передаточная функция от вектора входа системы до вектора выхода — это матрица , элемент -й строки -го столбца представляет собой передаточную функцию системы от -й координаты вектора входа системы до -й координаты вектора выхода.

22. Характеристическое уравнение

Характеристическое уравнение

Характеристическое уравнение

Во многих случаях физические процессы, происходящие в системах, описываются системой обыкновенных линейных дифференциальных уравнений с постоянными коэффициентами, которая в достаточно общем случае может быть сведена к дифференциальному уравнению вида

аэродинамические коэффициенты; Z(t) — неизвестная функция времени t; F(t) — заданное, зависящее от времени внешнее возмущение. Если ввести обозначение ">

(при F(t) (≡) 0 это уравнение называется однородным). Здесь а1, b1 — постоянные коэффициенты, выражающиеся, например, через аэродинамические коэффициенты; Z(t) — неизвестная функция времени t; F(t) — заданное, зависящее от времени внешнее возмущение. Если ввести обозначение

di/dti = pi

так, что

diZ(t)/dti = piZ(t),

то это уравнение можно переписать в виде

L(p)Z(t) = S(р)F(t),

где L(р) и S(р) — некоторые многочлены степеней n и m соответственно. Полученный таким образом многочлен

L(р) = рn + a1pn—1 + ... + an—1p + an

называется характеристическим многочленом (полиномом), а уравнение

L(р) = 0

— характеристическим уравнением (существуют и другие способы получения X. у. — см., например, ст. Передаточная функция). Корни X. у. определяют вид решения линейного однородного дифференциального уравнения и тем самым тип собственного движения системы (периодические, затухающее и т. п.). X. у. линейной системы не зависит от того, относительно какой из её переменных (например, скорость полёта или угол атаки при исследовании продольного движения) составляется дифференциальное уравнение и какие возмущающие и задающие воздействия в эту систему вводятся.

Необходимым и достаточным условием устойчивости решения системы обыкновенных линейных дифференциальных уравнений является отрицательность всех действительных частей корней X. у. При этом оказывается, что положительность всех коэффициентов характеристического полинома является необходимым и достаточным условием устойчивости для систем первого и второго порядков и лишь необходимым условием устойчивости (обеспечивается отрицательность только вещественных корней) для систем третьего и более высоких порядков. Существуют различные способы исследования на основе X. у. устойчивости систем, например метод построения областей устойчивости, алгебраические и частотные критерии. X. у. широко используется при исследовании динамики полёта, устойчивости ЛА и его управляемости.

23.Полюса и нули передаточной функции

Передаточная функция ЛНСС имеет вид рациональной функции, т.е. отношения двух полиномов от s. В соответствии с теоремой о разложении многочлена каждый многочлен степени nможет быть единственным образом представлен (факторизован) в виде произведения постоянной и n линейных множителей,

где sk – корни многочлена, корню sk кратности mk соответствует mk множителей (s -sk ).

При этом для многочленов с действительными коэффициентами комплексные корни обязательно встречаются только как комплексно - сопряженные пары. Иначе соответствующие коэффициенты многочлена не будут действительными. Каждая такая пара множителей перемножением может быть представлена как действительный квадратичный множитель .

Таким образом, рациональная передаточная функция системы с действительными коэффициентами может быть представлена в виде (факторизованная форма ПФ):

Здесь - корни многочлена – числителя, они называются нулями H(s),

- корни многочлена – знаменателя называются полюсами H(s), - усиление системы (gain). При этом каждая пара множителей с комплексно-сопряженными корнями можем быть объединена в один квадратичный член.

В точке нуля , в точке полюса .

Пример. Система второго порядка с передаточной функцией . Нули и полюса системы:

График передаточной функции такой системы.

Код: >> [x,y]=meshgrid(-2:0.05:1, -2:0.05:2); s=x+y*j;

>> H=(s+0)./((s+1).^2+1); surf(x,y,abs(H))

Из факторизованного выражения H(s) следует, что нули и полюса однозначно определяют передаточную функцию, а значит и саму систему с точностью до константы k - усиления системы. Следовательно, положение полюсов и нулей ПФ полностью определяет поведение передаточной функции и частотной характеристики системы, т.е. её динамические свойства. Поэтому добавление/удаление полюсов и нулей, выбор их положения широко используются в практике анализа и синтеза систем, чтобы получить систему с нужными свойствами.

В Matlab функция tf2zp(n,d) вычисляет нули, полюса и усиление системы по её системной функции H(s), а функция zp2tf(z,p,k), наоборот, преобразует полюсно – нулевое описание в передаточную функцию системы H(s).

Обычно полюса и нули для наглядности отображаются в виде точек на комплексной плоскости. Например, диаграмма полюсов и нулей для передаточной функции

Вычисление ПФ по расположению нулей и полюсов в Matlab

>> z = -1; p=[-2 1+j 1-j]; k =1; [num,den]=zp2tf(z,p,k)

num = 0 0 1 1

den = 1 0 -2 4 Поэтому

Если , то факторизованная ПФ системы дает её частотную характеристику в виде

Следовательно, АЧХ - произведение/частное членов вида .

Фазо - частотная характеристика равна сумме углов нулей системы минус сумма углов полюсов. Углы отсчитываются от действительной оси плоскости s.

24.Математическая модель САУ в пространстве состояний.

24. Для математического описания САУ по её функциональной схеме (рис. В1) определяется состав её отдельных звеньев, связанных друг с другом и с внешней средой. Основными формами представления операторов преобразования входных переменныхg(t) и f(t) в переменные выхода y(t) в конечномерных линейных непрерывных стационарных детерминированных моделях звеньев и САУ являются линейные дифференциальные уравнения,операторные функции передачи, временные и частотные характеристики [1, 2, 6].

Линейные дифференциальные уравнения описывают процессы, происходящие в каждом звене САУ в виде зависимости выходной величины x2(t) от входного воздействия x1(t). Эти уравнения называются математическими моделями звеньев и для звеньев разной физической природы составляются по законам соответствующей науки (механики, электротехники, термодинамики и др.), нелинейные уравнения линеаризуются. Совокупность уравнений (математических моделей) взаимосвязанных звеньев САУ образуют систему дифференциальных уравнений САУ, называемуюматематической моделью САУ [1, 2, 6].

Для описания математической модели САУ обычно используют три способа [1, 2]:

1) поэлементное описание САУ с учётом взаимодействия каждого звена с другими звеньями и с внешней средой, при этом модель САУ описывается системой дифференциальных уравнений, учитывающих все параметры звеньев, входные и выходные величины (координаты) процессов управления, что обеспечивает возможность физической интерпретации всех процессов управления;

2) системное описание САУ представляется одним уравнением, которое получается из поэлементного описания САУ методом подстановок для исключения промежуточных координат процесса управления и учитывает только зависимость выходного процесса (выходной величины) САУ от входного процесса (входных величин) при утрате возможностей физической интерпретации процессов управления, происходящих внутри САУ;

3) векторно-матричное описание САУ в пространстве переменных состояния системы, позволяющее учитывать все параметры и переменные величины (координаты) САУ и вести расчёты с применением ЭВМ при возможности физической интерпретации происходящих процессов управления в САУ.

Операторная функция передачи (ОФП) (передаточная функция) является важнейшим математическим описанием звена или САУ. ОФП получается из дифференциального уравнения в операторной форме при нулевых начальных условиях (1.1.3) в виде отношения изображений по Лапласу переменных выхода и входа. ОФП широко применяемая в операторно-структурном методе расчета САУ с использованием алгоритмических структурных схем [1, 2, 6]:

(1.1.4)

Временными характеристиками звена или САУ являются переходная функция h(t) и весовая функция w(t) [1, 2, 6].

Переходной функцией (переходной характеристикой) h(t)= =x2(t) звена или САУ называется реакция звена или САУ (переходный процесс выходной величины x2(t)) на единичное ступенчатое входное воздействие x1(t)=1[t] при нулевых начальных условиях.

Весовой функцией (функцией веса, импульсной переходной характеристикой) w(t)=x2(t) звена или САУ называется их реакция на единичное импульсное входное воздействие x1(t)=δ(t) (дельта-функцию или функцию Дирака) при нулевых начальных условиях. Дельта-функция или функция Дирака получается при дифференцировании единичной ступенчатой функции δ(t)==d1[t]/dt, при этом δ(t)=0 в любой момент времени t, кроме t=0, где величина импульса стремится к бесконечности при бесконечно малой продолжительности импульса, а площадь импульса равна единице ∫δ(t)dt=1. Весовая функция w(t) связана с переходной функциейh(t) операцией дифференцирования w(t)=dh(t)/dt.

Частотными характеристиками звена или САУ называются зависимости от частоты ω значений амплитуды А2(ω) и фазового сдвига φ(ω) выходной величины x2(t)=A2(ω) sin(wt+j) в установившихся режимах работы при единичном синусоидальном входном воздействии x1(t)=A1sinwt=1sinωt и изменении частоты ω от 0 до ∞ [1, 2, 6].

Основной частотной характеристикой звена или САУ является амплитудно-фазовая характеристика (АФХ) (частотная передаточная функция, комплексный коэффициент передачи) W(jw), которая получается из передаточной функции (ОФП) W(p) звена или САУ при замене p=jw и изменении частоты ω от 0 до ¥. Например, для звена с ОФП (1.1.4) выражение АФХ запишется

(1.1.5)

где U(w), V(w) — вещественная и мнимая составляющие вектора W(jw); — амплитудная частотная характеристика (АЧХ); j(w)=arctg[V(w)/U(w)] — фазовая частотная характеристика (ФЧХ).

В расчетах САУ часто используются логарифмические частотные характеристики.

Логарифмическая амплитудная частотная характеристика (ЛАЧХ) звена или САУ строится в прямоугольной системе координат, где по оси ординат в линейном масштабе указывается величина ЛАЧХ в децибелах

L(w)=20lg½W(jw)½=20 lg A(w), (1.1.6)

а по оси абсцисс в логарифмическом масштабе указывается частота ω в 1/с (при этом равномерные изменения частоты в 10 раз представляются декадами). Децибел равен 1/10 бела. Бел равен десятичному логарифму отношения мощностей на выходе и входе звена или пропорциональному мощностям отношению квадратов напряжений, токов, скоростей или других физических величин (1бел=lgP2/P1=lgU22/U12). Поэтому в (1.1.6) множитель 20=2

Математическое описание систем управления в нормальной форме пространства состояний

Пусть линейная стационарная одномерная система управления с входным воздействием и выходной координатой описывается моделью в виде дифференциального уравнения n-го порядка с постоянными коэффициентами и в форме «Вход – выход»

или

(1)

Традиционно математическую модель (1) в нормальной форме пространства состояний для систем с записывают так [1, 2]:

;

. (2)

В качестве переменных состояния при представлении математических моделей (1) систем управления в нормальной форме пространства состояний выбираются выходная величина и ее производные.

Коэффициенты при этом вычисляют по формулам

; .

Если степень числителя передаточной функции, соответствующей исходному дифференциальному уравнению, меньше степени знаменателя , коэффициенты полагают равными нулю.

Анализ модели (2) показывает, что входное воздействие в системе при подаётся на вход последнего блока, а выходная координата формируется по первой переменной состояния. Так как каждая переменная состояния вычисляется на основе значений последующей переменной, то при численном интегрировании системы уравнений (2) на первом шаге при в функции входной переменной вычисляется только переменная состояния, на втором шаге переменная и т.д., то есть передача сигнала в системе происходит последовательно от последнего блока к первому, что противоречит естественному прямому порядку вычислений и принципу причинности.

С целью получения математической модели системы в форме пространства состояний с прямой причинно-следственной связью предлагается переменные в (1) вводить, начиная с n-й компоненты вектора состояния [3, 4]. Зададим для системы с переменные состояния v1, v2, ..., vn, связанные с выходной величиной x(t) и ее производными, соотношениями:

(3)

Отличие введённых координат состояния (3) состоит в том, что в качестве й компоненты вектора состояния принята выходная переменная системы, а первой компоненте вектора состояния соответствует производная выходной переменной. С учётом предложенного подхода в матричной форме пространства состояний система уравнений запишется так [5]:

;

. (4)

В модели системы управления в пространстве состояний нормальной формы (4), полученной на основании предложенного подхода, первая компонента непосредственно зависит от входного воздействия, а каждый последующий элемент вектора состояния вычисляется с использованием предыдущей переменной (вторая фазовая координата зависит от первой и т.д.). Выход системы формируется по й компоненте вектора состояния, являющейся в свою очередь функцией й компоненты фазовых координат, а следовательно и всех других координат состояния.

С целью исключения производных от входной величины в дифференциальных уравнениях для систем управления с моделями, содержащими полюсов и нулей, введем новые переменные состояния: , :

(5)

Коэффициенты при производных в правых частях дифференциальных уравнений (5) равны нулю при условиях

Откуда следует рекуррентная формула для вычисления численных значений коэффициентов

(6)

В общем случае для системы управления, передаточные функции которых содержат полюсов и нулей, математическая модель в нормальной форме пространства состояний в соответствии с предложенным подходом и (6) может быть представлена в виде

;

. (7)

Таким образом, предложенный подход к построению математических моделей в пространстве состояний нормальной формы позволяет записать модель системы управления с учётом прямой причинно-следственной связи (7) и избежать погрешностей при моделировании систем на компьютерах. Разработанная математическая модель обеспечивает единство методологических принципов при исследовании, анализе и синтезе систем управления по моделям «Вход – выход» и «Вход – состояние – выход».

Gulzat

25 27 31 jok

26==Структурные схемы. Способы соединения звеньев.

 

Систему автоматического управления можно рассматривать как комбинацию типовых динамических звеньев. Изображение системы управления в виде совокупности типовых и нетиповых динамических звеньев с указанием связей между ними носит название структурной схемы системы. Звено в этом случае выступает как элементарная структурная единица, преобразователь информации.

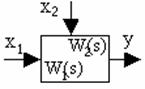
Структурные схемы состоят из отдельных структурных элементов. Основными элементами структурных схем являются следующие.

1. Звено с одним входом и одним выходом: Y(s)=W(s)X(s).

 

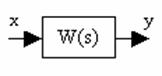
2.   Звено с двумя входами и одним выходом (около каждого входа записывается своя передаточная функция):Y(s)=W1(s)X1(s)+W2(s)X2(s)

3. Линия связи и узел (разветвление), стрелка показывает направление передачи информации.

         и             

4. Сумматор.          

                                 

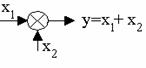
5. Элемент сравнения.

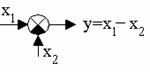 или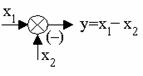     

 

В системах управления встречаются три вида соединений звеньев: последовательное, параллельное и соединение по схеме с обратной связью.

Последовательное соединение звеньев изображено на рис.3.10, такое соединение характеризуется тем, что  выход предыдущего звена подается на вход последующего.

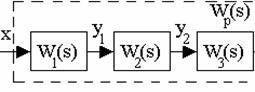
Рис. 3.10. Последовательное соединение звеньев

 

Выходная величина последовательно соединенных звеньев определяется      .

Откуда результирующая передаточная функция   равняется

.

Следовательно, в общем случае можно записать

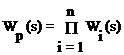,                               (3.51)

где n - число включенных последовательно звеньев.

Таким образом, результирующая передаточная функция последовательно соединенных звеньев равна произведению передаточных функций составляющих звеньев.

Параллельное соединение звеньев изображено на рис.3.11, такое соединение характеризуется тем, что на входы всех звеньев подается одно и то же входное воздействие, а выходная величина определяется суммой выходных величин отдельных звеньев.

 

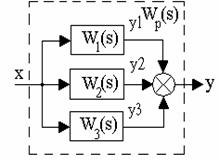
Рис. 3.11. Параллельное соединение звеньев

 

Выходная величина параллельно соединенных звеньев определяется   y=y1+y2+y3, т.е.

.

Тогда              .

В общем случае

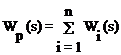,                                 (3.52)

где n - число включенных параллельно звеньев.

Таким образом, результирующая передаточная функция параллельно соединенных звеньев равна сумме передаточных функций составляющих звеньев.

Обратная связь. Такое соединение звеньев изображено на рис.3.12, оно характеризуется тем, что  выходной сигнал звена подается на его вход.

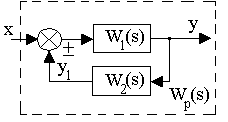
Рис. 3.12. Соединение звеньев по схеме с обратной связью

 

Обратная связь может быть положительной (ПОС), если сигнал y1, снимаемый с выхода второго звена, суммируется с сигналом x на входе, и отрицательной (ООС), если y1  вычитается. Кроме того, обратные связи могут быть жесткими и гибкими. Связь называется гибкой, если передаточная функция W2(s) в установившемся режиме равна нулю.

Для определения результирующей передаточной функции такой комбинации звеньев запишем очевидные соотношения:

  ,         

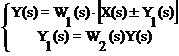где знак “+” относится к положительной, а знак “-” - к отрицательной обратной связи.

Откуда результирующая передаточная функция обратной связи имеет вид

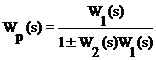  ,                           (3.53)

где знак “+” соответствует ООС, знак “” - ПОС.

В общем случае, сложная цепь динамических звеньев, образующих систему управления, включает в себя комбинации всех трех рассмотренных случаев, т.е. представляет собой смешанное соединение звеньев. Пользуясь выражениями (3.51), (3.52) и (3.53), можно найти общую результирующую передаточную функцию смешанного соединения звеньев.

В тех случаях, когда структурная схема системы оказывается сложной и содержит перекрестные связи, ее упрощают и сводят к простейшему эквивалентному виду, пользуясь правилами преобразования структурных схем [1,2,7].

 27 jok

28 При́нцип суперпози́ции — один из общих законов во многих разделах физики. В самой простой формулировке принцип суперпозиции гласит:

• результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил

Наиболее известен принцип суперпозиции в электростатике, в которой он утверждает, что напряженность электростатического поля, создаваемого в данной точке системой зарядов, есть сумма напряженностей полей отдельных зарядов.

Принцип суперпозиции может принимать и иные формулировки, которые полностью эквивалентны приведённой выше:

• Взаимодействие между двумя частицами не изменяется при внесении третьей частицы, также взаимодействующей с первыми двумя.

• Энергия взаимодействия всех частиц в многочастичной системе есть просто сумма энергий парных взаимодействий между всеми возможными парами частиц. В системе нет многочастичных взаимодействий.

• Уравнения, описывающие поведение многочастичной системы, являются линейными по количеству частиц.

Именно линейность фундаментальной теории в рассматриваемой области физики есть причина возникновения в ней принципа суперпозиции.

Принцип суперпозиции в электродинамике

Принцип суперпозиции является следствием, прямо вытекающим из рассматриваемой теории, а вовсе не постулатом, вносимым в теорию a priori. Так, например, вэлектростатике принцип суперпозиции есть следствие того факта, что уравнения Максвелла в вакууме линейны. Именно из этого следует, что потенциальную энергию электростатического взаимодействия системы зарядов можно легко сосчитать, вычислив потенциальную энергию каждой пары зарядов.

Другим следствием линейности уравнений Максвелла является тот факт, что лучи света не рассеиваются и вообще никак не взаимодействуют друг с другом. Этот закон можно условно назвать принципом суперпозиции в оптике.

Подчеркнём, что электродинамический принцип суперпозиции не есть незыблемый закон Природы, а является всего лишь следствием линейности уравнений Максвелла, то есть уравнений классической электродинамики. Поэтому, когда мы выходим за пределы применимости классической электродинамики, вполне стоит ожидать нарушения принципа суперпозиции.

Примеры нарушения электродинамического принципа суперпозиции

Если рассматривается электродинамика не в вакууме, а в какой-либо среде, то принцип суперпозиции может нарушаться. Так, например, если поляризуемость илинамагниченность среды нелинейно зависят от приложенного поля, это приводит к нелинейным поправкам в уравнениях Максвелла. Прямым следствием этого является нарушение принципа суперпозиции в такой нелинейной среде.

В некоторых случаях эти нелинейности невелики, и принцип суперпозиции с некоторой степенью приближения может выполняться. В других случаях нарушение принципа суперпозиции велико и может приводить к принципиально новым явлениям. Так, например, два луча света, распространяющиеся в нелинейной среде, могут изменять траекторию друг друга. Более того, даже один луч света в нелинейной среде может воздействовать сам на себя и изменять свои характеристики. Многочисленные эффекты такого типа изучает нелинейная оптика.

Принцип суперпозиции нарушается также в вакууме при учёте квантовых явлений. В квантовой электродинамике фотон может на некоторое время превратиться вэлектрон-позитронную пару, которая уже может взаимодействовать с другими фотонами. Эффективно это приводит к тому, что фотоны могут взаимодействовать друг с другом. Такого типа процессы (рассеяние света на свете и другие процессы нелинейной электродинамики) наблюдались экспериментально.

29==Частотные характеристики САУ

Частотные характеристики системы характеризуют реакцию элементарного звена, объекта управления или всей системы на гармоническое воздействие в установившемся режиме.

Пусть на вход звена подано гармоническое воздействие:

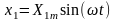(6.6) где 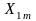- амплитуда;

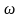- угловая частота этого воздействия.

Выходной сигнал линейного звена в установившемся режиме будет также представлять собой гармоническую функцию:

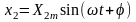(6.7) где 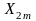- амплитуда;

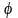- угол сдвига выходного гармонического сигнала по отношению к входному (сдвиг по фазе).

С учетом введенных обозначений модуль частотной передаточной функции представляет собой отношение амплитуды выходной сигнала к амплитуде входного в установившемся режиме, т. е.

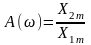, (6.8)

а аргумент частотной передаточной функции - сдвиг фазы выходной величины по отношению к входной величине на данной частоте.

Таким образом, амплитудная частотная характеристика (АЧХ) 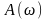отражает изменение амплитуды выходного сигнала звена при пропускании звеном входного сигнала различной частоты. Фазовая частотная характеристика (ФЧХ) 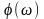показывает фазовые сдвиги, вносимые звеном на различных частотах входного сигнала.

Амплитудно-фазовая частотная характеристика (АФЧХ) строится в полярных координатах на комплексной плоскости . Она представляет собой геометрическое место концов вектора (годограф), соответствующих частотной передаточной функции 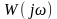при изменении частоты от нуля до бесконечности.

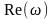Н а рис. 6.1 в качестве примера приведена АФЧХ динамического звена (фильтра) третьего порядка. По оси абсцисс АФЧХ откладывается вещественная часть , а по оси ординат - мнимая часть 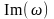. Годограф описывает изменение амплитуды и фазы выходного сигнала при изменении частоты входного сигнала. Заметим, что при изменении частоты от нуля до бесконечности амплитуда годографа уменьшается от некоторого ненулевого значения до нуля, а фаза выходного сигнала стремится к величине -270˚ (вращение годографа против часовой стрелке принято положительным). Заметим также, что изменение частоты от нуля до минус бесконечности соответствует зеркальному отображению АФЧХ на комплексной плоскости относительно оси абсцисс.

Рис. 6.1. Амплитудно-фазовая частотная характеристика динамического

звена третьего порядка

Диапазон изменения частоты входного сигнала теоретически равен бесконечности. Поэтому часто при анализе и синтезе систем автоматического управления используются логарифмические частотные характеристики (диаграмму Боде) - логарифмические амплитудные частотные характеристики (ЛАЧХ) и логарифмические фазовые частотные характеристики (ЛФЧХ), когда по оси абсцисс круговая частота 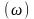откладывается в логарифмическом масштабе. При этом ЛАЧХ определяют выражением

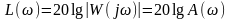. (6.9)

В табл. 6.1 приведены соотношения, связывающие модуль частотной передаточной функции и ее логарифмический эквивалент 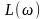, выражаемый в децибелах.

Таблица 6.1

	0,001	0,01	0,1	1	10	100	1000
	-60	-40	-20	0	20	40	60

В качестве примера рассмотрим простейшее инерционное звено (апериодический фильтра 1-го порядка), описываемое передаточной функцией

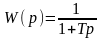, (6.10) где T – постоянная времени фильтра.

Частотная передаточная функция этого звена

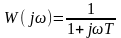. (6.11)

Домножая числитель и знаменатель (6.11) на комплексно сопряженное знаменателю выражение и выделяя действительную и мнимую части, получим

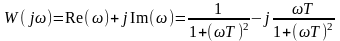(6.12) или в показательной форме

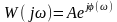, (6.13) где 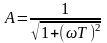- модуль частотной характеристики,

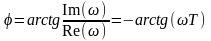- аргумент частотной характеристики.

Выражение для ЛАЧХ апериодического фильтра

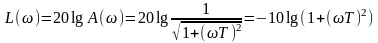. (6.14)

АФЧХ апериодического фильтра можно получить, используя выражения (6.12) или (6.13) при изменении частоты от нуля до бесконечности. Она имеет вид полуокружности с центром в точке (1/2, 0) комплексной плоскости (рис. 6.2).

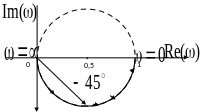
Рис. 6.2. АФЧХ

апериодического звена

30==Частотные передаточные функции

Частотная передаточная функция является важнейшей характеристикой динамической системы управления. В теории автоматического управления она используется, когда необходимо получить частотные характеристики системы по ее передаточной функции.

Для однозначного преобразования некоторой непрерывной функции времени 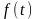в функцию частоты служит прямое преобразование (изображение) Фурье [1, 2]

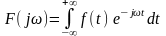. (6.1)

Частотной передаточной функцией системы называется отношение изображения Фурье ее выходной переменной к изображению Фурье входной переменной.

Если непрерывная функция времени равна нулю при t < 0, то частотная передаточная функция системы легко может быть найдена по ее передаточной функции при подстановке 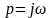, где p – символ преобразования Лапласа, т. е.

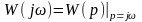(6.2)

Функция может быть представлена в показательной форме или в форме координат вектора на комплексной плоскости в следующем виде:

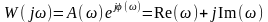(6.3) где - модуль частотной передаточной функции,

- аргумент или фаза частотной передаточной функции;

- соответственно вещественная и мнимая составляющие частотной передаточной функции.

Из теории комплексных чисел [1, 2] известны следующие выражения, позволяющие сделать переход из показательной формы комплексного числа в алгебраическую форму:

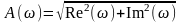, (6.4)

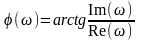. (6.5)

Изменение модуля и аргумента частотной передаточной функции при изменении частоты входного сигнала дает полезную информацию, необходимую для анализа и синтеза систем управления в частотной области.

Для анализа частотных свойств звеньев и синтеза корректирующих звеньев САУ используются так называемые частотные характеристики: амплитудная частотная характеристика (АЧХ), фазовая частотная характеристика (ФЧХ) и амплитудно-фазовая частотная характеристика (АФЧХ).

32==Амплитудно-частотная характеристика (АЧХ) — зависимость амплитуды выходного сигнала от частоты. А также функция выражающая (описывающая) эту зависимость. А также — график этой функции. (Математически амплитуда — это модуль некоторой комплекснозначной функции от частоты.) Также может рассматриваться АЧХ других комплекснозначных функций частоты, например, спектральной плотности мощности сигнала.

АЧХ в теории автоматического управления

АЧХ в теории линейных стационарных систем означает зависимость модуля передаточной функции системы от частоты. АЧХ показывает во сколько раз амплитуда сигнала на выходе системы отличается от амплитуды входного сигнала на всём диапазоне частот.

На графике АЧХ по оси абсцисс откладывается частота, а по оси ординат отношение амплитуд выходного и входного сигналов системы. Обычно для частоты используется логарифмический масштаб, так как исследуемый диапазон частот может изменяться в достаточно широких пределах (от единиц до миллионов Гц или рад/с). В случае когда логарифмический масштаб используется и на оси ординат, АЧХ превращается в логарифмическую амплитудно-частотную характеристику. ЛАЧХ получила широкое распространение в теории автоматического управления в связи с простотой построения и наглядностью при исследовании систем управления.

Фа́зо-часто́тная характеристика (ФЧХ) — зависимость разности фаз между выходным и входным сигналами от частоты сигнала, функция, выражающая (описывающая) эту зависимость, также — график этой функции.

• Для линейной электрической цепи, зависимость сдвига по фазе между гармоническими колебаниями на выходе и входе этой цепи от частоты гармонических колебаний на входе.

Часто ФЧХ используют для оценки фазовых искажений формы сложного сигнала, вызываемых неодинаковой задержкой во времени его отдельных гармонических составляющих при их прохождении по цепи.

Определение ФЧХ

• В теории управления ФЧХ звена определяется из равенства её тангенса отношению мнимой части АФЧХ к действительной:

Enlik

36 jok

34.