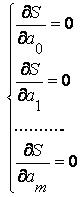35.Методы обработки и анализа экспериментальных данных. Сущность метода наименьших квадратов.

Метод наименьших квадратов (МНК, англ. Ordinary Least Squares, OLS) — математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов некоторых функций от искомых переменных. Он может использоваться для «решения» переопределенных систем уравнений (когда количество уравнений превышает количество неизвестных), для поиска решения в случае обычных (не переопределенных) нелинейных систем уравнений, для аппроксимации точечных значений некоторой функцией. МНК является одним из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным. Пусть дана система уравнений , где  — некоторые функции,  — некоторые известные значения, x — набор неизвестных (искомых) переменных. Для произвольных значений значения отличаются от . Суть метода наименьших квадратов заключается в том, чтобы найти такие значения , при которых минимизируется сумма квадратов отклонений (ошибок)  :

В случае, если система уравнений имеет решение, то минимум суммы квадратов будет равен нулю и могут быть найдены точные решения системы уравнений аналитически или, например, различными численными методами оптимизации. Если система переопределена, то есть количество независимых уравнений больше количества искомых переменных, то система не имеет точного решения и метод наименьших квадратов позволяет найти некоторый «оптимальный» вектор . Оптимальность здесь означает максимальную близость векторов и или максимальную близость вектора отклонений к нулю (близость понимается в смысле евклидова расстояния).

В частности, метод наименьших квадратов может использоваться для «решения» системы линейных уравнений

,

где матрица не квадратная, а прямоугольная размера (точнее ранг матрицы A больше количества искомых переменных).

Такая система уравнений, в общем случае не имеет решения. Поэтому эту систему можно «решить» только в смысле выбора такого вектора , чтобы минимизировать «расстояние» между векторами и . Для этого можно применить критерий минимизации суммы квадратов разностей левой и правой частей уравнений системы, то есть . Нетрудно показать, что решение этой задачи минимизации приводит к решению следующей системы уравнений

36.Метод наименьших квадратов. Виды приближающих функций. Метод наименьших квадратов

При интерполировании основным условием является совпадение значений функции и значений интерполяционного многочлена в узлах интерполяции.

Однако при большом количестве узлов интерполяции получается высокая степень многочлена, что затрудняет вычисление. Кроме того, экспериментальные данные, полученные в результате измерений или наблюдений, могут содержать ошибки, которые вызваны несовершенством измерительных приборов, различными случайными факторами. Построение аппроксимирующего многочлена с условием обязательного прохождения его графика через эти экспериментальные точки будет означать повторение ошибок. Поэтому иногда целесообразней строить многочлен, график которого проходит «близко» от заданных точек.

Итак, пусть при изучении неизвестной функциональной зависимости y от x получена таблица значений:

 

x0	x1	…	xn
y0	y1	…	yn

 

Нужно найти эмпирическую зависимость y=f(x), значение которых при x=x_i мало отличались бы от опытных данных y_i. График функции y=f(x), вообще говоря, не проходит через точки (x_i, y_i), как в случае интерполяции, что приводит к сглаживанию экспериментальных данных (рис. 3.3)

 

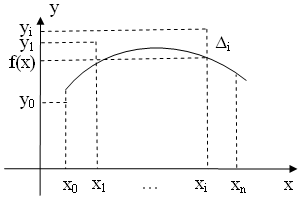
Рис. 3.3

 

Построение эмпирической формы состоит из двух этапов:

1)      выбор общего вида зависимости;

2)      выбор наилучших значений параметров, входящих в формулу.

Метод наименьших квадратов не дает возможности выбрать вид зависимости, он позволяет лишь оптимально подобрать параметры приближающей функции. Вид зависимости выбирается из каких-либо дополнительных соображений: физических, геометрических т.д.

Будем считать, что тип эмпирической зависимости выбран, и ее можно записать в виде:

где f – известная функция; - неизвестные постоянные параметры, значения которых надо найти.

В каждой точке x_i вычислим разность между табличным значением функции y_i и вычисленным значением:

Δ_i - назовем отклонениями. Поскольку y_i и f(x_i , a₀ , … , a_m), вообще говоря, не совпадают все или некоторые Δ_i ≠ 0. Запишем сумму квадратов отклонений для всех точек

.

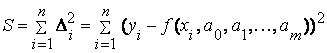1)      S является функцией от независимых переменных a₀ , a₁ , … , a_m

2)      Параметры a₀ , a₁ , … , a_m будем находить из условия минимума функции S.

1)      Минимум найдем, приравнивая к нулю частные производные по этим переменным

(3.5)

 

Из системы уравнений (3.5) найдем a₀ , a₁ , … , a_m.

Геометрически (рис. 3.4) метод наименьших квадратов можно интерпретировать так: среди бесконечного множества линий данного вида, проведенных относительно данных экспериментальных точек, выбрать одну, для которой сумма квадратов отклонений будет наименьшей. Это приводит к сглаживанию экспериментальных данных (рис. 3.3).

 

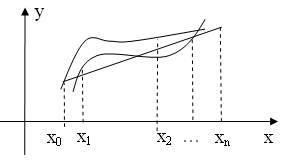
Azamat

37)

Приведенный в предыдущем параграфе классический метод (метод множителей Лагранжа) можно использовать тогда, когда целевая функция и ограничения задачи НЛП обладают хорошими свойствами (гладкость, выпуклость и др.). В отсутствии такой возможности применяются приближенные методы. Они могут применятся и в тех случаях, когда задача (1)-(3) не имеет оптимального решения. Тогда решая обобщенную задачу НЛП приближенными методами, можно построить минимизирующую последовательность, сходящуюся к некоторому, практический приемлемому приближенному «оптимальному решению». Приближенные методы, как правило, являются прямыми методами, так как они решают непосредственно исходную экстремальную задачу. К непрямым методам относятся те, в которых решение исходной задачи получается путем решения другой задачи, к которой предварительно сводится исходная задача. Например, метод множителей Лагранжа является непрямым методом, так как решается задача, полученная из исходной с помощью необходимого условия минимума. В теории НЛП разработано большое число вычислительных методов, которые по тем или иным характеристикам могут быть разбиты на различные группы (классы). Ниже приводится краткие сведения о некоторых из них. Но часто такое разбиение носит условный характер, так как один и тот же метод может быть отнесен к разным группам. Например, методы проекции градиента и условного градиента могут считаться как градиентными методами, так и методами возможных направлений.

1) Алгоритм — это понятное и точное предписание исполнителю совершить последовательность действий, направленных на решение поставленной задачи или достижение указанной цели. Понятие исполнителя алгоритма можно определить с помощью какой-либо формализации. Исполнителем может быть человек, группа людей, робот, станок, компьютер и т.д. Важнейшим свойством, характеризующим любого из этих исполнителей, является то, что исполнитель умеет выполнять некоторые команды. Так, исполнитель – человек умеет выполнять различные команды, такие как «встать», «сесть», «лечь спать» и т.д. Вся совокупность команд, которые данный исполнитель умеет исполнять, называется системой команд исполнителя. Алгоритм, составленный для некоторого исполнителя, можно представить различными способами: графического и словесного описания, в виде таблицы, последовательностью формул, записанным на алгоритмическом языке (язык программирования).

2) Элементарные конструкции языка ПАСКАЛЬ включают в себя имена, чис- ла и строки.Имена (идентификаторы) называют элементы языка - константы, метки, типы, переменные, процедуры, функции, модули, объекты. Имя - это пос- ледовательность букв и цифр, начинающаяся с буквы. В именах может ис- пользоваться символ _ подчеркивание. Имя может содержать произвольное количество символов, но значащими являются 63 символа.Не разрешается в языке ПАСКАЛЬ использовать в качестве имен слу- жебные слова и стандартные имена, которыми названы стандартные конс- танты, типы, процедуры, функции и файлы.Для улучшения наглядности программы в нее могут вставляться пробе- лы. По крайней мере один пробел требуется вставить между двумя последовательными именами, числами или служебными и стандартными име- нами. Пробелы нельзя использовать внутри имен и чисел. Структурированные типы языка программирования высокого уровня. Массивы. Примеры задач с численными, символьными, булевскими массивами. Строковый тип данных. Записи. Оператор присоединения. Записи с вариантами. Множественный тип. Задание множественного типа и множественной переменной. Операции над множествами. Операции отношения. Примеры задач на множественный тип. Файлы. Понятие логического и физического файлов. Файловые типы. Общие процедуры для работы с файлами. Типизированные файлы. Текстовые файлы. Нетипизированные файлы и процедуры ввода-вывода. Прямой и последовательный доступ к компонентам файлов. Turbo Pascal (произносится «ту́рбо паска́ль») — интегрированная среда разработки программного обеспечения для платформ DOS и Windows 3.x и язык программирования в этой среде, диалект языка Паскаль от фирмы Borland.Товарный знак Borland Pascal был зарезервирован для дорогих вариантов поставки (с бо́льшим количеством библиотек и исходным кодом стандартной библиотеки), оригинальная дешёвая и широко известная версия продавалась как Turbo Pascal. Название Borland Pascal также используется в более широком смысле — как неофициальное название версии языка Паскаль от фирмы Borland

3) Оператор — это элемент языка, задающий полное описание действия, которое необходимо выполнить. Каждый оператор представляет собой законченную фразу языка программирования и определяет некоторый вполне законченный этап обработки данных. В состав операторов могут входить служебные слова, данные, выражения и другие операторы. В английском языке данное понятие обозначается словом “statement”, означающим также “предложение” Все операторы языка Паскаль можно разбить на две группы: простые и структурированные. Оператор присваивания

С помощью этого оператора переменной или функции присваивается значение выражения.Для этого используется знак присваивания := , слева от которого записывается имя переменной или функции, которой присваивается значение, а справа - выражение, значение которого вычисляется перед присваиванием.

4) Арифметическим называется выражение, составленное из операндов – величин, над которыми производится операция, скобок и знаков операций. В результате вычисления выражения получается значение определенного типа. В логическом операторе присваивания слева от знака присваивания указывается переменная логического типа (boolean), а справа дается логическое выражение, имеющее значение True (правда) или False (ложь)Символьный знак равенства позволяет Mathcad выйти за рамки численного вычисления выражений. Можно подумать, что это обычный знак =. В отличие от обычного знака равенства, который всегда возвращает число, символьный знак равенства может возвращать выражение.Чтобы иметь возможность использовать символьный знак равенства, требуется Mathcad PLUS. Перечисляемый тип данных - это упорядоченная последовательность скалярных констант, которые составляют этот тип. В качестве значения каждой из констант мы используем ее имя. Имена разных констант разделяются запятыми, а совокупность констант, имеющих перечисляемый тип, помещается в круглые скобки Интервальный тип данных.Диапазон значений, имеющих любой порядковый тип, определяется как интервальный тип данных. Отрезок устанавливается в диапазоне от минимального значения констант до максимального, которые отделяются друг от друга двоеточием "..". Константами могут выступать константы целого, символьного, логического или перечисляемого типа. Базовым типом называют скалярный тип, на котором задается отрезок. упорядоченные и неупорядоченные списки работают одинаково, за исключением того, что последние используются для представления непоследовательных списков, элементы которых обычно маркируются крупной черной точкой (буллитом), а первые используются для представления последовательных списков, которые обычно имеют вид элементов пронумерованных в возрастающем порядке.Для определения неупорядоченных списков используется тег ul, а для определения упорядоченных списков – тег ol. Внутри списков для определения каждого отдельного элемента списка используется тег

5) Следовательно, любой язык программирования должен иметь инструменты как для ввода данных, так и их вывода. В Паскале ввод осуществляется с помощью процедур read() и readln(), а вывод - благодаряwrite() и writeln(). Процедуры, которые имеют окончание ln, после своего выполнения переводят указатель на новую строку.Откуда или с помощью чего можно ввести данные в программу? Обычно это можно сделать с помощью клавиатуры или из файлов. Программа должна правильно выполняться при любых значениях начальных данных. Должна быть проверена правильность работы всех ветвей программы на тестах. При отсутствии решения должно выводиться сообщение "Нет решения" и значения соответствующих исходных и промежуточных данных.Для организации разветвлений в программах используются операторы безусловного и условного переходов и оператор выбора.Оператор безусловного перехода записывается в виде GOTO n, где n-метка оператора, на который происходит переход, Условный оператор реализует выполнение определённых команд при условии, что некоторое логическое выражение (условие) принимает значение «истина» true. В большинстве языков программирования условный оператор начинается с ключевого словаif. Оператор ветвления (условная инструкция, условный оператор) — оператор, конструкция языка программирования, обеспечивающая выполнение определённой команды (набора команд) только при условии истинности некоторого логического выражения, либо выполнение одной из нескольких команд (наборов команд) в зависимости от значения некоторого выражения. Для реализации ветвления алгоритмов и проверки условий  в языке Visual Basic используется условный оператор IF. Необходимо отметить следующее: после выполнения блока действий оператор будет считаться выполненным и программа перейдет к следующему оператору. Это означает, что если переменная будет соответствовать двум и более условиям, указанным после ключевого слова Case, то будет выполнен только блок действий первого условия

Tileujankizi