1. Анализ существующих методов решения задачи

Прямые методы решения СЛАУ. К прямым (или точным) методам решения СЛАУ относятся алгоритмы, которые в предположении, что вычисления ведутся без округлений, позволяют получить точное решение системы за конечное число арифметических действий. Чаще всего решение задач такими методами осуществляется поэтапно: на ᴨȇрвом этаᴨȇ систему преобразуют к тому или иному простому виду, на втором - решают упрощенную систему и получают значения неизвестных.

Запишем систему линейных алгебраических уравнений в развернутом виде:

где x₁, x₂,..., x_n - неизвестные величины, b₁, b₂,..., b_n - элементы правой части. Если определитель системы отличен от нуля, то она имеет единственное решение. Для удобства дальнейших преобразований обозначим элементы правой части а_i(n+1) и запишем расширенную матрицу размерами n(n+1), которая содержит всю информацию о системе:

A =.

С этой матрицей можно обращаться так же, как и с системой - ᴨȇреставлять строки, прибавлять кратное одной строки к другой, исключая неизвестные и приводя матрицу к треугольному или диагональному виду.

Приведем формальное описание схем некотоҏыҳ прямых методов.

Метод Гаусса (схема единственного деления). Алгоритм метода состоит из двух этапов. Первый этап называется прямым ходом метода и заключается в последовательном исключении неизвестных из уравнений, т.е. в приведении матрицы А к верхнему треугольному виду (ниже главной диагонали все нули). Для этого на ᴨȇрвом шаге разделим ᴨȇрвое уравнение системы на а₁₁ (предположим, что коэффициент а₁₁ 0, в противном случае осуществляем ᴨȇрестановку уравнений системы). Обозначим коэффициенты полученного приведенного уравнения , домножим его на коэффициент а₂₁ и вычтем из второго уравнения системы, исключая тем самым х₁ из второго уравнения (обнуляя коэффициент а₁₂ матрицы). Поступим аналогично с остальными уравнениями и получим новую систему, матрица которой в ᴨȇрвом столбце, кроме ᴨȇрвого элемента, содержит только нули, т.е.

.

Первое уравнение в дальнейших преобразования не участвует. Описанный выше процесс исключения неизвестных применим к матрице размерами (n-1) n.После k аналогичных шагов получим k приведенных уравнений с коэффициентами

и матрицу размерами (n - k) (n - k+1), элементы которой вычисляются по формулам

.

Элементы , на которые осуществляется деление, называются ведущими элементами метода Гаусса и не должны равняться нулю. Прямой ход метода Гаусса заканчивается после n шагов определением .

Обратный ход метода Гаусса заключается в последовательном определении компонент решения, начиная с х_n и заканчивая х₁, по следующим формулам:

Метод Гаусса с выбором главного элемента. Метод заключается в том, что при прямом ходе в алгоритме метода Гаусса на каждом шаге исключения производится выбор наибольшего по модулю элемента в качестве ведущего. Этого достигают ᴨȇрестановкой строк или столбцов матрицы коэффициентов. Наиболее распространённой в вычислительной практике является стратегия выбора главного элемента столбца - нахождение максимального по модулю элемента k-го столбца матрицы и использование его в качестве ведущего элемента на k-м шаге исключения. В этом случае для невырожденных систем гарантируется, что ведущие элементы не равны нулю, и уменьшается погрешность при делении и последующем вычитании при преобразованиях. Рекомендуется также масштабировать предварительно каждое уравнение исходной системы, разделив на его самый значительный по абсолютной величине коэффициент. Это делает рост элементов промежуточных матриц ограниченным.

Метод оптимального исключения. В целях экономии оᴨȇративной памяти (примерно в 4 раза) оᴨȇрации прямого и обратного хода метода Гаусса выполняются поᴨȇременно. На ᴨȇрвом шаге после приведения ᴨȇрвого уравнения исключается неизвестное x₁ из второго уравнения, а затем с помощью приведенного второго уравнения - неизвестное x₂ из ᴨȇрвого. После (k-1) таких шагов матрица системы имеет вид

.

На k-м шаге, используя ᴨȇрвые k уравнений, исключаем неизвестные x₁,..,x_k из (k+1)-го уравнения. Затем посредством этого уравнения исключается неизвестное x_k+1 из ᴨȇрвых k уравнений и т.д. В результате прямого хода матрица системы приводится к диагональному виду с единицами на главной диагонали. При этом отпадает необходимость обратного хода, поскольку столбец правой части приведенной матрицы и является вектором решения.

Метод Гаусса-Жордана. Эта модификация метода Гаусса незначительно отличается от метода оптимального исключения. Оᴨȇрации исключения ᴨȇременных для каждого приводимого уравнения осуществляют не только ниже, но и выше главной диагонали. Оᴨȇрации с ᴨȇрвым уравнением системы полностью аналогичны стандартной схеме. Второе уравнение системы после приведения и домножения на соответствующие коэффициенты вычитаем не только из третьего и последующих уравнений, но и из ᴨȇрвого. В результате k таких шагов получаем матрицу

.

Как и в методе оптимального исключения, матрица системы приводится к диагональному виду и вектором решения является столбец .

LU - разложение. Матрицу A можно представить в виде произведения нижней треугольной матрицы (включая диагональ) L (lower) и верхней треугольной матрицы U ( upper ), т.е. A=LU. Это равенство равносильно n² числовым равенствам

.

Разложение матрицы A на множители обычно получают посредством алгоритма, который называется компактной схемой метода Гаусса. Элементы l_im иU_mi могут быть вычислены по формулам

Тогда решение системы Ax=b сводится к последовательному решению двух систем - Ly=b и Ux=y.

Рассмотренный метод можно применять к решению серии систем с одной и той же матрицей.

Метод простых итераций (Якоби).

Для решения итерационным методом система линейных алгебраических уравнений Ax = b должна быть приведена к виду x = Gx+f , где G - некоторая матрица, f - преобразованный вектор свободных членов. Затем выбирается начальное приближение - произвольный вектор x⁽⁰⁾ - и строится рекуррентная последовательность векторов x⁽¹⁾, x⁽²⁾,..., x^(k),... по формуле

.

Для сходимости этой последовательности при любом начальном приближении необходимо и достаточно, чтобы все собственные значения матрицы Gбыли по абсолютной величине меньше единицы. На практике это трудно проверить, и обычно пользуются достаточными условиями сходимости - итерации сходятся, если какая-нибудь норма матрицы меньше единицы, т.е.

или .

Чем меньше норма матрицы G, тем быстрее сходится итерационный процесс.

Преобразование системы можно осуществить, просто решая каждое i-е уравнение относительно x_i :

.

Метод Якоби использует следующий алгоритм построения приближений:

.

Если A - матрица с доминирующей диагональю, т.е. , то метод Якоби сходится при любом начальном приближении x⁽⁰⁾.

Метод Якоби относится к одношаговым итерационным методам, когда для нахождения x^(k+1) требуется помнить только одну предыдущую итерацию x^(k). Для исследования сходимости удобнее записывать итерационные методы не в координатной, а в матричной форме, придерживаясь стандартной формы записи итерационных методов.

Канонической формой одношагового итерационного метода решения СЛАУ называется его запись в виде

где B_k+1 - матрица, задающая тот или иной итерационный метод, _k+1 - итерационный параметр. Числовые параметры _k вводят для ускорения сходимости. Способ выбора итерационных параметров определяется при исследовании сходимости метода, когда выясняется при каких значениях параметров метод сходится и когда сходимость будет наиболее быстрой (соответствующие параметры называются оптимальными).

Итерационный метод называют явным, если B_k+1 - единичная матрица. Неявные итерационные методы имеет смысл применять лишь в том случае, когда решение системы уравнений с матрицей B_k требует меньше машинной памяти или времени или алгоритмически проще, чем решение исходной системы.

Методом простой итерации называют явный метод с постоянм параметром или,

где r^(k) = Ax^(k)-b - вектор невязки. Метод сходится для симметричных положительно определенных матриц при .

Для окончания итерационного процесса используют три способа. При ᴨȇрвом определяют величину стабилизации и прекращают вычисления, если она меньше , т.е.

Недостатком этого способа является то, что при медленно сходящихся итерациях величина стабилизации может быть малой, хотя приближенное решение сильно отличается от точного.

При втором способе вычисляют нормы невязки до начала итераций и на каждой итерации. Итерации прекращают при выполнении неравенства.

При третьем способе предварительно оценивается число итераций, необходимое для получения заданной точности . Если для погрешности итерационного метода выполняются оценки

где q (0,1), то метод сходится со скоростью геометрической прогрессии со знаменателем q. Можно определить, потребовав, чтобы qⁿ < , число итераций n, достаточное для того, чтобы начальная погрешность уменьшилась в заданное число раз:

Целая часть числа n₀() является минимальным числом итераций, необходимым для получения заданной точности .

Величина ln(1/q) является скоростью сходимости итерационного метода.

14. Численные методы решения систем линейных алгебраических уравнений. Метод Зейделя.

ЗЕЙДЕЛЯ МЕТОД

- итерационный метод решения системы линейных алгебраич. уравнений Ах=b. Решение системы х* находится как пределпоследовательности   вычисляемой по правилу

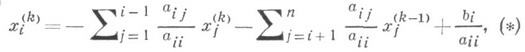
i=l, 2, ..., п,

где a_ij- элементы матрицы А, b_i - компоненты вектора b;диагональные элементы матрицы Апредполагаются отличными от нуля. Вычисления (*) отличаются от простой итерации метода лишь тем, что на k-м шаге при вычислении i-й компоненты учитываются вычисленные k-в приближения первых (i-1) компонент.

В матричной записи 3. м. представляется следующим образом. Если А=В+С, где

то соотношение (*) соответствует матричному соотношению x^(k)=- В ^-1 Сх^(k-1)+В ^-1b. З. м. равносилен методу простой итерации, примененному к системе x=-B^-1Cx+B^-1b, эквивалентной исходной. Для сходимости 3. м. необходимо и достаточно, чтобы все собственные значения матрицы В ^-1 С по модулю были меньше 1. Иначе, чтобы все корни уравнения det(C+Вl)=0 были по модулю меньше 1.

На практике более удобны следующие достаточные условия сходимости 3. м. 1) Пусть при всех i,

 д<1. Тогда 3. м. сходится и для

скорости сходимости имеет место оценка:

2) Пусть А- эрмитова положительно определенная матрица. Тогда 3. м. сходится.

З. м. относится к классу релаксации методов, наиболее употребительным из к-рых является сверхрелаксации метод.

Известны модификации 3. м., использующие предварительное преобразование исходной системы в эквивалентную ей системуx=Mx+f (см. [4]).

15.Элементы линейного программирования.

Определение 1. Линейное программирование – наука о методах исследования и отыскания экстремальных значений линейной функции, на неизвестные которой наложены линейные ограничения. Эта линейная функция называется целевой, а ограничения, которые математически записываются в виде уравнений или неравенств, называются системой ограниченийОпределение 2. Математическое выражение целевой функции и системы ограничений называется математической моделью экономической задачи.Определение 3. Допустимым решением задачи линейного программирования называется вектор  , удовлетворяющий системе ограничений.Определение 4. Допустимое решение, при котором целевая функция достигает своего экстремального значения, называется оптимальным решением задачи линейного программирования и обозначается  . Определение 5. Если все ограничения системы заданы уравнениями и переменные   неотрицательные, то такая модель задачи называется канонической. Если хотя бы одно ограничение является неравенством, то модель задачи ЛП является неканонической.

16.Подход к решению задач линейного программирования

1Графический метод решения задачи линейного программирования основан на геометрической интерпретации задачи линейного программирования и применяется в основном при решении задач двумерного пространства и только некоторых задач трёхмерного пространства, так как довольно трудно построить многогранник решений, который образуется в результате пересечения полупространств. Задачу пространства размерности больше трёх изобразить графически вообще невозможно.2Симплекс-метод решения задач линейного программирования.

Симплекс-метод – один из наиболее эффективных методов численного решения задач ЛП. Суть понятия «симплекс» заключается в следующем. Для тела в k -мерном пространстве симплексом называется множество, состоящее из k +1 вершин этого тела. Так, при k = 2, т.е. на плоскости, симплексом будут вершины треугольника; при k = 3 симплексом являются вершины четырехгранника, например тетраэдра, и т.д. Такое название методу дано по той причине, что в его основе лежит последовательный перебор вершин ОДЗП с целью определения координат той вершины, в которой функция цели имеет кстремальное значение.

Решение задачи с помощью симплекс-метода разбивается на два основных этапа.На первом этапе находят одно из решений, удовлетворяющее системе ограничений . Системы, в которых переменных больше, чем ограничений N > m, называются неопределенными. Они приводятся к определенным системам (N = m) путем приравнивания к нулю N-m каких-либо переменных. При этом остается система m уравнений с m неизвестными, которая имеет решение, если определитель системы отличен от нуля. В симплекс-методе вводится понятие базисных переменных, или базиса. Базисом называется любой набор из m таких переменных, что определитель, составленный из коэффициентов при этих переменных в m-ограничениях, отличен от нуля. Остальные N-m переменных называются небазисными, или свободными переменными. Если принять, что все небазисные переменные равны нулю, и решать систему ограничений относительно базисных переменных, то получим базисное решени

17.Симплекс метод и таблица.

Симплекс-метод — алгоритм решения оптимизационной задачи линейного программирования путём перебора вершин выпуклого многогранника в многомерном пространстве. Метод был разработан советским математиком Канторовичем Л. В. в 1939 годуСимплекс-метод – один из наиболее эффективных методов численного решения задач ЛП. Суть понятия «симплекс» заключается в следующем. Для тела в k -мерном пространстве симплексом называется множество, состоящее из k +1 вершин этого тела. Так, при k = 2, т.е. на плоскости, симплексом будут вершины треугольника; при k = 3 симплексом являются вершины четырехгранника, например тетраэдра, и т.д. Такое название методу дано по той причине, что в его основе лежит последовательный перебор вершин ОДЗП с целью определения координат той вершины, в которой функция цели имеет кстремальное значение.

Решение задачи с помощью симплекс-метода разбивается на два основных этапа.На первом этапе находят одно из решений, удовлетворяющее системе ограничений . Системы, в которых переменных больше, чем ограничений N > m, называются неопределенными. Они приводятся к определенным системам (N = m) путем приравнивания к нулю N-m каких-либо переменных. При этом остается система m уравнений с m неизвестными, которая имеет решение, если определитель системы отличен от нуля. В симплекс-методе вводится понятие базисных переменных, или базиса. Базисом называется любой набор из m таких переменных, что определитель, составленный из коэффициентов при этих переменных в m-ограничениях, отличен от нуля. Остальные N-m переменных называются небазисными, или свободными переменными. Если принять, что все небазисные переменные равны нулю, и решать систему ограничений относительно базисных переменных, то получим базисное решение.

18.Алгоритм решения задачи на ПК линейного программирования

1) Постановка задачи - необходимо четко определить цель задачи, дать словесное описание содержания задачи, выделить исходные данные для ее решения. Предложить общий подход к её решению, определиться какие результаты и в каком виде должны быть получены.

2) Построение математической модели - представление ее в виде формул, уравнений, соотношений, которые могут быть реализованы в компьютере.

3) Алгоритмизация - построение алгоритма.

4) Составление сценария работы на компьютере (этот этап мы пока будем опускать).

5) Написание задачи на языке программирования.

Программа должна быть универсальной (не зависящей от конкретного набора данных). Необходимо предусмотреть контроль вводимых данных. Необходимо повысить эффективность программы, т. е. уменьшить количество выполняемых операций и время работы программы.

6) Отладка и тестирование программы.

На этом этапе происходят выполнение алгоритма с помощью компьютера, поиск и исключение ошибок. При этом программисту приходится выполнять рутинную работу по проверке работы программы, поиску и исключению ошибок, и поэтому для сложных программ этот часто требует гораздо больше времени и сил, чем написание первоначального текста программы.

Программист должен составить тест - это специально подобранные исходные данные, в совокупности с результатами, которые должны получиться.

Отладка - это исправление ошибок - сложный и нестандартный процесс. Исходный план отладки заключается в том, чтобы оттестировать программу на составленных контрольных тестах.

7) Анализ полученных результатов.

Рассмотрим эти этапы на примере следующей задачи.

Задача. "Покупка в мазазине"

Человек делает в магазине покупки. Определите сколько денег у него останется после покупки в магазине перчаток стоимостью А руб., портфеля стоимостью B руб. и галстука стоимостью D руб. Все исходные данные задаются с клавиатуры.

1 этап. Постановка задачи

Исходные данные.

a - стоимость перчаток;

b - стоимость портфеля;

d - стоимост галстука;

dengi - количество денег у человека.

Все эти переменные будут вещественного типа.

Результат.

ostatok - количество денег, которое останется у человек (вещественный тип).

2 этап. Построение математической модели (метод решения)

ostatok = dengi - a - b - d

3 этап. Алгоритмизация.

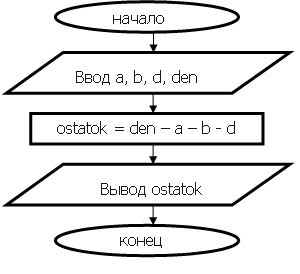
5 этап. Написание программы.

Program pokupka; Uses crt; Var a, b, d, den: real; ostatok: real; begin clrscr; write ('введите стоимость перчаток, портфеля и галстука '); readln (a, b, d); write ('введите количество имеющихся у вас денег '); readln (den); oststok := den - a - b - c; writeln ('после покупки у вас останется ', ostatok:5:2, 'руб. '); readln; end.

19.Постановка задач интерполирования и экстраполирования функций. Многочлен Лагранжа.

Аппроксимация функций заключается в приближенной замене заданной функции f(x) некоторой функцией  (x) так, чтобы отклонение функции  (x) от f(x) в заданной области было наименьшим. Функция  (х) при этом называется аппроксимирующей. Типичной задачей аппроксимации функций является задача интерполяции. Необходимость интерполяции функций в основном связана с двумя причинами:

1. Функция f(x) имеет сложное аналитическое описание, вызывающее определенные трудности при его использовании (например, f(x) является спецфункцией: гамма-функцией, эллиптической функцией и др.).

2. Аналитическое описание функции f(x) неизвестно, т. е. f(x) задана таблично. При этом необходимо иметь аналитическое описание, приближенно представляющее f(x) (например, для вычисления значений f(x) в произвольных точках, определения интегралов и производных от f(x) и т. п.)

Постановка задачи интерполяции

 

Простейшая задача интерполяции заключается в следующем. На отрезке [a, b] заданы n + 1 точки x_i = х₀, х₁, . . ., х_n, которые называются узлами интерполяции, и значения некоторой функции f(x)  в этих точках

f(x0) = y0, f(x1) =  y1,  . . ., f(xn) = yn.

(1)

Требуется построить функцию  (х) (интерполяционная функция), принадлежащую известному классу и принимающую в узлах интерполяции те же значения, что и f(x), т. е. такую, что

(x0) = y0, (x1) =  y1,  . . ., (xn) = yn.

(2)

Геометрически это означает, что нужно найти кривую y =  (х) некоторого определенного типа, проходящую через заданную систему точек M(x_i, y_i) (i = 0, 1, ..., n) (Рисунок 1).

 

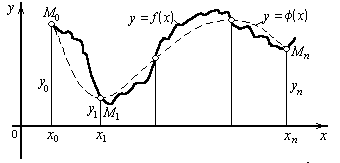
Рисунок 1

 

В такой общей постановке задача может иметь бесконечное множество решений или совсем не иметь решений.

Однако эта задача становится однозначной, если вместо произвольной функции  (х) искать полином  (х) (интерполяционныйполином) степени не выше n, удовлетворяющий условиям (2), т. е. такой, что

 (x0) = y0,  (x1) =  y1,  . . .,  (xn) = yn.

(3)

Полученную интерполяционную формулу

(4)

обычно используют для приближенного вычисления значений данной функции  (х) для значений аргумента х, отличных от узлов интерполяции. Такая операция называется интерполяцией функций.

Различают два вида интерполяции:

1. глобальная - соединение всех точек  (х) единым интерполяционным полиномом;

2. локальная - соединение точек отрезками прямой (по двум точкам), отрезками параболы (по трем точкам).

ЭКСТРАПОЛИРОВАНИЕ

экстраполяция, функции - продолжение функции за пределы ее области определения, при к-ром продолженная функция (как правило, аналитическая) принадлежит заданному классу. Э. функций обычно производится с помощью формул, в к-рых использована информация о поведении функции в нек-ром конечном наборе точек (узлах интерполяции), принадлежащих ее облает определения.  Понятие интерполирования функций употребляртся в качестве противопоставления понятию Э. функций (в узком смысле понимания этого термина), когда конструктивно восстанавливаются (быть может, приближенно) значения функций в областях их определений.  Пример. Если заданы значения функции   в узлах   то интерполяционныймногочлен Лагранжа L_n(x)(см. Лагранжа интерполяционная формула), будучи определен на всей числовой оси   является, в частности, Э. функции f вне отрезка [ а, b]в классе многочленов степени не выше п.  Иногда при Э. функций используется не вся ее область определения, а только ее часть, т. е. фактически производится Э. значений сужения заданной функции на указанной части. В этом случае экстраполяционные формулы дают, в частности, значения (вообще говоря, приближенные) функции в соответствующих точках ее области определения. Именно таким образом часто поступают при решении практич. задач, когда вне рассматриваемой части области определения нек-рой функции отсутствует достаточная информация, необходимая для вычисления ее значений.

Интерполяцио́нный многочле́н Лагра́нжа — многочлен минимальной степени, принимающий данные значения в данном наборе точек. Для n + 1 пар чисел  , где все x_i различны, существует единственный многочленL(x) степени не более n, для которого L(x_i) = y_i.

В простейшем случае (n = 1) — это линейный многочлен, график которого — прямая, проходящая через две заданные точки.

20.Интерполяционные многочлены Ньютона. Конечные разности

Интерполяционным многочленом Ньютона называется многочлен

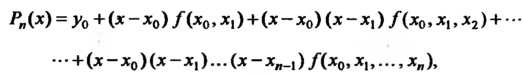(31.13)

В котором I - разделенные разности различных порядков.

Этот многочлен удовлетворяет условиям

Интерполяционной формулой Ньютона называется формула

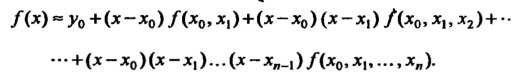(31.14)

Замечание 1. Поскольку любой Член многочлена Ньютона зависит только от Первых узлов интерполяции и от значений функции в этих узлах, добавление новых узлов вызывает в формуле (31.13) лишь добавление новых членов без изменения первоначальных. Это является существенным преимуществом многочлена Ньютона по сравнению с многочленом Лагранжа.

Замечание 2. В силу единственности интерполяционного многочлена  Степени интерполяционный многочлен Ньютона перегруппировкой членов можно преобразовать в интерполяционный многочлен Лагранжа и обратно.

В случае равноотстоящих узлов интерполяции

| из формулы (31.14) с учетом (31.12) получается интерполяционная формула Ньютона для «интерполирования вперед»:

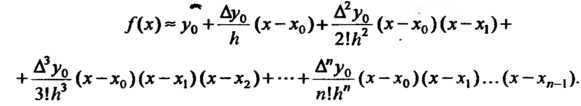(31.15)

Формула (31.15) удобна при интерполировании функций для значений х, близких к наименьшему узлу

Интерполяционная формула Ньютона для «интерполирования назад»:

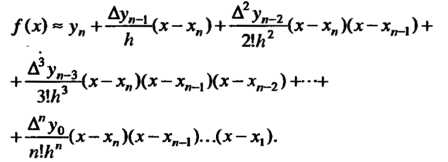(31.16)

Формула (31.16) удобна при интерполировании функций для значений х, близких к наибольшему узлу

Замечание 3. В формуле (31.15) в коэффициенты многочлена входят конечные разности различных порядков, принадлежащие верхней (нисходящей) строке таблицы разностей (см. табл. 31.1). В формуле (31.16) в коэффициенты многочлена входят разности различных порядков, принадлежащие нижней (восходящей) строке таблицы разностей.

Пример 31.4. Найти интерполяционный многочлен Ньютона для функции , если известны ее значения:

В данном случае Отметим, что

Узлы не являются равноотстоящими (так как ). Интерполяционный

Многочлен (31.13) при С учетом равенств (31.11) принимает вид

Вычисляем разделенные разности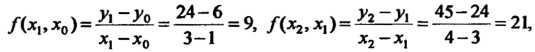   

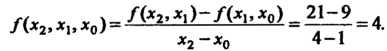
Подставляя в выражение для Соответствующие значения, находим интерпо

Ляционный многочлен Ньютона

Замечание 4. Раскрывая скобки и группируя члены, получаем

Пример 31.5. Найти интерполяционный многочлен Ньютона для функции По ее значениям в точках И вычислить И

Вычислим сначала значения функции в данных равноотстоящих узлах:

Составим таблицу разностей различных порядков (табл. 31.3).

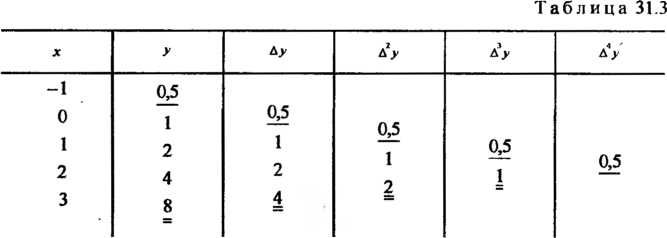
Числа, подчеркнутые одной чертой входят в интерполяционную формулу Ньютона для «интерполирования вперед». Многочлен в правой части формулы (31.15) в данном случае Принимает вид

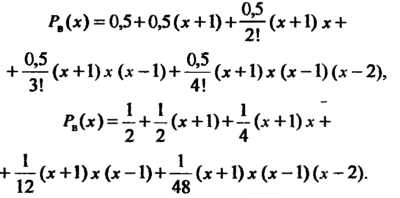
С помощью этого многочлена вычислим значение функции При

(значение аргумента ближе к Подставляя значение

В формулу (I), находим

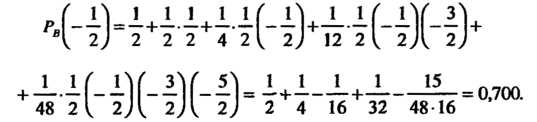
Числа табл. 31.3, подчеркнутые двумя чертами (и число 0,5 в столбце I, входят в интерполяционную формулу Ньютона для «интерполирования назад». Многочлен в правой части формулы (31.16) в данном случае принимает ввд

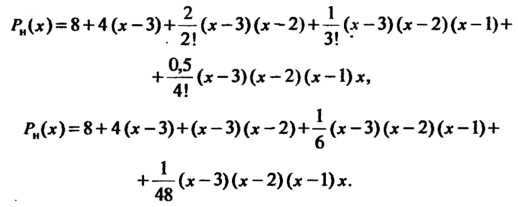
С помощью многочлена (II) вычислим значение данной функции При

(это значение аргумента ближе к ). Подставляя значение В

Формулу (II), получаем

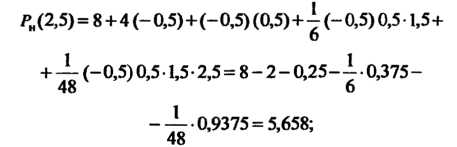
Следовательно,

Замечание 5. Многочлены (I) и (II) различаются лишь формой записи. Действительно, раскрывая скобки и приводя подобные члены, получаем 

Damira