Nagima

4 jok

1 Дайте определение статической и динамической системам, непрерывной и дискретной системам

Статическая система — это такая система автоматического регулирования, в которой ошибка регулирования стремится к постоянному значению при входном воздействии, стремящемся к некоторому постоянному значению. Иными словами статическая система не может обеспечить постоянства управляемого параметра при переменной нагрузке.

Зависимость между значением управляемого параметра и величиной внешнего воздействия (нагрузкой) на объект управления. По виду зависимости между значением управляемого параметра и нагрузкой системы делят на статические и динамические. Зависимость динамической ошибки (q) от времени (t) для систем в установившемся режиме имеет вид q(t) = x(t) — y(t), где x(t) — сигнал управления, y(t) — выходная характеристика.

При установившихся значениях сигнала управления и выходной характеристики ошибка системы q(уст) = x(уст) — y(уст). В зависимости от значения q(уст) и определяют тип системы.

Под динамической системой понимают любой объект или процесс, для которого однозначно определено понятие состояния как совокупности некоторых величин в данный момент времени и задан закон, который описывает изменение (эволюцию) начального состояния с течением времени. Этот закон позволяет по начальному состоянию прогнозировать будущее состояние динамической системы, его называют законом эволюции. Динамические системы - это механические, физические, химические и биологические объекты, вычислительные процессы и процессы преобразования информации, совершаемые в соответствии с конкретными алгоритмами. Описания динамических систем для задания закона эволюции также разнообразны: с помощью дифференциальных уравнений, дискретных отображений, теории графов, теории марковских цепей и т.д. Выбор одного из способов описания задает конкретный вид математической модели соответствующей динамической системы [2].

В системах непрерывного действия (непрерывных системах) существуют только непрерывные сигналы, являющиеся непре­рывными функциями времени. Все звенья этих САУ— звенья непрерывного действия, т. е. их входные и выходные ве­личины представляют собой непрерывные сигналы.

САУ дискретного дёйствия (дискретной САУ) называется сис­тема, в которой хотя бы одна величина представляет собой диск­ретный сигнал. Дискретный сигнал изменяется во времени диск­ретно, скачками . Существуют дискретные САУ, в которых имеются только дискретные сигналы. Такие системы состоят полностью из звеньев дискретного действия, входные и выходные величины, которых являются дискретными. Однако в большинстве дискретных систем имеются как дискретные, так и непрерывные сигналы. В состав таких систем наряду со звень­ями непрерывного и дискретного действия входят звенья, преоб­разующие непрерывные сигналы в дискретные, и звенья, осу­ществляющие обратное преобразование.

Преобразование непрерывного сигнала в дискретный называ­ется квантованием сигнала. Существуют два основных вида квантования: по уровню и по времени .

Сигнал, квантованный но уровню, может принимать только впол­не определенные дискретные значения, соответствующие уровням, показанным на рис. 11-1, б, горизонтальными линиями. Сигнал, квантованный по времени, изменяется скачком в фиксированные моменты времени, показанные на рис. 11-1, в вертикальными ли­ниями.

 

На рис,г изображен сигнал, квантованный и по уровню и по времени.

В соответствии с названными выше видами квантования САУ дискретного действия делятся на три типа: релейные, им­пульсные и цифровые.' Релейные САУ — это системы с квантованием по уровню, импульсные — с квантованием по времени, а цифровые — с применением обоих видов кван­тования х.           

2. Что понимается под объектом управления и его моделью?

Существует два способа получения модели объекта управления: формальный и физический. При формальном подходе используют модель типа "черный ящик", в которой не содержится информация о физических процессах, происходящих в объекте, или о его структуре. Синтез формальной модели сводится к выбору одной из небольшого числа моделей, описанных ниже, и идентификации ее параметров.

1. 3 Представьте блок-схему системы параметрической идентификации с адаптивной моделью.

Модель – приближённая и объект изменяется во времени. Улучшение модели называется идентификацией (повышение её точности). Идентификация имеет 2 стороны:

структурная;

параметрическая.

Под структурной идентификацией понимается приближение структуры модели к реальной так, чтобы она наилучшим образом отражала объект. Так как объекты могут быть самыми различными (механическими, экологическими и др.) нельзя придумать формальных методов структурной идентификации.параметрическая идентификация – это улучшение значений параметров модели с целью повышения точности модели. Точность всегда понимается как разность между прогнозируемым и тем, что получаем.

Адаптация означает подстройку параметров регулятора, его самообучение. Параметры регулятора зависят от параметров объекта и обычно выражаются через них. Изначально параметры объекта не всегда известны с достаточной степенью точности или “плывут” во времени, что и вынуждает прибегать к адаптации. Поэтому адаптации – изменению характеристик регулятора – обычно предшествует процедура уточнения характеристик объекта по результатам измерения входных и выходных величин, которая называется идентификацией.

5 Какими характеристиками определяются дискретные системы идентификации?

Функция fvtool по существу представляет собой графическую среду, предназначенную для анализа и визуализации характеристик дискретных систем (Filter Visualization Tool). Однако, в отличие от других графических сред пакета, fvtool действительно является функцией, поскольку при вызове требует наличия входных параметров — коэффициентов полиномов числителя и знаменателя функции передачи анализируемого фильтра. Существенным достоинством данной функции является возможность одновременного просмотра характеристик нескольких фильтров

Динамическая система представляет собой математическую модель некоторого объекта, процесса или явления.

Динамическая система также может быть представлена как система, обладающая состоянием. При таком подходе, динамическая система описывает (в целом) динамику некоторого процесса, а именно: процесс перехода системы из одного состояния в другое. Фазовое пространство системы — совокупность всех допустимых состояний динамической системы. Таким образом, динамическая система характеризуется своим начальным состоянием и законом, по которому система переходит из начального состояния в другое.

6 Представьте схему дискретной системы с моделью объекта

Представление математического описания объектов управления мехатронных систем в пакете Control System Toolbox [14]. Пакет Control System Toolbox предназна­чен для моделирования, анализа и проектирования непрерывных и дискретных систем автома­тического управления. Функ­ции пакета реализуют методы исследования динамических систем, основанные на использовании передаточных функций и моделей для переменных состояния. Частотные и временные характеристики, нули и полюсы системы легко вычисляются и отображаются в виде гра­фиков и диаграмм. Рассмотрим способы математического описания линейных осистем, которые предоставляются пакетом расширения Control System Toolbox (CST). Исследование систем автоматического управления начинается с создания математической модели. В пакете CST линейные модели могут быть представлены в четырех формах:  - передаточная функция (tf);  - нули, полюса и коэффициент усиления (zpk);  - пространство состояния (ss);  - системная функция (frd). 

Математическое описание непрерывных объектов управления в мехатронных системах. Для того, чтобы исследовать динамику объекта управления необходимо располагать его математическим описанием, т. е. системой дифференциальных уравнений, характеризующих зависимости координат и внешних воздействий друг от друга.  Наиболее распространенными способами математического описания мехатронных систем являются: 

• дифференциальные уравнения, записываемые в той или иной форме; 

• уравнения состояний - система дифференциальных уравнений, записанных в нормальной форме Коши;

• передаточные функции;

• системные функции (амплитулно-частотные, фазо-частотные, амплитудно-фазовые характеристики);

7 Определите условия устойчивости процессов идентификации дискретной системы.

Поскольку характеристический полином произвольного порядка с действительными коэффициентами может быть разложен на произведение полиномов первой и второй степени, то сложный алгоритм, определяемый передаточной функцией общего вида, может быть сведен к последовательному выполнению дискретных алгоритмов первого и второго порядков, свойства которых рассмотрены выше.

Кроме того, Z-передаточную функцию звена произвольного порядка в соответствии с теоремой Хевисайда можно разложить на элементарные слагаемые [7], к каждому из которых применимы сформулированные выше критерии устойчивости и качества:

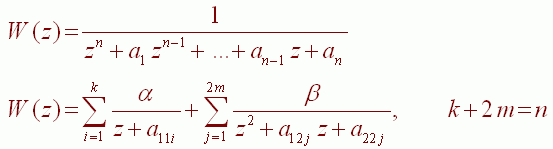
Для того чтобы этот объект был устойчивым, устойчивыми должны быть элементарные звенья, составляющие эквивалентную схему объекта. Для упрощения изложения принято, что характеристический Z-полином не содержит кратных корней.

Т.о. достаточное условие устойчивости дискретного звена произвольного порядка: коэффициенты характеристических Z-полиномов элементарных звеньев, составляющих произвольное дискретное звено, должны располагаться внутри гиперпараллепипеда в гиперпространстве, т.е. |а_11i| < 1, |а_12i| < 0.5 и |а_22j| < 0.5 для всех i и j, т.е. 0 < i < k+1, 0 < j < 2m+1.

Необходимое условие устойчивости : |а_11i| < 1, |а_12j| < 2 и |а_22j| < 1 для всех i и j, т.е. 0 < i < k+1, 0 < j < 2m+1.

Аналогично можно ввести и критерий качества переходного процесса дискретного звена произвольного порядка: коэффициенты характеристических Z-полиномов элементарных звеньев, составляющих произвольное дискретное звено, должны располагаться внутри гиперпараллепипеда в гиперпространстве, т.е. |а_11i| < 0.5, |а_12j| < 0.35 и |а_22ja22j| < 0.35 для всех i и j, т.е. 0 < i < k+1, 0 < j < 2m+1.

Конечно, эти критерии не так удобны, как те, что сформулированы для дискретных звеньев первого и второго порядков, поскольку требует предварительного разложения характеристического Z-передаточной функции на простые слагаемые.

Отметим, что поскольку характеристический Z-полином дискретного звена произвольного порядка может быть разложен на элементарные сомножители первого и второго порядка, то при этом достаточное и необходимое условия, как устойчивости, так и качества будут иметь аналогичный вид.

8 Какими уравнениями описывается математическая модель объекта управления с учетом алгоритмов общего параметра?

Математи́ческая моде́ль  это математическое представление реальности^[1]. Является частным случаем понятия модели, как системы, исследование которой позволяет получать информацию о некоторой другой системе

Математические модели могут быть детерменированными и стохастическими.

Детерменированные модели- это модели, в которых установлено взаимно-однозначное соответствие между переменными описывающими объект или явления.

Такой подход основан на знании механизма функционирования объектов. Часто моделируемый объект сложен и расшифровка его механизма может оказаться очень трудоемкой и длинной во времени. В этом случае поступают следующим образом: на оригинале проводят эксперименты, обрабатывают полученные результаты и, не вникая в механизм и теорию моделируемого объекта с помощью методов математической статистики и теории вероятности, устанавливают связи между переменными, описывающими объект. В этом случае получают стахостическую модель. В стахостической модели связь между переменными носит случайный характер, иногда это бывает принципиально. Воздействие огромного количества факторов, их сочетание приводит к случайному набору переменных описывающих объект или явление. По характеру режимов модель бывают статистическими идинамическими.

Статистическая модель включает описание связей между основными переменными моделируемого объекта в установившемся режиме без учета изменения параметров во времени.

В динамической модели описываются связи между основными переменными моделируемого объекта при переходе от одного режима к другому.

Модели бывают дискретными и непрерывными, а также смешанного типа. В непрерывных переменные принимают значения из некоторого промежутка, в дискретных переменные принимают изолированные значения.

Линейные модели- все функции и отношения, описывающие модель линейно зависят от переменных и не линейные в противном случае.