Вариант № 3713330

1. B 13 . Объем пра­виль­ной ше­сти­уголь­ной пи­ра­ми­ды 6. Сто­ро­на ос­но­ва­ния равна 1. Най­ди­те бо­ко­вое ребро.

Ре­ше­ние.

Пло­щадь ос­но­ва­ния равна

 

.

Из фор­му­лы для объ­е­ма пи­ра­ми­ды най­дем вы­со­ту:

 

.

В пра­виль­ном ше­сти­уголь­ни­ке сто­ро­на равна ра­ди­у­су опи­сан­ной окруж­но­сти, по­это­му най­дем бо­ко­вое ребро пи­ра­ми­ды по тео­ре­ме Пи­фа­го­ра:

 

.

Ответ: 7.

Ответ: 7

2. B 13 .

Конус впи­сан в шар. Ра­ди­ус ос­но­ва­ния ко­ну­са равен ра­ди­у­су шара. Объем ко­ну­са равен 6. Най­ди­те объем шара.

 

Ре­ше­ние.

 

. .

 

Ответ: 24.

Ответ: 24

3. B 13 . Ра­ди­у­сы трех шаров равны 6, 8 и 10. Най­ди­те ра­ди­ус шара, объем ко­то­ро­го равен сумме их объ­е­мов.

Ре­ше­ние.

Объем та­ко­го шара

 

,

от­ку­да по­лу­чим, что .

Ответ: 12.

Ответ: 12

4. B 13 .

Най­ди­те объем пра­виль­ной ше­сти­уголь­ной приз­мы, все ребра ко­то­рой равны .

 

Ре­ше­ние.

Объем приз­мы равен про­из­ве­де­нию пло­ща­ди ос­но­ва­ния на вы­со­ту. Вы­со­той пра­виль­ной приз­мы яв­ля­ет­ся ее бо­ко­вое ребро. Ос­но­ва­ние приз­мы — пра­виль­ный ше­сти­уголь­ник. Пло­щадь пра­виль­но­го ше­сти­уголь­ни­ка со сто­ро­ной вы­чис­ля­ет­ся по фор­му­ле . Сле­до­ва­тель­но,

 

 

 

Ответ: 13,5.

Ответ: 13,5

5. B 13 . Диа­метр ос­но­ва­ния ко­ну­са равен 6, а угол при вер­ши­не осе­во­го се­че­ния равен 90°. Вы­чис­ли­те объем ко­ну­са, де­лен­ный на .

Ре­ше­ние.

В тре­уголь­ни­ке, об­ра­зо­ван­ном ра­ди­у­сом ос­но­ва­ния r, вы­со­той h и об­ра­зу­ю­щей ко­ну­са l, углы при об­ра­зу­ю­щей равны, по­это­му вы­со­та ко­ну­са равна ра­ди­у­су его ос­но­ва­ния: h = r. Тогда объем ко­ну­са, де­лен­ный на вы­чис­ля­ет­ся сле­ду­ю­щим об­ра­зом:

 

Ответ: 9.

Ответ: 9

6. B 13 . Ребра пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да, вы­хо­дя­щие из одной вер­ши­ны, равны 1, 2, 3. Най­ди­те его пло­щадь по­верх­но­сти.

Ре­ше­ние.

Пло­щадь по­верх­но­сти пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да равна удво­ен­ной сумме по­пар­ных про­из­ве­де­ний его из­ме­ре­ний

 

.

Ответ: 22.

Ответ: 22

7. B 13 . Най­ди­те объем части ци­лин­дра, изоб­ра­жен­ной на ри­сун­ке. В от­ве­те ука­жи­те .

Ре­ше­ние.

Объем дан­ной части ци­лин­дра равен

 

.

Ответ: 937,5.

Ответ: 937,5

8. B 13 . 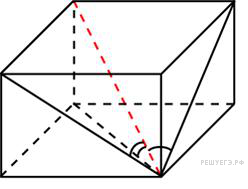Диа­го­наль пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да равна и об­ра­зу­ет углы 30 , 30 и 45 с плос­ко­стя­ми гра­ней па­рал­ле­ле­пи­пе­да. Най­ди­те объем па­рал­ле­ле­пи­пе­да.

Ре­ше­ние.

Ребро па­рал­ле­ле­пи­пе­да на­про­тив угла в равно , по­сколь­ку об­ра­зу­ет с за­дан­ной диа­го­на­лью и диа­го­на­лью одной из гра­ней рав­но­бед­рен­ный тре­уголь­ник. Два дру­гие ребра по по­стро­е­нию лежат в пря­мо­уголь­ных тре­уголь­ни­ках на­про­тив угла в и равны, по­это­му по­ло­ви­не диа­го­на­ли. Тогда объем па­рал­ле­ле­пи­пе­да:

 

Ответ: 4.

Ответ: 4

9. B 13 . Ос­но­ва­ни­ем пи­ра­ми­ды слу­жит пря­мо­уголь­ник, одна бо­ко­вая грань пер­пен­ди­ку­ляр­на плос­ко­сти ос­но­ва­ния, а три дру­гие бо­ко­вые грани на­кло­не­ны к плос­ко­сти ос­но­ва­ния под углом 60 . Вы­со­та пи­ра­ми­ды равна 6. Най­ди­те объем пи­ра­ми­ды.

Ре­ше­ние.

В тре­уголь­ни­ках и сто­ро­на — общая, и , по­это­му эти тре­уголь­ни­ки равны; тре­уголь­ник — рав­но­сто­рон­ний, и . Тогда объем пи­ра­ми­ды

 

Ответ: 48.

Ответ: 48

10. B 13 . В пра­виль­ной че­ты­рех­уголь­ной пи­ра­ми­де вы­со­та равна 6, бо­ко­вое ребро равно 10. Най­ди­те ее объем.

Ре­ше­ние.

По тео­ре­ме Пи­фа­го­ра най­дем, что по­ло­ви­на диа­го­на­ли ос­но­ва­ния равна 8. Тогда диа­го­наль ос­но­ва­ния равна 16, а сто­ро­на –   и пло­щадь

 

Тогда объем пи­ра­ми­ды

Ответ: 256.

Ответ: 256