Задание В12

Вариант № 3711725

1. B 12 . Дат­чик скон­стру­и­ро­ван таким об­ра­зом, что его ан­тен­на ловит ра­дио­сиг­нал, ко­то­рый затем пре­об­ра­зу­ет­ся в элек­три­че­ский сиг­нал, из­ме­ня­ю­щий­ся со вре­ме­нем по за­ко­ну , где – время в се­кун­дах, ам­пли­ту­да В, ча­сто­та /с, фаза . Дат­чик на­стро­ен так, что если на­пря­же­ние в нeм не ниже чем В, за­го­ра­ет­ся лам­поч­ка. Какую часть вре­ме­ни (в про­цен­тах) на про­тя­же­нии пер­вой се­кун­ды после на­ча­ла ра­бо­ты лам­поч­ка будет го­реть?

Ре­ше­ние.

За­да­ча сво­дит­ся к ре­ше­нию урав­не­ния при за­дан­ных зна­че­ни­ях ам­пли­ту­ды сиг­на­ла, ча­сто­ты и фазы:

 

 

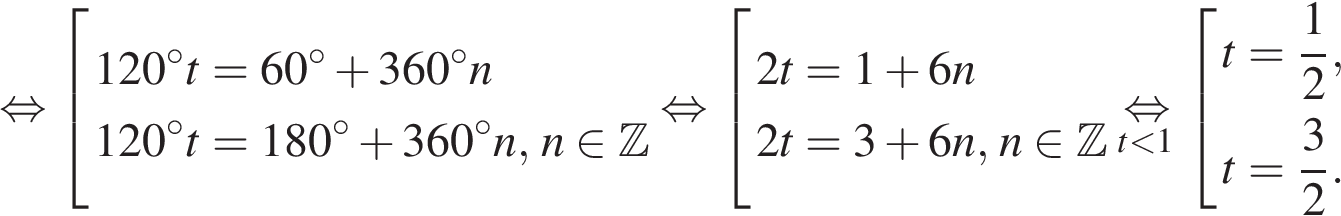
На про­тя­же­нии пер­вой се­кун­ды лам­поч­ка будет го­реть с, то есть % вре­ме­ни.

Ответ: 50.

Ответ: 50

2. B 12 . Де­та­лью не­ко­то­ро­го при­бо­ра яв­ля­ет­ся вра­ща­ю­ща­я­ся ка­туш­ка. Она со­сто­ит из трeх од­но­род­ных со­ос­ных ци­лин­дров: цен­траль­но­го мас­сой кг и ра­ди­у­са см, и двух бо­ко­вых с мас­са­ми кг и с ра­ди­у­са­ми . При этом мо­мент инер­ции ка­туш­ки от­но­си­тель­но оси вра­ще­ния, вы­ра­жа­е­мый в , даeтся фор­му­лой При каком мак­си­маль­ном зна­че­нии мо­мент инер­ции ка­туш­ки не пре­вы­ша­ет пре­дель­но­го зна­че­ния 625 ? Ответ вы­ра­зи­те в сан­ти­мет­рах.

Ре­ше­ние.

За­да­ча сво­дит­ся к на­хож­де­нию наи­боль­ше­го ре­ше­ния не­ра­вен­ства км при за­дан­ных зна­че­ни­ях па­ра­мет­ров , и :

 

Решая квад­рат­ное не­ра­вен­ство ме­то­дом ин­тер­ва­лов, по­лу­чим . Наи­боль­шее ре­ше­ние двой­но­го не­ра­вен­ства — число 5.

Ответ: 5.

Ответ: 5

3. B 12 . Если до­ста­точ­но быст­ро вра­щать ведeрко с водой на верeвке в вер­ти­каль­ной плос­ко­сти, то вода не будет вы­ли­вать­ся. При вра­ще­нии ведeрка сила дав­ле­ния воды на дно не остаeтся по­сто­ян­ной: она мак­си­маль­на в ниж­ней точке и ми­ни­маль­на в верх­ней. Вода не будет вы­ли­вать­ся, если сила еe дав­ле­ния на дно будет по­ло­жи­тель­ной во всех точ­ках тра­ек­то­рии кроме верх­ней, где она может быть рав­ной нулю. В верх­ней точке сила дав­ле­ния, вы­ра­жен­ная в нью­то­нах, равна , где – масса воды в ки­ло­грам­мах, ско­рость дви­же­ния ведeрка в м/с, – длина верeвки в мет­рах, g – уско­ре­ние сво­бод­но­го па­де­ния (счи­тай­те м/с ). С какой наи­мень­шей ско­ро­стью надо вра­щать ведeрко, чтобы вода не вы­ли­ва­лась, если длина верeвки равна 40 см? Ответ вы­ра­зи­те в м/с.

Ре­ше­ние.

За­да­ча сво­дит­ся к ре­ше­нию не­ра­вен­ства при за­дан­ной длине верёвки м:

 

Ответ: 2.

Ответ: 2

4. B 12 . Рас­сто­я­ние (в км) от на­блю­да­те­ля, на­хо­дя­ще­го­ся на не­боль­шой вы­со­те ки­ло­мет­ров над землeй, до на­блю­да­е­мой им линии го­ри­зон­та вы­чис­ля­ет­ся по фор­му­ле , где (км) — ра­ди­ус Земли. С какой вы­со­ты го­ри­зонт виден на рас­сто­я­нии 4 ки­ло­мет­ра? Ответ вы­ра­зи­те в ки­ло­мет­рах.

Ре­ше­ние.

За­да­ча сво­дит­ся к ре­ше­нию урав­не­ний при за­дан­ном зна­че­нии R:

 

 

При­ме­ча­ние. За­ме­тим, что по­лу­чен­ная ве­ли­чи­на равна 1,25 метра, т. е. со­от­вет­ству­ет уров­ню глаз ре­бен­ка.

Ответ: 0,00125.

Ответ: 0,00125

5. B 12 . Ло­ка­тор ба­ти­ска­фа, рав­но­мер­но по­гру­жа­ю­ще­го­ся вер­ти­каль­но вниз, ис­пус­ка­ет уль­тра­зву­ко­вые им­пуль­сы ча­сто­той 749 МГц. Ско­рость спус­ка ба­ти­ска­фа, вы­ра­жа­е­мая в м/с, опре­де­ля­ет­ся по фор­му­ле , где м/с – ско­рость звука в воде, – ча­сто­та ис­пус­ка­е­мых им­пуль­сов (в МГц), – ча­сто­та отражeнного от дна сиг­на­ла, ре­ги­стри­ру­е­мая приeмни­ком (в МГц). Опре­де­ли­те наи­боль­шую воз­мож­ную ча­сто­ту от­ра­жен­но­го сиг­на­ла , если ско­рость по­гру­же­ния ба­ти­ска­фа не долж­на пре­вы­шать 2 м/с.

Ре­ше­ние.

За­да­ча сво­дит­ся к ре­ше­нию не­ра­вен­ства м/с при из­вест­ных зна­че­ни­ях м/с – ско­ро­сти звука в воде и МГц – ча­сто­ты ис­пус­ка­е­мых им­пуль­сов:

 

МГц.

Ответ: 751.

Ответ: 751

6. B 12 . Ав­то­мо­биль, дви­жу­щий­ся в на­чаль­ный мо­мент вре­ме­ни со ско­ро­стью м/с, начал тор­мо­же­ние с по­сто­ян­ным уско­ре­ни­ем м/с². За – се­кунд после на­ча­ла тор­мо­же­ния он прошёл путь (м). Опре­де­ли­те время, про­шед­шее от мо­мен­та на­ча­ла тор­мо­же­ния, если из­вест­но, что за это время ав­то­мо­биль про­ехал 30 мет­ров. Ответ вы­ра­зи­те в се­кун­дах.

Ре­ше­ние.

Най­дем, за какое время , про­шед­шее от мо­мен­та на­ча­ла тор­мо­же­ния, ав­то­мо­биль про­едет 30 мет­ров:

 

.

Зна­чит, через 2 се­кун­ды после на­ча­ла тор­мо­же­ния ав­то­мо­биль про­едет 30 мет­ров.

 

Ответ: 2.

Ответ: 2

7. B 12 . После дождя уро­вень воды в ко­лод­це может по­вы­сить­ся. Маль­чик из­ме­ря­ет время па­де­ния не­боль­ших ка­меш­ков в ко­ло­дец и рас­счи­ты­ва­ет рас­сто­я­ние до воды по фор­му­ле , где – рас­сто­я­ние в мет­рах, – время па­де­ния в се­кун­дах. До дождя время па­де­ния ка­меш­ков со­став­ля­ло 0,6 с. На сколь­ко дол­жен под­нять­ся уро­вень воды после дождя, чтобы из­ме­ря­е­мое время из­ме­ни­лось на 0,2 с? Ответ вы­ра­зи­те в мет­рах.

Ре­ше­ние.

Пусть – рас­сто­я­ние до воды до дождя, – рас­сто­я­ние до воды после дождя. После дождя уро­вень воды в ко­лод­це по­вы­сит­ся, рас­сто­я­ние до воды умень­шит­ся, и время па­де­ния умень­шит­ся, ста­нет рав­ным с. Уро­вень воды под­ни­мет­ся на мет­ров.

 

Ответ: 1.

Ответ: 1

8. B 12 . Вы­со­та над землeй под­бро­шен­но­го вверх мяча ме­ня­ет­ся по за­ко­ну , где – вы­со­та в мет­рах, – время в се­кун­дах, про­шед­шее с мо­мен­та брос­ка. Сколь­ко се­кунд мяч будет на­хо­дить­ся на вы­со­те не менее трeх мет­ров?

Ре­ше­ние.

Опре­де­лим мо­мен­ты вре­ме­ни, когда мяч на­хо­дил­ся на вы­со­те ровно три метра. Для этого решим урав­не­ние :

 

Про­ана­ли­зи­ру­ем по­лу­чен­ный ре­зуль­тат: по­сколь­ку по усло­вию за­да­чи мяч бро­шен снизу вверх, это озна­ча­ет, что в мо­мент вре­ме­ни (с) мяч на­хо­дил­ся на вы­со­те 3 метра, дви­га­ясь снизу вверх, а в мо­мент вре­ме­ни (с) мяч на­хо­дил­ся на этой вы­со­те, дви­га­ясь свер­ху вниз. По­это­му он на­хо­дил­ся на вы­со­те не менее трёх мет­ров 1,2 се­кун­ды.

 

Ответ: 1,2.

Ответ: 1,2

9. B 12 . Мо­то­цик­лист, дви­жу­щий­ся по го­ро­ду со ско­ро­стью  км/ч, вы­ез­жа­ет из него и сразу после вы­ез­да на­чи­на­ет раз­го­нять­ся с по­сто­ян­ным уско­ре­ни­ем км/ч . Рас­сто­я­ние от мо­то­цик­ли­ста до го­ро­да, из­ме­ря­е­мое в ки­ло­мет­рах, опре­де­ля­ет­ся вы­ра­же­ни­ем . Опре­де­ли­те наи­боль­шее время, в те­че­ние ко­то­ро­го мо­то­цик­лист будет на­хо­дить­ся в зоне функ­ци­о­ни­ро­ва­ния со­то­вой связи, если опе­ра­тор га­ран­ти­ру­ет по­кры­тие на рас­сто­я­нии не далее чем в 30 км от го­ро­да. Ответ вы­ра­зи­те в ми­ну­тах.

Ре­ше­ние.

Мо­то­цик­лист будет на­хо­дить­ся в зоне функ­ци­о­ни­ро­ва­ния со­то­вой связи, если км. За­да­ча сво­дит­ся к на­хож­де­нию наи­боль­ше­го ре­ше­ния не­ра­вен­ства км при за­дан­ных зна­че­ни­ях па­ра­мет­ров и :

 

Учи­ты­вая то, что время – не­от­ри­ца­тель­ная ве­ли­чи­на, по­лу­ча­ем ч, то есть мин.

 

Ответ: 30.

Ответ: 30

10. B 12 . Ско­рость ав­то­мо­би­ля, раз­го­ня­ю­ще­го­ся с места стар­та по пря­мо­ли­ней­но­му от­рез­ку пути дли­ной км с по­сто­ян­ным уско­ре­ни­ем км/ч ², вы­чис­ля­ет­ся по фор­му­ле . Опре­де­ли­те наи­мень­шее уско­ре­ние, с ко­то­рым дол­жен дви­гать­ся ав­то­мо­биль, чтобы, про­ехав один ки­ло­метр, при­об­ре­сти ско­рость не менее 100 км/ч. Ответ вы­ра­зи­те в км/ч².