Вариант № 3706585

1. B 10 . Пря­мо­уголь­ный па­рал­ле­ле­пи­пед опи­сан около ци­лин­дра, ра­ди­ус ос­но­ва­ния ко­то­ро­го равен 4. Объем па­рал­ле­ле­пи­пе­да равен 16. Най­ди­те вы­со­ту ци­лин­дра.

Ре­ше­ние.

Вы­со­та па­рал­ле­ле­пи­пе­да равна вы­со­те впи­сан­но­го в него ци­лин­дра. Ос­но­ва­ни­ем па­рал­ле­ле­пи­пе­да яв­ля­ет­ся квад­рат, сто­ро­на ко­то­ро­го в два раза боль­ше ра­ди­у­са впи­сан­ной в него окруж­но­сти. По­это­му сто­ро­на ос­но­ва­ния равна 8, а пло­щадь ос­но­ва­ния равна 64. Тогда вы­со­та ци­лин­дра равна

 

.

Ответ: 0,25.

Ответ: 0,25

2. B 10 . Най­ди­те пло­щадь по­верх­но­сти мно­го­гран­ни­ка, изоб­ра­жен­но­го на ри­сун­ке (все дву­гран­ные углы пря­мые).

Ре­ше­ние.

Пло­щадь по­верх­но­сти тела равна сумме по­верх­но­стей трех со­став­ля­ю­щих ее па­рал­ле­ле­пи­пе­дов с реб­ра­ми 2, 3, 5; 1, 3, 5 и 2, 2, 3:

 

.

Ответ: 140.

Ответ: 140

3. B 10 . Около шара опи­сан ци­линдр, пло­щадь по­верх­но­сти ко­то­ро­го равна 18. Най­ди­те пло­щадь по­верх­но­сти шара.

Ре­ше­ние.

По по­стро­е­нию ра­ди­у­сы шара и ос­но­ва­ния ци­лин­дра равны. Пло­щадь по­верх­но­сти ци­лин­дра, с ра­ди­у­сом ос­но­ва­ния r и вы­со­той 2r равна

 

.

Пло­щадь по­верх­но­сти шара ра­ди­у­са равна , то есть в 1,5 раза мень­ше пло­ща­ди по­верх­но­сти ци­лин­дра. Сле­до­ва­тель­но, пло­щадь по­верх­но­сти шара равна 12.

 

Ответ: 12.

Ответ: 12

4. B 10 . 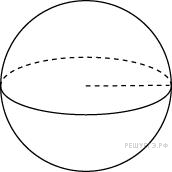Во сколь­ко раз уве­ли­чит­ся объем шара, если его ра­ди­ус уве­ли­чить в три раза?

Ре­ше­ние.

Объем шара ра­ди­у­са   равен

 

.

При уве­ли­че­нии ра­ди­у­са втрое, объем шара уве­ли­чит­ся в 27 раз.

Ответ: 27.

Ответ: 27

5. B 10 . 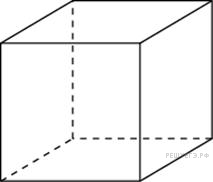Если каж­дое ребро куба уве­ли­чить на 1, то его объем уве­ли­чит­ся на 19. Най­ди­те ребро куба.

Ре­ше­ние.

Объем куба с реб­ром равен . Уве­ли­че­ние объ­е­ма равно 19:

 

Решим урав­не­ние:

 

Тем самым, .

Ответ: 2.

Ответ: 2

6. B 10 . 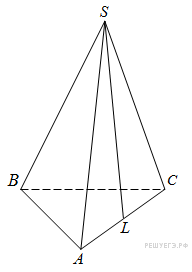В пра­виль­ной тре­уголь­ной пи­ра­ми­де SABC точка L — се­ре­ди­на ребра AC, S — вер­ши­на. Из­вест­но, что BC = 6, а SL = 5. Най­ди­те пло­щадь бо­ко­вой по­верх­но­сти пи­ра­ми­ды.

Ре­ше­ние.

От­ре­зок SL яв­ля­ет­ся ме­ди­а­ной пра­виль­но­го тре­уголь­ни­ка SAC, а зна­чит, и его вы­со­той. Бо­ко­вые грани пи­ра­ми­ды равны, по­это­му

Ответ: 45.

Ответ: 45

7. B 10 . 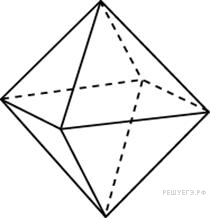Во сколь­ко раз уве­ли­чит­ся пло­щадь по­верх­но­сти ок­та­эд­ра, если все его ребра уве­ли­чить в 3 раза?

Ре­ше­ние.

При уве­ли­че­нии ребер в 3 раза пло­ща­ди тре­уголь­ни­ков, об­ра­зу­ю­щих грани ок­та­эд­ра, уве­ли­чат­ся в 9 раз, по­это­му сум­мар­ная пло­щадь по­верх­но­сти также уве­ли­чит­ся в 9 раз.

 

Ответ: 9.

Ответ: 9

8. B 10 . Най­ди­те угол пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да, для ко­то­ро­го =5, =4, =4. Дайте ответ в гра­ду­сах.

Ре­ше­ние.

грань яв­ля­ет­ся квад­ра­том со сто­ро­ной 4, а – диа­го­наль этой грани, зна­чит, угол равен

Ответ: 45.

Ответ: 45

9. B 10 . Вы­со­та ко­ну­са равна 6, а диа­метр ос­но­ва­ния – 16. Най­ди­те об­ра­зу­ю­щую ко­ну­са.

Ре­ше­ние.

об­ра­зу­ю­щая ко­ну­са по тео­ре­ме Пи­фа­го­ра равна

 

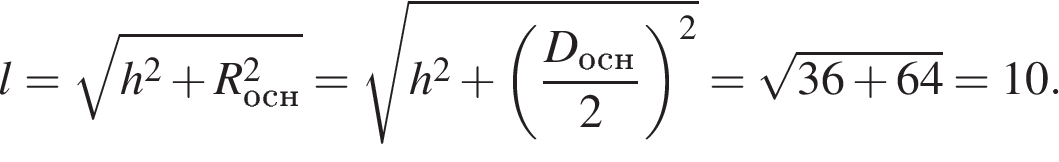
Ответ: 10.

Ответ: 10