
- •Вариант № 3701178
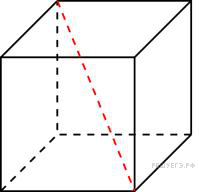
- •6. B 10 . Найдите объем многогранника, вершинами которого являются точки , , , прямоугольного параллелепипеда , у которого , , .
- •8.B 10 . Найдите угол многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
- •Вариант № 3701195
- •Вариант № 3701239
- •10. B 10 . Найдите объем многогранника, вершинами которого являются точки , , , прямоугольного параллелепипеда , у которого , , .
- •Вариант № 3704952
- •4. B 10 . Найдите угол многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
- •8. B 10 . Найдите объем многогранника, вершинами которого являются точки , , , прямоугольного параллелепипеда , у которого , , .
- •9. B 10 . Найдите объем многогранника, вершинами которого являются точки , , , прямоугольного параллелепипеда , у которого , , .
- •Вариант № 3706203
- •3. B 10 . Найдите объем многогранника, вершинами которого являются точки , , , прямоугольного параллелепипеда , у которого , , .
- •Вариант № 3706416
- •5. B 10 . В прямоугольном параллелепипеде известно, что Найдите длину ребра .
- •8. B 10 . Найдите объем многогранника, вершинами которого являются точки , , , прямоугольного параллелепипеда , у которого , , .
- •Вариант № 3706585
- •10. B 10 . Высота конуса равна 4, а длина образующей — 5. Найдите диаметр основания конуса.
- •Вариант № 3706631
- •Вариант № 3706686
- •8. B 10 . Высота конуса равна 4, а длина образующей — 5. Найдите диаметр основания конуса.
- •Вариант № 3706719
- •Вариант № 3706806
- •Вариант № 3706865
- •5.B 10 . Найдите угол многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
- •Вариант № 3706913
- •Вариант № 3706937
Вариант № 3701239
1.
B 10 .
 Объем
куба равен
Объем
куба равен
![]() .
Найдите его диагональ.
.
Найдите его диагональ.
Решение.
Если
ребро куба равно
![]() ,
то его объем и диагональ даются
формулами
,
то его объем и диагональ даются
формулами
![]() и
и
![]() Следовательно,
Следовательно,
![]()
Тогда диагональ равна 6.
Ответ: 6.
Ответ: 6
2.
B 10 .
 Найдите
квадрат расстояния между
вершинами C
и A1
прямоугольного
параллелепипеда, для
которого AB = 5,
AD = 4,
AA1=3.
Найдите
квадрат расстояния между
вершинами C
и A1
прямоугольного
параллелепипеда, для
которого AB = 5,
AD = 4,
AA1=3.
Решение.
Рассмотрим
прямоугольный треугольник
![]() в
котором
в
котором
![]() является
гипотенузой. По теореме
Пифагора
является
гипотенузой. По теореме
Пифагора
![]()
В
прямоугольнике
![]()
![]() – диагональ,
=
– диагональ,
=![]() .
Значит,
.
Значит,
![]()
![]()
Ответ: 50.
Ответ: 50
3. B 10 . Найдите угол прямоугольного параллелепипеда, для которого =5, =4, =4. Дайте ответ в градусах.
Решение.
грань является квадратом со стороной 4, а – диагональ этой грани, значит, угол равен
Ответ: 45.
Ответ: 45
4.
B 10 .
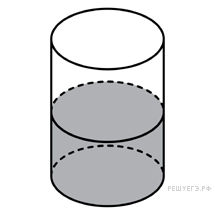 В
цилиндрический сосуд налили
2000
В
цилиндрический сосуд налили
2000
![]() воды.
Уровень воды при этом достигает
высоты 12 см. В жидкость полностью
погрузили деталь. При этом
уровень жидкости в сосуде
поднялся на 9 см. Чему равен объем
детали? Ответ выразите в
.
воды.
Уровень воды при этом достигает
высоты 12 см. В жидкость полностью
погрузили деталь. При этом
уровень жидкости в сосуде
поднялся на 9 см. Чему равен объем
детали? Ответ выразите в
.
Решение.
По закону Архимеда объем детали равен объему вытесненной ею жидкости. Объем вытесненной жидкости равен 9/12 исходного объема:
![]() .
.
Ответ: 1500.
Ответ: 1500
5. B 10 . Высота конуса равна 8, а диаметр основания — 30. Найдите образующую конуса.
Решение.
образующая конуса по теореме Пифагора равна
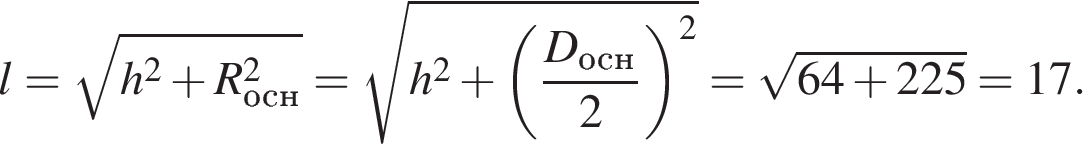
Ответ: 17.
Ответ: 17
6.
B 10 .
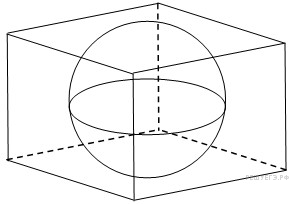 В
куб вписан шар радиуса 1.
Найдите объем куба.
В
куб вписан шар радиуса 1.
Найдите объем куба.
Решение.
Ребро куба равно диаметру вписанного в него шара, а объем куба равен кубу его ребра. Отсюда имеем:
![]() .
.
Ответ: 8.
Ответ: 8
7.
B 10 .
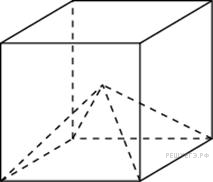 Объем
куба равен 12. Найдите объем
четырехугольной пирамиды,
основанием которой
является грань куба, а вершиной —
центр куба.
Объем
куба равен 12. Найдите объем
четырехугольной пирамиды,
основанием которой
является грань куба, а вершиной —
центр куба.
Решение.
Объем пирамиды равен
![]() .
.
Ответ: 2.
Примечание.
Куб состоит из 6 таких пирамид, объем каждой из них равен 2.
Ответ: 2
8.
B 10 .
В сосуде, имеющем форму
конуса, уровень жидкости
достигает
![]() высоты.
Объём жидкости равен 70 мл. Сколько
миллилитров жидкости
нужно долить, чтобы полностью
наполнить сосуд?
высоты.
Объём жидкости равен 70 мл. Сколько
миллилитров жидкости
нужно долить, чтобы полностью
наполнить сосуд?
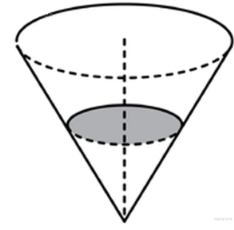
Решение.
Меньший конус подобен большему с коэффициентом 0,5. Объемы подобных тел относятся как куб коэффициента подобия. Поэтому объем большего конуса в 8 раз больше объема меньшего конуса, он равен 560 мл. Следовательно, необходимо долить 560 − 70 = 490 мл жидкости.
Ответ: 490.
Ответ: 490
9. B 10 . Найдите квадрат расстояния между вершинами и многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Решение.
рассмотрим прямоугольный треугольник По теореме Пифагора
Ответ: 11.
Ответ: 11
