Задание В10

Вариант № 3701178

1. B 10 . Вы­со­та ко­ну­са равна 4, а длина об­ра­зу­ю­щей — 5. Най­ди­те диа­метр ос­но­ва­ния ко­ну­са.

 

Ре­ше­ние.

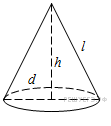Ра­ди­ус ос­но­ва­ния ко­ну­са, его вы­со­та и об­ра­зу­ю­щая свя­за­ны со­от­но­ше­ни­ем . В нашем слу­чае , по­это­му . Сле­до­ва­тель­но, диа­метр ос­но­ва­ния ко­ну­са равен 6.

Ответ: 6.

Ответ: 6

2. B 10 . 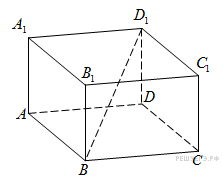В пря­мо­уголь­ном па­рал­ле­ле­пи­пе­де из­вест­но, что Най­ди­те длину ребра .

Ре­ше­ние.

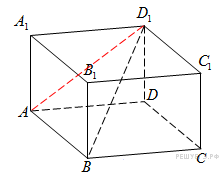По тео­ре­ме Пи­фа­го­ра

 

Тогда длина ребра равна

 

Ответ: 3.

Ответ: 3

3. B 10 . Най­ди­те угол пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да, для ко­то­ро­го =5, =4, =4. Дайте ответ в гра­ду­сах.

Ре­ше­ние.

грань яв­ля­ет­ся квад­ра­том со сто­ро­ной 4, а – диа­го­наль этой грани, зна­чит, угол равен

Ответ: 45.

Ответ: 45

4. B 10 . 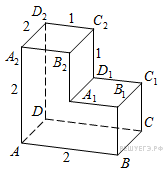Най­ди­те угол мно­го­гран­ни­ка, изоб­ра­жен­но­го на ри­сун­ке. Все дву­гран­ные углы мно­го­гран­ни­ка пря­мые. Ответ дайте в гра­ду­сах.

Ре­ше­ние.

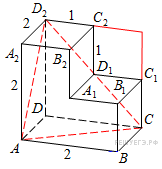Рас­смот­рим тре­уголь­ник где т. к. яв­ля­ют­ся диа­го­на­ля­ми рав­ных квад­ра­тов. Сле­до­ва­тель­но, тре­уголь­ник – рав­но­сто­рон­ний, по­это­му все его углы равны

Ответ: 60.

Ответ: 60

5. B 10 . 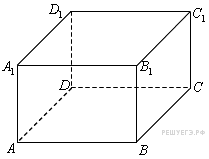Най­ди­те объем мно­го­гран­ни­ка, вер­ши­на­ми ко­то­ро­го яв­ля­ют­ся точки , , , пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да , у ко­то­ро­го , , .

 

Ре­ше­ние.

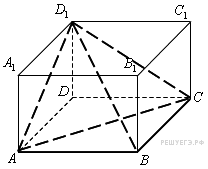Пло­щадь ос­но­ва­ния пи­ра­ми­ды в два раза мень­ше пло­ща­ди ос­но­ва­ния па­рел­ле­ле­пи­пе­да, а вы­со­та у них общая. По­это­му

 

 

 

Ответ: 8.

Ответ: 8

6. B 10 . Най­ди­те объем мно­го­гран­ни­ка, вер­ши­на­ми ко­то­ро­го яв­ля­ют­ся точки , , , пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да , у ко­то­ро­го , , .

 

Ре­ше­ние.

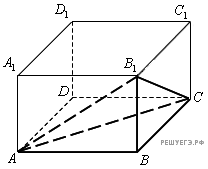Пло­щадь ос­но­ва­ния пи­ра­ми­ды в два раза мень­ше пло­ща­ди ос­но­ва­ния па­рел­ле­ле­пи­пе­да, а вы­со­та у них общая. По­это­му

 

 

 

Ответ: 6.

Ответ: 6

7.B 10 .

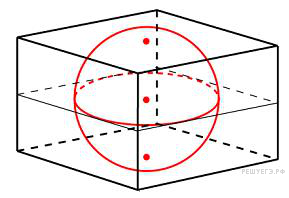
Объем пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да, опи­сан­но­го около сферы, равен 216. Най­ди­те ра­ди­ус сферы.

Ре­ше­ние.

Пря­мо­уголь­ный па­рал­ле­ле­пи­пед, опи­сан­ный во­круг сферы, яв­ля­ет­ся кубом. Тогда длина его ребра

 

.

Ра­ди­ус сферы равен по­ло­ви­не длины ребра .

Ответ: 3.

Ответ: 3

8.B 10 . Най­ди­те угол мно­го­гран­ни­ка, изоб­ра­жен­но­го на ри­сун­ке. Все дву­гран­ные углы мно­го­гран­ни­ка пря­мые. Ответ дайте в гра­ду­сах.

Ре­ше­ние.

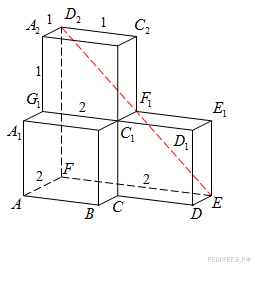
– диа­го­наль квад­ра­та со сто­ро­ной 2, зна­чит, тре­уголь­ник – пря­мо­уголь­ный и рав­но­бед­рен­ный, угол равен .

Ответ: 45.

Ответ: 45

9. B 10 . Шар впи­сан в ци­линдр. Пло­щадь по­верх­но­сти шара равна 111. Най­ди­те пло­щадь пол­ной по­верх­но­сти ци­лин­дра.

Ре­ше­ние.

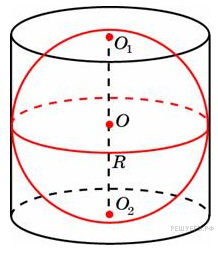
Вы­со­та ци­лин­дра равна диа­мет­ру шара, а ра­ди­ус ос­но­ва­ния ци­лин­дра равен ра­ди­у­су шара (см. рис.).

 

Пло­щадь ос­но­ва­ния ци­лин­дра:

 

Пло­щадь бо­ко­вой по­верх­но­сти ци­лин­дра:

 

Пло­щадь пол­ной по­верх­но­сти ци­лин­дра:

 

По­сколь­ку пло­щадь по­верх­но­сти шара да­ет­ся фор­му­лой имеем:

 

 

Ответ:166,5.

Ответ: 166,5

10. B 10 .

Вы­со­та ко­ну­са равна 4, а диа­метр ос­но­ва­ния — 6. Най­ди­те об­ра­зу­ю­щую ко­ну­са.