Вариант № 3658107

1. B 5 № 77152. 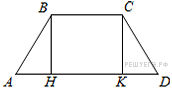Ос­но­ва­ния рав­но­бед­рен­ной тра­пе­ции равны 6 и 12. Синус остро­го угла тра­пе­ции равен 0,8. Най­ди­те бо­ко­вую сто­ро­ну.

Ре­ше­ние.

тре­уголь­ни­ки и равны ( ), зна­чит,

 

Ответ: 5.

Ответ: 5

2. B 5 № 245002.

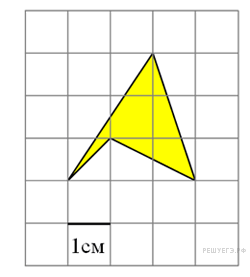Най­ди­те пло­щадь че­ты­рех­уголь­ни­ка, изоб­ра­жен­но­го на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см 1 см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах.

 

 

Ре­ше­ние.

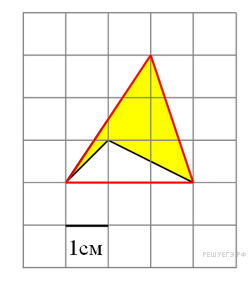Пло­щадь четырёхуголь­ни­ка равна раз­но­сти пло­ща­ди боль­шо­го тре­уголь­ни­ка и ма­лень­ко­го тре­уголь­ни­ка. По­это­му

 

.

Ответ: 3

3. B 5 № 27545. На клет­ча­той бу­ма­ге с клет­ка­ми раз­ме­ром 1 см 1 см изоб­ра­жен тре­уголь­ник (см. ри­су­нок). Най­ди­те его пло­щадь в квад­рат­ных сан­ти­мет­рах.

Ре­ше­ние.

Пло­щадь тре­уголь­ни­ка равна по­ло­ви­не про­из­ве­де­ния ос­но­ва­ния на вы­со­ту, про­ве­ден­ную к этому ос­но­ва­нию. По­это­му

см².

Ответ: 12.

Ответ: 12

4. B 5 № 27658. 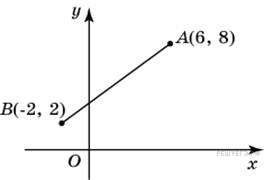Най­ди­те ор­ди­на­ту се­ре­ди­ны от­рез­ка, со­еди­ня­ю­ще­го точки A(6, 8) и B(-2, 2).

Ре­ше­ние.

Ко­ор­ди­на­ты точки, де­ля­щей от­ре­зок по­по­лам, счи­та­ют­ся по фор­му­ле:

 

, .

Ответ: 5.

Ответ: 5

5. B 5 № 27779. В тре­уголь­ни­ке угол равен , угол равен . , и – вы­со­ты, пе­ре­се­ка­ю­щи­е­ся в точке . Най­ди­те угол . Ответ дайте в гра­ду­сах.

Ре­ше­ние.

Угол между вы­со­та­ми равен углу между сто­ро­на­ми, к ко­то­рым они про­ве­де­ны: .

Ответ: 82.

Ответ: 82

6. B 5 № 27763. 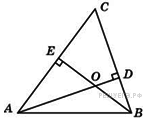Два угла тре­уголь­ни­ка равны и . Най­ди­те тупой угол, ко­то­рый об­ра­зу­ют вы­со­ты тре­уголь­ни­ка, вы­хо­дя­щие из вер­шин этих углов. Ответ дайте в гра­ду­сах.

Ре­ше­ние.

Cумма углов в вы­пук­лом четырёхуголь­ни­ке равна 360 гра­ду­сам, сле­до­ва­тель­но,

 

.

Ответ: 130.

Ответ: 130

7. B 5 № 27674. 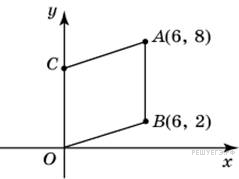Точки O(0; 0), A(6; 8), B(6; 2) и C яв­ля­ют­ся вер­ши­на­ми па­рал­ле­ло­грам­ма. Най­ди­те ор­ди­на­ту точки C.

Ре­ше­ние.

Так как у па­рал­ле­ло­грам­ма про­ти­во­по­лож­ные сто­ро­ны по­пар­но равны, то , . Из­вест­но, что имеет ко­ор­ди­на­ты , сле­до­ва­тель­но,

.

По­это­му .

 

Ответ: 6.

Ответ: 6

8. B 5 № 27699. 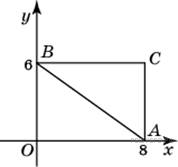Най­ди­те абс­цис­су цен­тра окруж­но­сти, опи­сан­ной около тре­уголь­ни­ка, вер­ши­ны ко­то­ро­го имеют ко­ор­ди­на­ты (8; 0), (0; 6), (8; 6).

Ре­ше­ние.

Тре­уголь­ник яв­ля­ет­ся пря­мо­уголь­ным. Центр окруж­но­сти, опи­сан­ной около пря­мо­уголь­но­го тре­уголь­ни­ка, сов­па­да­ет с се­ре­ди­ной ги­по­те­ну­зы. Тогда ко­ор­ди­на­ты цен­тра окруж­но­сти:

 

, .

Ответ: 4.

Ответ: 4

9. B 5 № 27794.

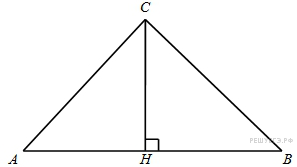В тре­уголь­ни­ке , , вы­со­та равна . Най­ди­те угол . Ответ дайте в гра­ду­сах.

Ре­ше­ние.

Вы­со­та в рав­но­бед­рен­ном тре­уголь­ни­ке яв­ля­ет­ся ме­ди­а­ной, по­это­му AH = 2. Рас­смот­рим тре­уголь­ник AHC, по тео­ре­ме Пи­фа­го­ра:

 

.

Угол АСН, ле­жа­щий про­тив ка­те­та, рав­но­го по­ло­ви­не ги­по­те­ну­зы, равен 30 По­сколь­ку ис­ко­мый угол ACB вдвое боль­ше, он равен 60

Ответ: 60.

Ответ: 60

10. B 5 № 27642. 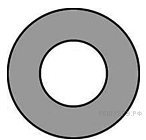Най­ди­те пло­щадь коль­ца, огра­ни­чен­но­го кон­цен­три­че­ски­ми окруж­но­стя­ми, ра­ди­у­сы ко­то­рых равны и .

Ре­ше­ние.

Пло­щадь круга опре­де­ля­ет­ся фор­му­лой S = πR². Пло­щадь коль­ца равна раз­но­сти пло­ща­дей пер­во­го и вто­ро­го круга. Тогда

 

, .

 

По­это­му пло­щадь коль­ца: S = S₁ − S₂ = 16 − 4 = 12.

 

Ответ: 12.

Ответ: 12