Вариант № 3658019

1. B 5 № 27682. Точки O(0; 0), B(8; 2), C(2; 6) и A яв­ля­ют­ся вер­ши­на­ми па­рал­ле­ло­грам­ма. Най­ди­те ор­ди­на­ту точки A.

Ре­ше­ние.

Пусть точка P яв­ля­ет­ся се­ре­ди­ной от­рез­ков OA и BC. Ко­ор­ди­на­ты точки P вы­чис­ля­ют­ся сле­ду­ю­щим об­ра­зом:

 

, ,

но с дру­гой сто­ро­ны,

, .

По­это­му ,

 

Ответ: 8.

Ответ: 8

2. B 5 № 27665. 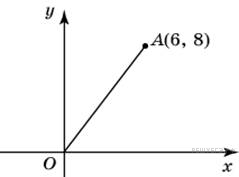Най­ди­те синус угла на­кло­на от­рез­ка, со­еди­ня­ю­ще­го точки O(0; 0) и A(6; 8), с осью абс­цисс.

Ре­ше­ние.

Если опу­стить из точки пер­пен­ди­ку­ляр на ось абс­цисс, то по­лу­чит­ся пря­мо­уголь­ный тре­уголь­ник. Длина

 

.

Тогда по­лу­ча­ет­ся, что

.

Ответ: 0,8.

Ответ: 0,8

3. B 5 № 27716. 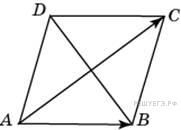Диа­го­на­ли ромба равны 12 и 16. Най­ди­те длину век­то­ра .

Ре­ше­ние.

Раз­ность век­то­ров равна век­то­ру . Диа­го­на­ли ромба пер­пен­ди­ку­ляр­ны и точ­кой пе­ре­се­че­ния де­лят­ся по­по­лам. Век­тор яв­ля­ет­ся ги­по­те­ну­зой в пря­мо­уголь­ном тре­уголь­ни­ке. По­это­му .

 

Ответ: 10.

Ответ: 10

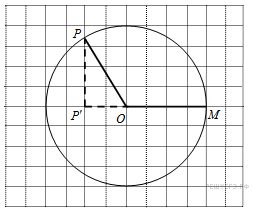
4. B 5 № 315133. На клет­ча­той бу­ма­ге изоб­ражён круг. Ка­ко­ва пло­щадь круга, если пло­щадь за­штри­хо­ван­но­го сек­то­ра равна 32?

Ре­ше­ние.

За­ме­тим, что Тогда по­это­му По­это­му пло­щадь сек­то­ра равна от пло­ща­ди круга. Сле­до­ва­тель­но, пло­щадь круга равна

 

Ответ:96.

Ответ: 96

5. B 5 № 27544. На клет­ча­той бу­ма­ге с клет­ка­ми раз­ме­ром 1 см 1 см изоб­ра­жен тре­уголь­ник (см. ри­су­нок). Най­ди­те его пло­щадь в квад­рат­ных сан­ти­мет­рах.

Ре­ше­ние.

Пло­щадь тре­уголь­ни­ка равна по­ло­ви­не про­из­ве­де­ния ос­но­ва­ния на вы­со­ту, про­ве­ден­ную к этому ос­но­ва­нию. По­это­му

см².

Ответ: 6.

Ответ: 6

6. B 5 № 245005. Най­ди­те пло­щадь че­ты­рех­уголь­ни­ка, изоб­ра­жен­но­го на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см 1 см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах.

Ре­ше­ние.

Пло­щадь четырёхуголь­ни­ка равна раз­но­сти пло­ща­ди тра­пе­ции, ма­лень­ко­го пря­мо­уголь­ни­ка и двух пря­мо­уголь­ных тре­уголь­ни­ков, ги­по­те­ну­зы ко­то­рых яв­ля­ют­ся сто­ро­на­ми ис­ход­но­го четырёхуголь­ни­ка. По­это­му

 

см².

 

 

При­ме­ча­ние.

Дан­ный четырёхуголь­ник можно раз­бить на пря­мо­уголь­ный тре­уголь­ник, с ка­те­та­ми 1 и 3, пря­мо­уголь­ную тра­пе­ию с ос­но­ва­ни­я­ми 3 и 1 и пря­мо­уголь­ный тре­уголь­ник с ка­те­та­ми 1 и 1. По­это­му его пло­щадь равна 4.

Ответ: 4

7. B 5 № 27737. Най­ди­те квад­рат длины век­то­ра  + .

Ре­ше­ние.

Ко­ор­ди­на­ты век­то­ра равны раз­но­сти ко­ор­ди­нат конца век­то­ра и его на­ча­ла. По­это­му век­тор имеет ко­ор­ди­на­ты , век­тор имеет ко­ор­ди­на­ты . Ко­ор­ди­на­ты суммы век­то­ров равны сумме со­от­вет­ству­ю­щих ко­ор­ди­нат. Тогда век­тор имеет ко­ор­ди­на­ты . Длина век­то­ра . По­это­му квад­рат длины век­то­ра равен .

 

Ответ: 200.

Ответ: 200

8. B 5 № 27848. Най­ди­те сред­нюю линию тра­пе­ции , если сто­ро­ны квад­рат­ных кле­ток равны 1.

Ре­ше­ние.

.

Ответ: 3.

Ответ: 3

9. B 5 № 27594. Сред­няя линия и вы­со­та тра­пе­ции равны со­от­вет­ствен­но 3 и 2. Най­ди­те пло­щадь тра­пе­ции.

Ре­ше­ние.

Пло­щадь тра­пе­ции равна про­из­ве­де­нию по­лу­сум­мы ос­но­ва­ний на вы­со­ту. Сред­няя линия тра­пе­ции равна по­лу­сум­ме ос­но­ва­ний. По­это­му

 

см².

Ответ: 6.

Ответ: 6

10. B 5 № 27803. 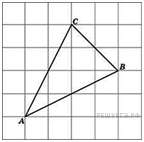Най­ди­те ме­ди­а­ну тре­уголь­ни­ка , про­ве­ден­ную из вер­ши­ны , если сто­ро­ны квад­рат­ных кле­ток равны 1.

Ре­ше­ние.

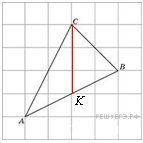ме­ди­а­на про­ве­ден­ная из вер­ши­ны , будет де­лить ос­но­ва­ние по­по­лам. По­стро­им от­ре­зок . Видно, что он равен 3.

Ответ: 3.

Ответ: 3