Вариант № 3657882

1. B 5 № 27858. Най­ди­те хорду, на ко­то­рую опи­ра­ет­ся угол , впи­сан­ный в окруж­ность ра­ди­у­са 3.

Ре­ше­ние.

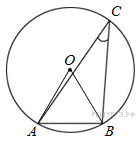
, зна­чит, , т. к. яв­ля­ет­ся цен­траль­ным углом, опи­ра­ю­щим­ся на ту же хорду. Со­от­вет­ствен­но, тре­уголь­ник – рав­но­сто­рон­ний, так как .

Ответ: 3.

Ответ: 3

2. B 5 № 27588. Пло­щадь пря­мо­уголь­но­го тре­уголь­ни­ка равна 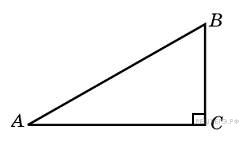16. Один из его ка­те­тов равен 4. Най­ди­те дру­гой катет.

Ре­ше­ние.

Пло­щадь пря­мо­уголь­но­го тре­уголь­ни­ка равна по­ло­ви­не про­из­ве­де­ния его ка­те­тов. Пусть не­из­вест­ный катет равен a. Тогда

см²,

от­ку­да a = 8 см.

Ответ: 8.

Ответ: 8

3. B 5 № 27604. Пе­ри­метр пря­мо­уголь­ни­ка равен 42, а пло­щадь 98. Най­ди­те боль­шую сто­ро­ну пря­мо­уголь­ни­ка.

Ре­ше­ние.

Пло­щадь пря­мо­уголь­ни­ка равна про­из­ве­де­нию его длины на ши­ри­ну. Пе­ри­метр пря­мо­уголь­ни­ка равен сумме длин всех сто­рон. Пусть одна из сто­рон пря­мо­уголь­ни­ка равна a, вто­рая равна b. Пло­щадь и пе­ри­метр пря­мо­уголь­ни­ка будут со­от­вет­ствен­но равны S = a   b = 98, P = 2   a + 2   b = 42. Решая од­но­вре­мен­но эти два урав­не­ния, по­лу­ча­ем, что a₁ = 7, a₂ = 14, b₁ = 14, b₂ = 7. По­это­му боль­шая сто­ро­на равна 14.

 

Ответ: 14.

Ответ: 14

4. B 5 № 315124. На клет­ча­той бу­ма­ге на­ри­со­ва­но два круга. Пло­щадь внут­рен­не­го круга равна 9. Най­ди­те пло­щадь за­штри­хо­ван­ной фи­гу­ры.

 

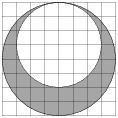
Ре­ше­ние.

Пло­ща­ди кру­гов от­но­сят­ся как квад­ра­ты их ра­ди­у­сов. По­сколь­ку ра­ди­ус боль­ше­го круга равен че­ты­рем тре­тьим ра­ди­у­са мень­ше­го круга, пло­щадь боль­ше­го круга со­став­ля­ет шест­на­дцать де­вя­тых пло­ща­ди мень­ше­го. Сле­до­ва­тель­но, она равна 16. Пло­щадь за­штри­хо­ван­ной фи­гу­ры равна раз­но­сти пло­ща­дей кру­гов: 16 − 9 = 7.

 

Ответ: 7.

Ответ: 7

5. B 5 № 27688. 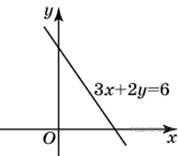Най­ди­те ор­ди­на­ту точки пе­ре­се­че­ния пря­мой, за­дан­ной урав­не­ни­ем 3x + 2y = 6, с осью Oy.

Ре­ше­ние.

Дан­ная пря­мая про­хо­дит через точки (0; y) и (x; 0). Тогда под­став­ляя эти точки в ис­ход­ное урав­не­ние пря­мой, по­лу­ча­ем x = 2, y = 3

 

Ответ: 3.

Ответ: 3

6. B 5 № 27691. Най­ди­те уг­ло­вой ко­эф­фи­ци­ент пря­мой, за­дан­ной урав­не­ни­ем 3x + 4y = 6.

Ре­ше­ние.

Общий вид урав­не­ния пря­мой y = kx + b. Тогда вы­ра­жая y из ис­ход­но­го урав­не­ния, по­лу­ча­ем, что y = −0,75x + 1,5. По­это­му k = −0,75.

 

Ответ: −0,75.

Ответ: -0,75

7. B 5 № 27758. 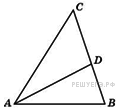В тре­уголь­ни­ке – бис­сек­три­са, угол равен , угол равен . Най­ди­те угол . Ответ дайте в гра­ду­сах.

Ре­ше­ние.

так как – бис­сек­три­са, она делит угол по­по­лам. Имеем

 

.

Ответ: 74.

 

Ответ: 74

8. B 5 № 27572. Най­ди­те пло­щадь тра­пе­ции, изоб­ра­жен­ной на ри­сун­ке.

Ре­ше­ние.

Пло­щадь тра­пе­ции равна про­из­ве­де­нию по­лу­сум­мы ос­но­ва­ний на вы­со­ту. По­это­му

 

см².

Ответ: 9.

Ответ: 9

9. B 5 № 27779. 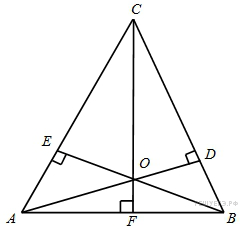В тре­уголь­ни­ке угол равен , угол равен . , и – вы­со­ты, пе­ре­се­ка­ю­щи­е­ся в точке . Най­ди­те угол . Ответ дайте в гра­ду­сах.

Ре­ше­ние.

Угол между вы­со­та­ми равен углу между сто­ро­на­ми, к ко­то­рым они про­ве­де­ны: .

Ответ: 82.

Ответ: 82

10. B 5 № 245005. 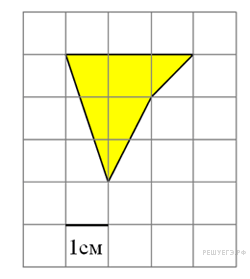Най­ди­те пло­щадь че­ты­рех­уголь­ни­ка, изоб­ра­жен­но­го на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см 1 см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах.

Ре­ше­ние.

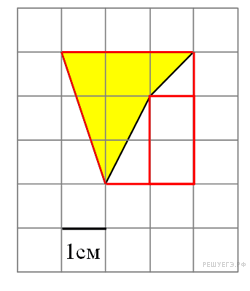Пло­щадь четырёхуголь­ни­ка равна раз­но­сти пло­ща­ди тра­пе­ции, ма­лень­ко­го пря­мо­уголь­ни­ка и двух пря­мо­уголь­ных тре­уголь­ни­ков, ги­по­те­ну­зы ко­то­рых яв­ля­ют­ся сто­ро­на­ми ис­ход­но­го четырёхуголь­ни­ка. По­это­му

 

см².

 

 

При­ме­ча­ние.

Дан­ный четырёхуголь­ник можно раз­бить на пря­мо­уголь­ный тре­уголь­ник, с ка­те­та­ми 1 и 3, пря­мо­уголь­ную тра­пе­ию с ос­но­ва­ни­я­ми 3 и 1 и пря­мо­уголь­ный тре­уголь­ник с ка­те­та­ми 1 и 1. По­это­му его пло­щадь равна 4.

Ответ: 4