Вариант № 3657850

1. B 5 № 27689. 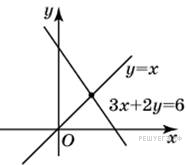Най­ди­те абс­цис­су точки пе­ре­се­че­ния пря­мых, за­дан­ных урав­не­ни­я­ми 3x + 2y = 6 и y = x.

Ре­ше­ние.

Решая си­сте­му этих двух урав­не­ний, по­лу­ча­ем, что y = x = 1,2.

 

Ответ: 1,2.

Ответ: 1,2

2. B 5 № 27941. 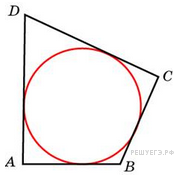В че­ты­рех­уголь­ник впи­са­на окруж­ность, , и . Най­ди­те чет­вер­тую сто­ро­ну че­ты­рех­уголь­ни­ка.

Ре­ше­ние.

В че­ты­рех­уголь­ник можно впи­сать окруж­ность тогда и толь­ко тогда, когда зна­чит,

 

Ответ: 14.

Ответ: 14

3. B 5 № 27628. 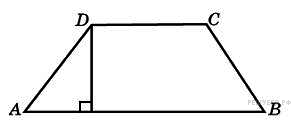Ос­но­ва­ние тра­пе­ции равно 13, вы­со­та равна 5, а пло­щадь равна 50. Най­ди­те вто­рое ос­но­ва­ние тра­пе­ции.

Ре­ше­ние.

 

.

Ответ: 7.

Ответ: 7

4. B 5 № 27845. Диа­го­на­ли че­ты­рех­уголь­ни­ка равны 4 и 5. Най­ди­те пе­ри­метр че­ты­рех­уголь­ни­ка, вер­ши­на­ми ко­то­ро­го яв­ля­ют­ся се­ре­ди­ны сто­рон дан­но­го че­ты­рех­уголь­ни­ка.

Ре­ше­ние.

Сто­ро­ны ис­ко­мо­го че­ты­рех­уголь­ни­ка равны сред­ним ли­ни­ям тре­уголь­ни­ков, об­ра­зу­е­мых диа­го­на­ля­ми и сто­ро­на­ми дан­но­го че­ты­рех­уголь­ни­ка. Таким об­ра­зом, сто­ро­ны ис­ко­мо­го че­ты­рех­уголь­ни­ка равны по­ло­ви­нам диа­го­на­лей. Со­от­вет­ствен­но,

 

.

Ответ: 9.

Ответ: 9

5. B 5 № 27811. 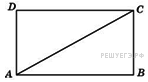Най­ди­те диа­го­наль пря­мо­уголь­ни­ка, две сто­ро­ны ко­то­ро­го равны и .

Ре­ше­ние.

по тео­ре­ме Пи­фа­го­ра диа­го­наль равна .

Ответ: 10.

Ответ: 10

6. B 5 № 27685.

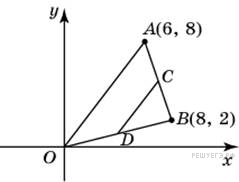Точки O(0; 0), A(6; 8), B(8; 2) яв­ля­ют­ся вер­ши­на­ми тре­уголь­ни­ка. Най­ди­те длину его сред­ней линии CD, па­рал­лель­ной OA.

Ре­ше­ние.

Точки C и D яв­ля­ют­ся се­ре­ди­на­ми сто­рон тре­уголь­ни­ка, тогда

 

, , , .

По­это­му

Ответ: 5.

При­ве­дем дру­гое ре­ше­ние.

За­ме­тим, что длина OA равна . Длина сред­ней линии вдвое мень­ше — она равна 5.

Ответ: 5

7. B 5 № 27737. 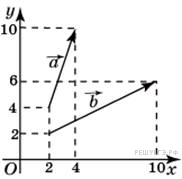Най­ди­те квад­рат длины век­то­ра  + .

Ре­ше­ние.

Ко­ор­ди­на­ты век­то­ра равны раз­но­сти ко­ор­ди­нат конца век­то­ра и его на­ча­ла. По­это­му век­тор имеет ко­ор­ди­на­ты , век­тор имеет ко­ор­ди­на­ты . Ко­ор­ди­на­ты суммы век­то­ров равны сумме со­от­вет­ству­ю­щих ко­ор­ди­нат. Тогда век­тор имеет ко­ор­ди­на­ты . Длина век­то­ра . По­это­му квад­рат длины век­то­ра равен .

 

Ответ: 200.

Ответ: 200

8. B 5 № 27719. Диа­го­на­ли ромба пе­ре­се­ка­ют­ся в точке и равны 12 и 16. Най­ди­те ска­ляр­ное про­из­ве­де­ние век­то­ров  и  .

Ре­ше­ние.

Ска­ляр­ное про­из­ве­де­ние двух век­то­ров равно про­из­ве­де­нию их длин на ко­си­нус угла между ними. Диа­го­на­ли в ромбе пер­пен­ди­ку­ляр­ны. Так как ко­си­нус пря­мо­го угла равен нулю, то и ска­ляр­ное про­из­ве­де­ние тоже равно нулю.

 

Ответ: 0.

Ответ: 0

9. B 5 № 27657.

Най­ди­те абс­цис­су се­ре­ди­ны от­рез­ка, со­еди­ня­ю­ще­го точки O(0, 0) и A(6, 8).

Ре­ше­ние.

Ко­ор­ди­на­ты точки, де­ля­щей от­ре­зок по­по­лам , счи­та­ют­ся по фор­му­ле:

 

, .

Ответ: 3.

Ответ: 3

10. B 5 № 27770. Ост­рые углы пря­мо­уголь­но­го тре­уголь­ни­ка равны и . Най­ди­те угол между вы­со­той и бис­сек­три­сой, про­ве­ден­ны­ми из вер­ши­ны пря­мо­го угла. Ответ дайте в гра­ду­сах.

Ре­ше­ние.

 

.

Ответ: 16.

Ответ: 16