Вариант № 3657799

1.B 5 № 27671. 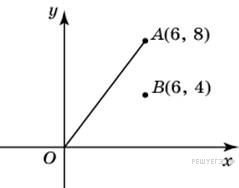Най­ди­те ор­ди­на­ту точки пе­ре­се­че­ния оси Oy и пря­мой, про­хо­дя­щей через точку B(6; 4) и па­рал­лель­ной пря­мой, про­хо­дя­щей через на­ча­ло ко­ор­ди­нат и точку A(6; 8).

Ре­ше­ние.

Урав­не­ние пря­мой имеет вид: , где  — уг­ло­вой ко­эф­фи­ци­ент. Тогда , под­став­ляя зна­че­ния абс­цисс и ор­ди­нат точек и , решая урав­не­ния од­но­вре­мен­но, по­лу­ча­ем:

 

.

Так как пря­мые па­рал­лель­ны, то

.

Те­перь под­став­ляя зна­че­ния и точку с ко­ор­ди­на­та­ми , зная еще, что ко­ор­ди­на­та вто­рой точки, при­над­ле­жа­щей пря­мой, , на­хо­дим .

 

Ответ: −4.

Ответ: -4

2.B 5 № 27584. Най­ди­те сто­ро­ну квад­ра­та, пло­щадь ко­то­ро­го равна пло­ща­ди пря­мо­уголь­ни­ка со сто­ро­на­ми 4 и 9. 

Ре­ше­ние.

Пло­щадь пря­мо­уголь­ни­ка равна про­из­ве­де­нию длины на ши­ри­ну . Пло­щадь квад­ра­та равна квад­ра­ту его сто­ро­ны. По­это­му сто­ро­на квад­ра­та, пло­щадь ко­то­ро­го равна 36, равна 6.

 

Ответ: 6.

Ответ: 6

3. B 5 № 27596. Най­ди­те пло­щадь круга, длина окруж­но­сти ко­то­ро­го равна .

Ре­ше­ние.

Пусть ра­ди­ус окруж­но­сти равен R, тогда пло­щадь круга опре­де­ля­ет­ся фор­му­лой S = πR², длина окруж­но­сти опре­де­ля­ет­ся фор­му­лой l = 2πR. По­это­му

 

, зна­чит,

Ответ: 0,25.

Ответ: 0,25

4.B 5 № 245001. 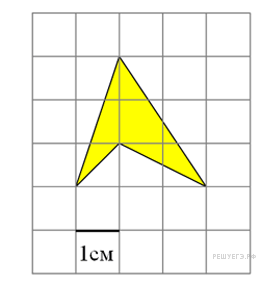Най­ди­те пло­щадь че­ты­рех­уголь­ни­ка, изоб­ра­жен­но­го на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см 1 см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах.

 

 

Ре­ше­ние.

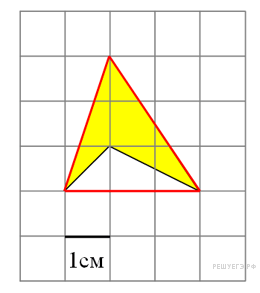Пло­щадь четырёхуголь­ни­ка равна раз­но­сти пло­ща­ди боль­шо­го тре­уголь­ни­ка и ма­лень­ко­го тре­уголь­ни­ка. По­это­му

 

.

Ответ: 3

5. B 5 № 27719. 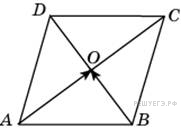Диа­го­на­ли ромба пе­ре­се­ка­ют­ся в точке и равны 12 и 16. Най­ди­те ска­ляр­ное про­из­ве­де­ние век­то­ров  и  .

Ре­ше­ние.

Ска­ляр­ное про­из­ве­де­ние двух век­то­ров равно про­из­ве­де­нию их длин на ко­си­нус угла между ними. Диа­го­на­ли в ромбе пер­пен­ди­ку­ляр­ны. Так как ко­си­нус пря­мо­го угла равен нулю, то и ска­ляр­ное про­из­ве­де­ние тоже равно нулю.

 

Ответ: 0.

Ответ: 0

6.B 5 № 27680. 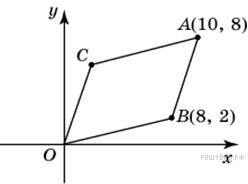Точки O(0; 0), A(10; 8), B(8; 2) и C яв­ля­ют­ся вер­ши­на­ми па­рал­ле­ло­грам­ма. Най­ди­те ор­ди­на­ту точки .

Ре­ше­ние.

Пусть точка P яв­ля­ет­ся се­ре­ди­ной от­рез­ков OA и BC. Ко­ор­ди­на­ты точки P вы­чис­ля­ют­ся сле­ду­ю­щим об­ра­зом:

 

, ,

но с дру­гой сто­ро­ны,

, .

По­это­му , .

 

Ответ: 6.

 

При­ве­дем дру­гое ре­ше­ние.

По­сколь­ку имеем: Сле­до­ва­тель­но, ор­ди­на­та точки С равна 6.

Ответ: 6

7. B 5 № 27848. 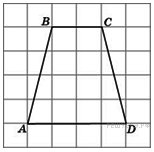Най­ди­те сред­нюю линию тра­пе­ции , если сто­ро­ны квад­рат­ных кле­ток равны 1.

Ре­ше­ние.

.

Ответ: 3.

Ответ: 3

8. B 5 № 27456. 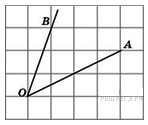Най­ди­те тан­генс угла .

Ре­ше­ние.

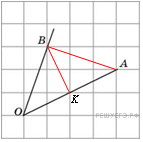До­стро­им угол до тре­уголь­ни­ка , . делит ос­но­ва­ние по­по­лам, зна­чит, – вы­со­та. Из ри­сун­ка на­хо­дим .

 

.

 

При­ме­ча­ние.

Можно за­ме­тить и до­ка­зать, что рав­но­бед­рен­ный тре­уголь­ник ABO яв­ля­ет­ся пря­мо­уголь­ным. Тогда углы AOB и OАB равны 45°, а их тан­ген­сы равны 1.

 

Ответ: 1.

Ответ: 1

9. B 5 № 27562. На клет­ча­той бу­ма­ге с клет­ка­ми раз­ме­ром 1 см 1 см изоб­ра­же­на фи­гу­ра (см. ри­су­нок). Най­ди­те ее пло­щадь в квад­рат­ных сан­ти­мет­рах. В от­ве­те за­пи­ши­те .

Ре­ше­ние.

Пло­щадь фи­гу­ры равна трем чет­вер­тым пло­ща­ди круга, ра­ди­ус ко­то­ро­го равен см. По­это­му

 

см².

Ответ: 12.

Ответ: 12

10. B 5 № 27681.

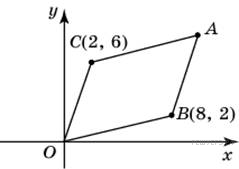Точки O(0; 0), B(8; 2), C(2; 6) и A яв­ля­ют­ся вер­ши­на­ми па­рал­ле­ло­грам­ма. Най­ди­те абс­цис­су точки A.

Ре­ше­ние.

Пусть точка P яв­ля­ет­ся се­ре­ди­ной от­рез­ков OA и BC. Ко­ор­ди­на­ты точки P вы­чис­ля­ют­ся сле­ду­ю­щим об­ра­зом:

 

, ,

но с дру­гой сто­ро­ны,

, .

По­это­му , .

 

Ответ: 10.

Ответ: 10