Вариант № 3658694

1. B 5 № 245006.

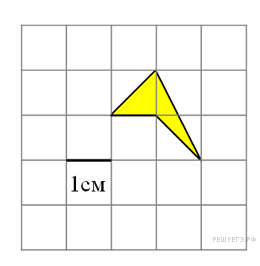Най­ди­те пло­щадь че­ты­рех­уголь­ни­ка, изоб­ра­жен­но­го на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см 1 см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах.

 

 

 

Ре­ше­ние.

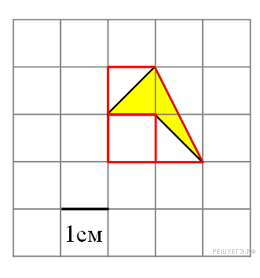Пло­щадь четырёхуголь­ни­ка равна раз­но­сти пло­ща­ди тра­пе­ции, ма­лень­ко­го пря­мо­уголь­ни­ка и двух пря­мо­уголь­ных тре­уголь­ни­ков, ги­по­те­ну­зы ко­то­рых яв­ля­ют­ся сто­ро­на­ми ис­ход­но­го четырёхуголь­ни­ка. По­это­му

 

.

 

 

При­ме­ча­ние.

Четырёхуголь­ник со­став­лен из двух тре­уголь­ни­ков, име­ю­щих общее ос­но­ва­ние, рав­ное длине квад­рат­ной клет­ки: пря­мо­уголь­но­го с ка­те­та­ми 1 и 1, и ту­по­уголь­но­го с ос­но­ва­ни­ем длины 1 и вы­со­той, про­ве­ден­ной к этому ос­но­ва­нию, также длины 1. По­это­му пло­щадь че­ты­рех­уголь­ни­ка равна 0,5 + 0,5 = 1.

Ответ: 1

2. B 5 № 27588

. Пло­щадь пря­мо­уголь­но­го тре­уголь­ни­ка равна 16. Один из его ка­те­тов равен 4. Най­ди­те дру­гой катет.

Ре­ше­ние.

Пло­щадь пря­мо­уголь­но­го тре­уголь­ни­ка равна по­ло­ви­не про­из­ве­де­ния его ка­те­тов. Пусть не­из­вест­ный катет равен a. Тогда

см²,

от­ку­да a = 8 см.

Ответ: 8.

Ответ: 8

3. B 5 № 319056. Пло­щадь па­рал­ле­ло­грам­ма равна 153. Най­ди­те пло­щадь па­рал­ле­ло­грам­ма , вер­ши­на­ми ко­то­ро­го яв­ля­ют­ся се­ре­ди­ны сто­рон дан­но­го па­рал­ле­ло­грам­ма.

Ре­ше­ние.

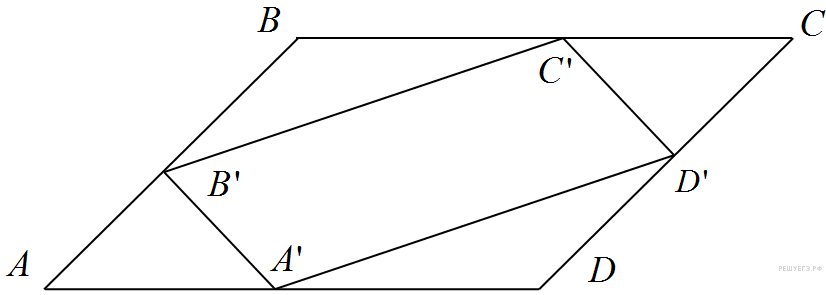
Че­ты­рех­уголь­ник, вер­ши­на­ми ко­то­ро­го яв­ля­ют­ся се­ре­ди­ны сто­рон про­из­воль­но­го че­ты­рех­уголь­ни­ка, яв­ля­ет­ся па­рал­ле­ло­грам­мом, пло­щадь ко­то­ро­го равна по­ло­ви­не пло­ща­ди ис­ход­но­го че­ты­рех­уголь­ни­ка (см. па­рал­ле­ло­грамм Ва­ри­ньо­на).

 

По­это­му его пло­щадь равна 76,5.

 

 

Ответ:76,5.

Ответ: 76,5

4. B 5 № 27948. 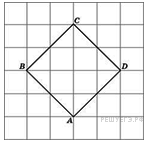Най­ди­те ра­ди­ус окруж­но­сти, впи­сан­ной в квад­рат , счи­тая сто­ро­ны квад­рат­ных кле­ток рав­ны­ми .

Ре­ше­ние.

ра­ди­ус окруж­но­сти, впи­сан­ной в квад­рат, равен по­ло­ви­не его сто­ро­ны.

 

Ответ: 2.

Ответ: 2

5. B 5 № 27716. Диа­го­на­ли ромба равны 12 и 16. Най­ди­те длину век­то­ра .

Ре­ше­ние.

Раз­ность век­то­ров равна век­то­ру . Диа­го­на­ли ромба пер­пен­ди­ку­ляр­ны и точ­кой пе­ре­се­че­ния де­лят­ся по­по­лам. Век­тор яв­ля­ет­ся ги­по­те­ну­зой в пря­мо­уголь­ном тре­уголь­ни­ке. По­это­му .

 

Ответ: 10.

Ответ: 10

6. B 5 № 55603.

Пло­щадь круга равна . Най­ди­те длину его окруж­но­сти.

Ре­ше­ние.

Пусть ра­ди­ус окруж­но­сти равен R, тогда пло­щадь круга опре­де­ля­ет­ся фор­му­лой S = πR², длина окруж­но­сти опре­де­ля­ет­ся фор­му­лой l = 2πR. По­это­му

 

, , зна­чит,

Ответ: 42.

Ответ: 42

7. B 5 № 244983. Най­ди­те пло­щадь ромба, изоб­ра­жен­но­го на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см 1 см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах.

 

 

Ре­ше­ние.

Пло­щадь четырёхуголь­ни­ка равна раз­но­сти пло­ща­ди боль­шо­го квад­ра­та, двух ма­лень­ких квад­ра­тов и четырёх пря­мо­уголь­ных тре­уголь­ни­ков, ги­по­те­ну­зы ко­то­рых яв­ля­ют­ся сто­ро­на­ми ис­ход­но­го тре­уголь­ни­ка. По­это­му

 

.

 

При­ме­ча­ние.

Наш четырёхуголь­ник — ромб, его пло­щадь равна по­ло­ви­не про­из­ве­де­ния диа­го­на­лей. По­это­му она равна 3.

Ответ: 3

8. B 5 № 27747. 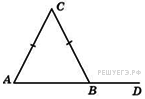В тре­уголь­ни­ке . Внеш­ний угол при вер­ши­не равен . Най­ди­те угол . Ответ дайте в гра­ду­сах.

Ре­ше­ние.

так как тре­уголь­ник рав­но­бед­рен­ный, то углы при его ос­но­ва­нии равны.

 

.

Ответ: 64.

Ответ: 64

9. B 5 № 27896. Ги­по­те­ну­за пря­мо­уголь­но­го тре­уголь­ни­ка равна 12. Най­ди­те ра­ди­ус опи­сан­ной окруж­но­сти этого тре­уголь­ни­ка.

Ре­ше­ние.

впи­сан­ный угол опи­ра­ю­щий­ся на диа­метр окруж­но­сти, яв­ля­ет­ся пря­мым, зна­чит, – диа­метр.

 

Ответ: 6.

Ответ: 6

10. B 5 № 27605.

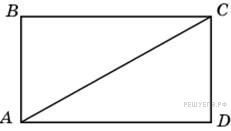Пе­ри­метр пря­мо­уголь­ни­ка равен 28, а диа­го­наль равна 10. Най­ди­те пло­щадь этого пря­мо­уголь­ни­ка.