Вариант № 3658576

1. B 5 № 27858. Най­ди­те хорду, на ко­то­рую опи­ра­ет­ся угол , впи­сан­ный в окруж­ность ра­ди­у­са 3.

Ре­ше­ние.

, зна­чит, , т. к. яв­ля­ет­ся цен­траль­ным углом, опи­ра­ю­щим­ся на ту же хорду. Со­от­вет­ствен­но, тре­уголь­ник – рав­но­сто­рон­ний, так как .

Ответ: 3.

Ответ: 3

2. B 5 № 27456. Най­ди­те тан­генс угла .

Ре­ше­ние.

До­стро­им угол до тре­уголь­ни­ка , . делит ос­но­ва­ние по­по­лам, зна­чит, – вы­со­та. Из ри­сун­ка на­хо­дим .

 

.

 

При­ме­ча­ние.

Можно за­ме­тить и до­ка­зать, что рав­но­бед­рен­ный тре­уголь­ник ABO яв­ля­ет­ся пря­мо­уголь­ным. Тогда углы AOB и OАB равны 45°, а их тан­ген­сы равны 1.

 

Ответ: 1.

Ответ: 1

3. B 5 № 27670. 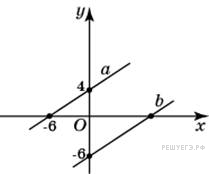Пря­мая a про­хо­дит через точки с ко­ор­ди­на­та­ми (0; 4) и (−6; 0). Пря­мая b про­хо­дит через точку с ко­ор­ди­на­та­ми (0; −6) и па­рал­лель­на пря­мой a. Най­ди­те абс­цис­су точки пе­ре­се­че­ния пря­мой b с осью O

Ре­ше­ние.

Пря­мые па­рал­лель­ны, по­это­му их уг­ло­вые ко­эф­фи­ци­ен­ты равны. Тогда , от­ку­да .

 

Ответ: 9.

Ответ: 9

4. B 5 № 27571.

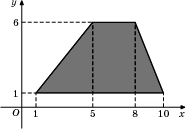Най­ди­те пло­щадь тра­пе­ции, вер­ши­ны ко­то­рой имеют ко­ор­ди­на­ты (1;1), (10;1), (8;6), (5;6).

Ре­ше­ние.

Пло­щадь тра­пе­ции равна про­из­ве­де­нию по­лу­сум­мы ос­но­ва­ний на вы­со­ту. По­это­му

 

см².

Ответ: 30.

Ответ: 30

5. B 5 № 27674.

Точки O(0; 0), A(6; 8), B(6; 2) и C яв­ля­ют­ся вер­ши­на­ми па­рал­ле­ло­грам­ма. Най­ди­те ор­ди­на­ту точки C.

Ре­ше­ние.

Так как у па­рал­ле­ло­грам­ма про­ти­во­по­лож­ные сто­ро­ны по­пар­но равны, то , . Из­вест­но, что имеет ко­ор­ди­на­ты , сле­до­ва­тель­но,

.

По­это­му .

 

Ответ: 6.

Ответ: 6

6. B 5 № 27726.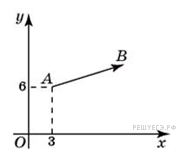

Век­тор  с на­ча­лом в точке (3; 6) имеет ко­ор­ди­на­ты (9; 3). Най­ди­те сумму ко­ор­ди­нат точки .

Ре­ше­ние.

Пусть ко­ор­ди­на­ты точки B равны x_B и y_B. x_B. Ко­ор­ди­на­ты век­то­ра равны раз­но­сти со­от­вет­ству­ю­щих ко­ор­ди­нат его конца и на­ча­ла. Сле­до­ва­тель­но, x_B − 3 = 9, y_B − 6 = 3. От­ку­да x_B = 12, y_B = 9. По­это­му сумма ко­ор­ди­нат точки B равна 21.

 

Ответ: 21.

Ответ: 21

7. B 5 № 27564. Най­ди­те пло­щадь тре­уголь­ни­ка, вер­ши­ны ко­то­ро­го имеют ко­ор­ди­на­ты (1;6), (9;6), (7;9).

Ре­ше­ние.

Пло­щадь тре­уголь­ни­ка равна по­ло­ви­не про­из­ве­де­ния ос­но­ва­ния на вы­со­ту, про­ве­ден­ную к этому ос­но­ва­нию. По­это­му

 

см².

Ответ: 12.

Ответ: 12

8. B 5 № 27925. Бо­ко­вая сто­ро­на рав­но­бед­рен­ной тра­пе­ции равна ее мень­ше­му ос­но­ва­нию, угол при ос­но­ва­нии равен 60°, боль­шее ос­но­ва­ние равно 12. Най­ди­те ра­ди­ус опи­сан­ной окруж­но­сти этой тра­пе­ции.

Ре­ше­ние.

Окруж­ность, опи­сан­ная во­круг тра­пе­ции, опи­са­на и во­круг тре­уголь­ни­ка . Это тре­уголь­ник рав­но­бед­рен­ный, угол при вер­ши­не равен 120°, углы при ос­но­ва­нии равны 30°. Най­дем его бо­ко­вую сто­ро­ну:

 

от­ку­да Тогда по тео­ре­ме си­ну­сов:

 

Ответ: 6.

При­ве­дем дру­гое ре­ше­ние (Р. А., СПб.).

 

Хорды AD, DC и CB равны, по­это­му равны и стя­ги­ва­е­мые ими дуги. Впи­сан­ный угол А равен 60°, он опи­ра­ет­ся на две из этих дуг и равен по­ло­ви­не их суммы. По­это­му каж­дая из дуг равна 60°, их сумма равна 180°, а хорда АВ яв­ля­ет­ся диа­мет­ром. От­сю­да по­лу­ча­ем, что ис­ко­мый ра­ди­ус равен 6.

Ответ: 6

9. B 5 № 244993. Най­ди­те пло­щадь че­ты­рех­уголь­ни­ка, изоб­ра­жен­но­го на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см 1 см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах

Ре­ше­ние.

Пло­щадь четырёхуголь­ни­ка равна раз­но­сти пло­ща­ди боль­шо­го квад­ра­та, двух ма­лень­ких пря­мо­уголь­ни­ков и четырёх пря­мо­уголь­ных тре­уголь­ни­ков, ги­по­те­ну­зы ко­то­рых яв­ля­ют­ся сто­ро­на­ми ис­ход­но­го четырёхуголь­ни­ка. По­это­му .

 

При­ме­ча­ние.

Пло­щадь четырёхуголь­ни­ка, диа­го­на­ли ко­то­ро­го пер­пе­н­ли­ку­ляр­ны, равна по­ло­ви­не про­из­ве­де­ния диа­го­на­лей. По­это­му ис­ко­мая пло­щадь равна 4.

Ответ: 4

10. B 5 № 245004.

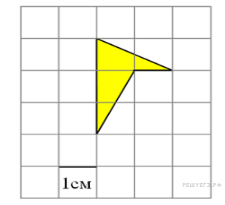Най­ди­те пло­щадь че­ты­рех­уголь­ни­ка, изоб­ра­жен­но­го на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см 1 см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах.