Вариант № 3658517
1.
B 5 № 27450.
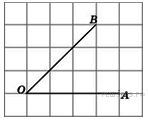Найдите
тангенс угла
.
Решение.
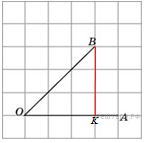проведем
высоту
из
точки
на
сторону
.
Тогда, принимая во внимание,
что
,
получим:
.
Ответ: 1.
Ответ: 1
2.
B 5 № 27552.
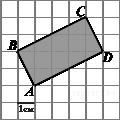Найдите
площадь прямоугольника
ABCD,
считая стороны квадратных
клеток равными 1.
Решение.
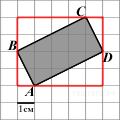Площадь
прямоугольника равна
разности площади
прямоугольника и четырех
прямоугольных треугольников,
гипотенузы которых
являются сторонами
исходного прямоугольника.
Поэтому
см2.
Ответ: 10.
Примечание
Для вычисления площади фигуры можно сложить площади треугольников BCD и BAD, имеющих общую сторону BD, длина которой равна 5, и равные проведенные к ней высоты длины 2.
Ответ: 10
3. B 5 № 27669.
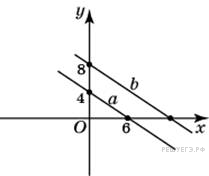Прямая
a
проходит через точки с
координатами (0; 4) и (6; 0).
Прямая b
проходит через точку с
координатами (0; 8) и
параллельна прямой a.
Найдите абсциссу точки
пересечения прямой b
с осью Ox
Решение.
Уравнение
прямой имеет вид
,
где
—
угловой коэффициент,
равный тангенсу угла наклона
прямой к оси абсцисс. Угловой
коэффициент прямой a
отрицателен и равен
.
Прямые а
и b
параллельны, поэтому их
угловые коэффициенты
равны. Следовательно,
уравнение прямой b
имеет вид
.
Точка
лежит
на прямой b,
поэтому
,
откуда
.
Тогда прямая b
задается уравнением
.
Осталось найти абсциссу точки
пересечения b
с осью абсцисс:
.
Приведем другое решение.
Параллельные прямые отсекают на сторонах угла пропорциональные отрезки. Прямая b на оси ординат отсекает отрезок вдвое больше, чем прямая a. Следовательно, на оси абсцисс она тоже отсекает отрезок вдвое большей длины. Поэтому искомая абсцисса равна 12.
Ответ: 12.
Ответ: 12
4. B 5 № 27544. На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
Решение.
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию. Поэтому
см2.
Ответ: 6.
Ответ: 6
5.
B 5 № 27937.
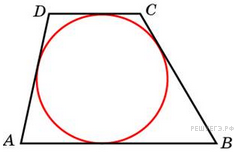Около
окружности описана трапеция,
периметр которой равен 40.
Найдите ее среднюю линию.
Решение.
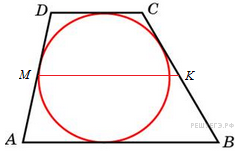В
выпуклый четырехугольник
можно вписать окружность тогда
и только тогда, когда
Ответ: 10.
Ответ: 10
6.
B 5 № 27938.
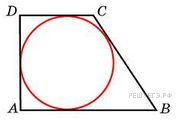Периметр
прямоугольной трапеции,
описанной около окружности,
равен 22, ее большая боковая
сторона равна 7. Найдите
радиус окружности.
Решение.
В четырехугольник можно вписать окружность тогда и только тогда, когда
Ответ: 2.
Ответ: 2
7.
B 5 № 27723.
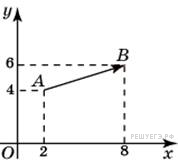Найдите
сумму координат вектора
.
Решение.
Координаты
вектора равны разности
координат конца вектора
и его начала. Вектор
имеет
координаты
.
Поэтому сумма координат
вектора
равна
8.
Ответ: 8.
Ответ: 8
8.
B 5 № 27936.
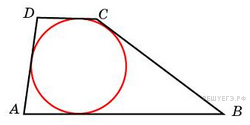Боковые
стороны трапеции, описанной
около окружности, равны 3 и 5.
Найдите среднюю линию трапеции.
Решение.
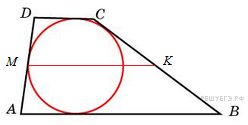
в выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда
Ответ: 4.
Ответ: 4
9. B 5 № 245003.
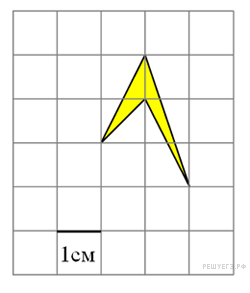Найдите
площадь четырехугольника,
изображенного на клетчатой
бумаге с размером клетки
1 см
1
см (см. рис.). Ответ дайте в квадратных
сантиметрах.
Решение.
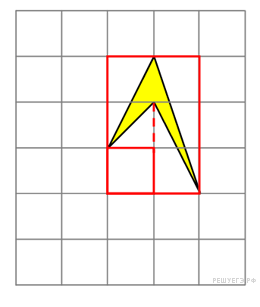Площадь
четырехугольника равна
разности площади большого
прямоугольника, четырёх
прямоугольных треугольников,
гипотенузы которых
являются сторонами
исходного четырехугольника
и площади маленького
квадрата. Поэтому
.
Примечание.
Заданный четырёхугольник можно рассматривать как два треугольника с общим основанием, равным длине квадратной клетки. Высоты этих треугольников равны 1, поэтому их площади 0,5, а сумма этих площадей равна 1.
Ответ: 1
10.
B 5 № 27697.
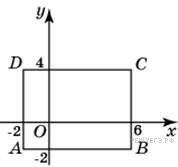Найдите
ординату центра окружности,
описанной около прямоугольника
ABCD,
вершины которого имеют
координаты соответственно
(−2; −2), (6; −2), (6; 4), (−2; 4).