Вариант № 3658424

1. B 5 № 27555. 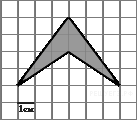На клет­ча­той бу­ма­ге с клет­ка­ми раз­ме­ром 1 см 1 см изоб­ра­же­на фи­гу­ра (см. ри­су­нок). Най­ди­те ее пло­щадь в квад­рат­ных сан­ти­мет­рах.

Ре­ше­ние.

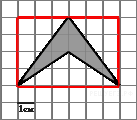Пло­щадь фи­гу­ры равна раз­но­сти пло­ща­ди пря­мо­уголь­ни­ка и трех тре­уголь­ни­ков. По­это­му

 

см².

Ответ: 6.

Ответ: 6

2. B 5 № 244989. Най­ди­те пло­щадь че­ты­рех­уголь­ни­ка, изоб­ра­жен­но­го на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см 1 см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах.

 

 

Ре­ше­ние.

Пло­щадь че­ты­рех­уголь­ни­ка равна раз­но­сти пло­ща­ди боль­шо­го пря­мо­уголь­но­го тре­уголь­ни­ка и ма­лень­ко­го пря­мо­уголь­но­го тре­уголь­ни­ка, ги­по­те­ну­за ко­то­ро­го яв­ля­ет­ся сто­ро­ной ис­ход­но­го че­ты­рех­уголь­ни­ка. По­это­му

.

Ответ: 2,5

3. B 5 № 27748.

В тре­уголь­ни­ке . Внеш­ний угол при вер­ши­не равен . Най­ди­те угол . Ответ дайте в гра­ду­сах.

Ре­ше­ние.

так как тре­уголь­ник рав­но­бед­рен­ный, то углы при его ос­но­ва­нии равны.

 

.

Ответ: 69.

 

Ответ: 69

4. B 5 № 27714. 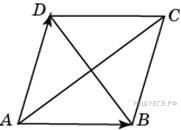Диа­го­на­ли изоб­ра­жен­но­го на ри­сун­ке ромба равны 12 и 16. Най­ди­те длину век­то­ра  + .

Ре­ше­ние.

Длина век­то­ра равна век­то­ру . Длина век­то­ра равна .

 

Ответ: 16.

Ответ: 16

5. B 5 № 27547. 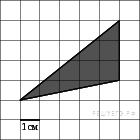На клет­ча­той бу­ма­ге с клет­ка­ми раз­ме­ром 1 см 1 см изоб­ра­жен тре­уголь­ник (см. ри­су­нок). Най­ди­те его пло­щадь в квад­рат­ных сан­ти­мет­рах.

Ре­ше­ние.

Пло­щадь тре­уголь­ни­ка равна по­ло­ви­не про­из­ве­де­ния ос­но­ва­ния на вы­со­ту, про­ве­ден­ную к этому ос­но­ва­нию или его про­дол­же­нию. Вы­бе­рем за ос­но­ва­ние вер­ти­каль­ную сто­ро­ну, дли­ной 3 клет­ки. Тогда про­ве­ден­ная к ней из левой ниж­ней вер­ши­ны тру­е­голь­ни­ка вы­со­та равна 5 клет­кам (см. рис.). По­это­му

см².

Ответ: 7,5.

Ответ: 7,5

6. B 5 № 319057. Пло­щадь па­рал­ле­ло­грам­ма равна 176. Точка – се­ре­ди­на сто­ро­ны . Най­ди­те пло­щадь тре­уголь­ни­ка .

Ре­ше­ние.

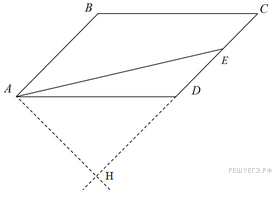
Пусть  − пер­пен­ди­ку­ляр, опу­щен­ный из точки на про­дол­же­ние сто­ро­ны Вы­ра­зим пло­щадь тре­уголь­ни­ка через пло­щадь па­рал­ле­ло­грам­ма

 

 

 

Ответ: 44.

Ответ: 44

7. B 5 № 27690. 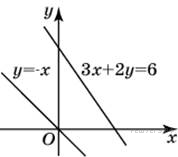Най­ди­те ор­ди­на­ту точки пе­ре­се­че­ния пря­мых, за­дан­ных урав­не­ни­я­ми 3x + 2y = 6 и y = −x.

Ре­ше­ние.

Решая сов­мест­но эти два урав­не­ния, по­лу­ча­ем, что x = 6, y = −6.

 

Ответ: −6.

Ответ: -6

8. B 5 № 27717. Диа­го­на­ли ромба пе­ре­се­ка­ют­ся в точке и равны 12 и 16. Най­ди­те длину век­то­ра  +  .

Ре­ше­ние.

Сумма век­то­ров  +  равна век­то­ру .  — ромб, его диа­го­на­ли пе­ре­се­ка­ют­ся под пря­мым углом, зна­чит,

.

Ответ: 10.

Ответ: 10

9. B 5 № 27564. 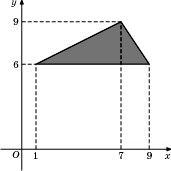Най­ди­те пло­щадь тре­уголь­ни­ка, вер­ши­ны ко­то­ро­го имеют ко­ор­ди­на­ты (1;6), (9;6), (7;9).

Ре­ше­ние.

Пло­щадь тре­уголь­ни­ка равна по­ло­ви­не про­из­ве­де­ния ос­но­ва­ния на вы­со­ту, про­ве­ден­ную к этому ос­но­ва­нию. По­это­му

 

см².

Ответ: 12.

Ответ: 12

10. B 5 № 27453. 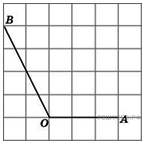Най­ди­те тан­генс угла .