
Вариант № 3658380
1.
B 5 № 27824.
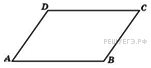 Две
стороны параллелограмма
относятся как
Две
стороны параллелограмма
относятся как
![]() ,
а периметр его равен 70. Найдите
большую сторону параллелограмма.
,
а периметр его равен 70. Найдите
большую сторону параллелограмма.
Решение.
Противоположные стороны параллелограмма попарно равны, значит,
![]() .
.
Зная,
что периметр параллелограмма
равен 70, находим:
![]() .
.
Ответ: 20.
Ответ: 20
2. B 5 № 27546.
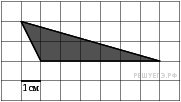 На
клетчатой бумаге с клетками
размером 1 см
1 см
изображен треугольник (см.
рисунок). Найдите его площадь
в квадратных сантиметрах.
На
клетчатой бумаге с клетками
размером 1 см
1 см
изображен треугольник (см.
рисунок). Найдите его площадь
в квадратных сантиметрах.
Решение.
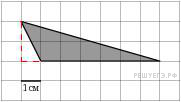 Площадь
треугольника равна половине
произведения основания
на высоту, проведенную к
этому основанию или его
продолжению. Поэтому
Площадь
треугольника равна половине
произведения основания
на высоту, проведенную к
этому основанию или его
продолжению. Поэтому
![]() см2.
см2.
Ответ: 6.
Ответ: 6
3.
B 5 № 27821.
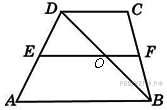 Основания
трапеции равны 4 и 10. Найдите
больший из отрезков, на которые
делит среднюю линию этой трапеции
одна из ее диагоналей.
Основания
трапеции равны 4 и 10. Найдите
больший из отрезков, на которые
делит среднюю линию этой трапеции
одна из ее диагоналей.
Решение.
больший
отрезок средней линии трапеции
является средней линией
треугольника
![]() ,
а значит, равен половине его
основания.
,
а значит, равен половине его
основания.
![]() .
.
Ответ: 5.
Ответ: 5
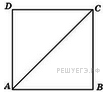
4.
B 5 № 27815.
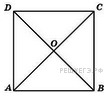 В
квадрате расстояние от
точки пересечения диагоналей
до одной из его сторон равно 7.
Найдите периметр этого
квадрата.
В
квадрате расстояние от
точки пересечения диагоналей
до одной из его сторон равно 7.
Найдите периметр этого
квадрата.
Решение.
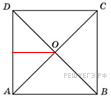 В
квадрате расстояние от
точки пересечения диагоналей
до стороны равно половине
стороны. Поэтому сторона
квадрата равна 14, а его периметр
56.
В
квадрате расстояние от
точки пересечения диагоналей
до стороны равно половине
стороны. Поэтому сторона
квадрата равна 14, а его периметр
56.
Ответ: 56.
Ответ: 56
5. B 5 № 27600.
Найдите площадь прямоугольника, если его периметр равен 18, и одна сторона на 3 больше другой.
Решение.
Площадь прямоугольника равна произведению его длины на ширину. Периметр прямоугольника равен сумме длин всех сторон. Пусть одна из сторон прямоугольника равна a, тогда вторая равна a+3. Периметр будет соответственно равен
P = 2 a + 2 (a + 3) = 18,
тогда одна из сторон будет равна 3, а другая 6. Поэтому
S = 3 6 = 18.
Ответ: 18.
Ответ: 18
6.
B 5 № 27549.
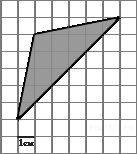 На
клетчатой бумаге с клетками
размером 1 см
1 см
изображен треугольник (см.
рисунок). Найдите его площадь
в квадратных сантиметрах.
На
клетчатой бумаге с клетками
размером 1 см
1 см
изображен треугольник (см.
рисунок). Найдите его площадь
в квадратных сантиметрах.
Решение.
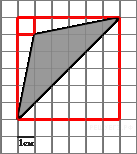 Площадь
треугольника равна разности
площади большого квадрата,
маленького квадрата и
трех прямоугольных треугольников,
гипотенузы которых
являются сторонами
исходного треугольника.
Поэтому
Площадь
треугольника равна разности
площади большого квадрата,
маленького квадрата и
трех прямоугольных треугольников,
гипотенузы которых
являются сторонами
исходного треугольника.
Поэтому
![]() см2.
см2.
Ответ: 12.
Ответ: 12
7.
B 5 № 27814.
 Найдите
сторону квадрата, диагональ
которого равна
Найдите
сторону квадрата, диагональ
которого равна
![]() .
.
Решение.
По
теореме Пифагора
![]() ,
значит,
,
значит,
![]() .
.
Ответ: 2.
Ответ: 2
8. B 5 № 27586.
Найдите площадь ромба, если его стороны равны 1, а один из углов равен 150°
Решение.
Площадь ромба равна произведению квадрата его стороны и синуса его угла. Поэтому
см2.
Ответ: 0,5.
Ответ: 0,5
9. B 5 № 27656.
Найдите ординату середины отрезка, соединяющего точки O (0; 0) и A (6; 8).
Решение.
Координаты точки, делящей отрезок пополам , считаются по формуле:
,
Ответ: 4.
Ответ: 4
10.
B 5 № 244991.
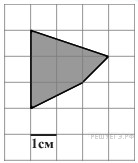 Найдите
площадь четырехугольника,
изображенного на клетчатой
бумаге с размером клетки
1 см
1
см (см. рис.). Ответ дайте в квадратных
сантиметрах.
Найдите
площадь четырехугольника,
изображенного на клетчатой
бумаге с размером клетки
1 см
1
см (см. рис.). Ответ дайте в квадратных
сантиметрах.
Решение.
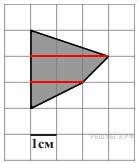 Площадь
четырехугольника равна
сумме площадей двух прямоугольных
треугольников и площади
трапеции. Поэтому
Площадь
четырехугольника равна
сумме площадей двух прямоугольных
треугольников и площади
трапеции. Поэтому
![]() .
.
Ответ: 5
Решение.
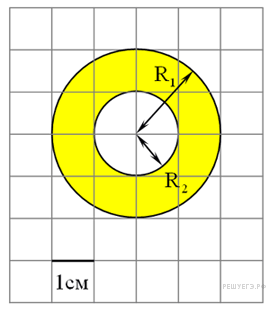 Площадь
кольца равна разности площади
большого и малого кругов.
Радиус большого круга равен
2, а малого — 1, откуда
Площадь
кольца равна разности площади
большого и малого кругов.
Радиус большого круга равен
2, а малого — 1, откуда
![]() .
.
Поэтому
![]() .
.
Ответ: 3
Решение.
так
как
![]() ,
то
,
то
![]() .
Тогда
.
Тогда
![]() ,
,
откуда,
![]() .
.
Ответ: 6.
Ответ: 6
