2.5. Проверка значимости коэффициентов регрессии

Напомним вид уравнения множественной линейной регрессии:

(1)

В программе «Регрессия» коэффициенты регрессии приведены в строке «Коэффициенты». Строка «Y-пересечение» - свободный член ; в других строка ниже: («Переменная Х1»); («Переменная Х2»). и т.д. Отметим, что на рис.2 приведен пример расчета парной регрессии , которая является частным случаем множественной.

Возможна ситуация, когда часть вычисленных коэффициентов регрессии не обладает необходимой степенью значимости. В этом случае значения рассматриваемых коэффициентов будут меньше величины их стандартной ошибки.

Поэтому наряду с проверкой адекватности полученного уравнения регрессии в целом (по значимости коэффициента детерминации ) необходимо выполнить проверку значимости каждого коэффициента регрессии.

Проверку значимости коэффициентов регрессии выполняют с помощью -критерия Стьюдента:

, (2)

где - значение рассматриваемого коэффициента регрессии; ;

- стандартная ошибка (погрешность) коэффициента ;

- расчетное значение коэффициента Стьюдента.

Формула для определения громоздкая и ее приводить не будем.

Коэффициент регрессии считается значимым при выполнении условия:

(3)

где - табличное значение коэффициента Стьюдента, выбираемое в зависимости от уровня значимости (обычно ) и степени свободы

. (4)

Здесь - количество факторов ; - число экспериментальных данных. В Excel для определения используется статистическая функция:

=СТЬДРАСПОБР( ; ).

В программе «Регрессия» значения приведены в столбце «Стандартная ошибка»; значения - в столбце « -статистика». Вместо условия (3) в данной программе вычисляются значения уровней значимости , соответствующие расчетным значениям . Они приведены в столбце «Р-значения». Для определения используется функция:

=СТЬЮДРАСП( ).

Если выполняется условие

, (5)

то коэффициент считается значимым. Здесь - заданный уровень значимости (обычно ).

Зная значения можно найти границы доверительных интервалов для коэффициентов регрессии:

;

(6)

.

В программе «Регрессия» приведены в столбце «Нижние 95%»; - «Верхние 95%».

Если незначимым окажется свободный член , то для пересчета уравнения регрессии без этого коэффициента в диалоговом окне «Регрессия» следует активировать флажок «Константы - ноль». В случае, если незначимым является коэффициент при факторном признаке , то следует исключить этот признак при задании уравнения регрессии.

Пример 1: получим уравнение множественной регрессии для зависимости функции от двух факторов, т.е. . Линейное уравнение имеет следующий вид: .

Воспользуемся данными из таблицы п. 2.1. В этой табл.: - уровень преступности ( ); - уровень образования ( ); - уровень безработицы ( ).

Результаты расчетов по программе «Регрессия» приведены на рис. 3.

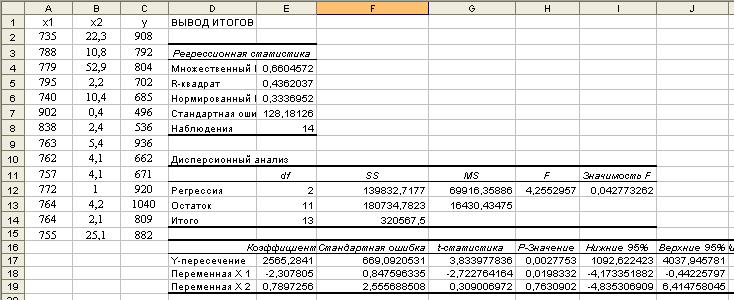
Рис. 3. Лист Excel с результатами работы программы «Регрессия»

(множественная регрессия)

Видно, что в целом уравнение значимо, но коэффициент при переменной не значим и его следует исключить из анализа (т.е. при обращении к программе не указывать массив ). Получив уравнение увидим, что в целом качество этого нового уравнения регрессии повысится (получим большее значение «F» и, следовательно, меньшую величину «Значимость F»).

Пример 2: по данным таблицы получить уравнение . Убедится, что не значим коэффициент . Исключить его, т.е. получить уравнение вида: . Выполнить самостоятельно.

Номер предприятия	Прибыль, млн. руб.	Величина оборотных средств, млн. руб.	Стоимость основных фондов, млн. руб.
1	188	129	510
2	78	64	190
3	93	69	240
4	152	87	470
5	55	47	110
6	161	102	420