2.3. Множественная линейная регрессия

Если исследуется связь между функцией отклика и двумя ( ), тремя ( ) или более факторами, то регрессия называется множественной. Параметр может также называться зависимой переменной, а - независимыми переменными.

Уравнение линейной множественной регрессии имеет вид:

, (1)

где - расчетное значение функции отклика, полученное путем подстановки соответствующих значений факторов в уравнение регрессии; - значения факторов; - коэффициенты регрессии.

Значения определяются с помощью МНК. Коэффициенты минимизируют сумму квадратов отклонений экспериментальных значений функции отклика от теоретических , полученных расчетом по выбранному уравнению регрессии:

. (2)

Рассматривая в качестве функции параметров , вычислим частные производные и приравняем их нулю

; ;…; . (3)

В результате получим систему нормальных уравнений с неизвестными (параметрами ):

(4)

Система (4) является линейной относительно неизвестных . Решается одним из известных способов. Например, методом обратной матрицы.

2.4. Проверка значимости (адекватности) уравнения регрессии в целом

После расчета коэффициентов регрессии необходимо оценить статистическую значимость (адекватность) полученного уравнения регрессии. Т.е. количественно оценить качество описания уравнением опытных данных.

Сначала рассчитаем суммы квадратов отклонения :

а) - сумма квадратов отклонений эмпирических данных от среднего:

. (1)

характеризует общую изменчивость , т.е. влияние как основных, так и остаточных факторов. Основные факторы – переменные , входящие в уравнение регрессии.

б) - сумма квадратов отклонений расчетных данных (по уравнению регрессии) от среднего:

. (2)

Данная величина характеризует факторную изменчивость, т.е. влияние на основных факторов .

в) - сумма квадратов отклонений эмпирических данных от расчетных:

. (3)

Данная величина характеризует остаточную изменчивость, отражающую влияние остаточных факторов на .

П ричем

;

(4)

.

В программе «Регрессия» в таблице «Дисперсионный анализ» суммы квадратов размещены в строках:

« » - заголовок столбца;

«Регрессия» → (факторная изменчивость);

«Остаток» → (остаточная изменчивость);

«Итого» → (общая изменчивость).

С указанными выше суммами квадратов (или изменчивостями) связаны следующие степени свободы:

для → степень свободы (число факторов );

для → степень свободы ;

для → степень свободы .

П ричем

;

(5)

.

В программе «Регрессия» степени свободы записаны в столбце « » и строках: «Регрессия» → ; «Остаток» → ; «Итого» → .

Отношение факторной изменчивости к общей называется коэффициентом детерминации:

. (6)

В программе «Регрессия» записан в строке « -квадрат» (таблица «Регрессионная статистика»).

Если , то функция отклика не зависит от факторов . Если , то изменчивость обусловлена влиянием только факторов .Все экспериментальные точки лежат на одной линии.

При вероятностной (стохастической связи) . При значениях

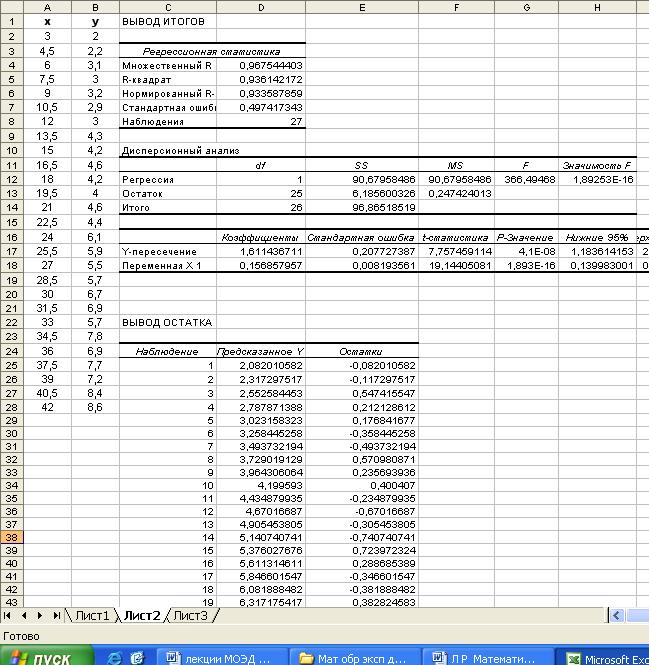
Рис. 2. Лист Excel с результатами работы программы «Регрессия»

(парная регрессия)

считается, что вариация функции отклика обусловлена в основном влиянием включенных в регрессионную модель факторов .

Коэффициент множественной корреляции . При зависимости от одного фактора . В программе - «Множественный ».

В большинстве случаев уравнение регрессии строят на основе выборочных данных. Поэтому необходимо оценить адекватность полученного уравнения генеральным данным. Для этого проводится проверка статистической значимости коэффициента детерминации по критерию Фишера:

, (7)

где - расчетное значение критерия Фишера;

- факторная дисперсия;

- остаточная дисперсия;

; (8)

. (9)

В программе «Регрессия» в таблице «Дисперсионный анализ» дисперсии находятся в столбце « » в строках:

→ «Регрессия»;

→ «Остаток»;

расчетное значение коэффициента Фишера – в столбце « ».

Коэффициент детерминации считается значимым при выполнении условия:

(10)

где - табличное значение коэффициента Фишера; его можно определить с использованием стандартной функции FРАСПОБР.

В программе «Регрессия» вместо проверки условия (10) заложен другой подход. В столбце «Значимость » приводится значение уровня значимости, соответствующее вычисленному значению . Обозначим его . Значение в программе определяется с использованием функции

.

Если выполняется условие

, (11)

то и в целом уравнение регрессии считается значимым. Здесь - заданный уровень значимости; обычно .

В программе в таблице «Регрессионная статистика» приводится значение «Стандартная ошибка». Это среднеквадратичное отклонение:

(12)

Чем меньше , тем лучше уравнение регрессии описывает опытные данные.