3. Силовой расчет механизма

Задачи силового расчета: определение реакций в кинематических парах; уравновешивающей силы (Р_ур) или уравновешивающего момента (М_ур).

Расчет выполнен двумя методами - методом планов и методом рычага Жуковского.

3.1. Силовой расчет механизма методом планов

Метод планов базируется на принципах механики - принципе Даламбера и принципе заменяемости связей.

Расчет проводят, начиная с наиболее удаленной от исходного механизма структурной группы, и заканчивают расчетом исходного механизма.

Исходными данными для расчета являются: кинематическая схема; все кинематические размеры; массы звеньев m₁, m₂, m₃; положения центров масс S₁ и S₂ кривошипа и шатуна; данные кинематического расчета; диаграмма силы полезного сопротивления и ее максимальное значение Р.

3.1.1. Силовой расчет структурной группы

Кинетостатический расчет механизма выполнен для двух его положений (5 и 4).

Расчет начинается с определения внешних сил, действующих на звенья, входящие в структурную группу. К ним относятся силы тяжести G₂ и G₃, силы инерции, сила полезного сопротивления Р_пс.

Сила тяжести i-го звена (i=2,3) вычисляется по формуле

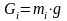, где m_i - масса i-го звена; g - ускорение свободного падения, g = 9,8 м/с².

Сила тяжести шатуна:

.

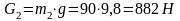Сила тяжести ползуна:

.

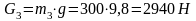В соответствии с принципом Даламбера вычисляем силы инерции ползуна и шатуна. Для расчета сил инерции шатуна заменим его двумя точечными массами m_A2 и m_B2, расположенными в центрах шарниров А и В.

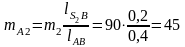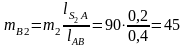кг; кг.

Силы инерции замещающих масс:

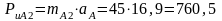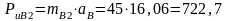Н;

Н.

Сила инерции ползуна:

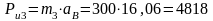Н.

Для определения силы полезного сопротивления P_ncj в рассматриваемом j-м положении механизма над разметкой строится диаграмма силы полезного сопротивления (рис. 7). Ось абсцисс диаграммы параллельна направляющей t-t ползуна, а начало ее системы координат соответствует началу рабочего хода механизма, т.е. точке В₀ на разметке. Ось ординат направлена перпендикулярно t-t.

Масштабный коэффициент μ_р диаграммы P_пс(S_B) вычисляется по формуле

μ_р = Р(Н)/Р(мм), где 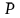- длина отрезка, которым максимальное значение силы Р изображается на диаграмме.

μ_р = 600000/60 = 10000 Н/мм.

Для определения значения Р_пс5 силы полезного сопротивления в расчетном 5-м положении механизма из точки В₅ на траектории движения ползуна восстанавливаем перпендикуляр к оси t-t до пересечения с графиком P_пс(S_B). Измеряем ординату 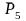в миллиметрах. Величина силы полезного сопротивления вычисляется по формуле

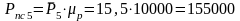Н.

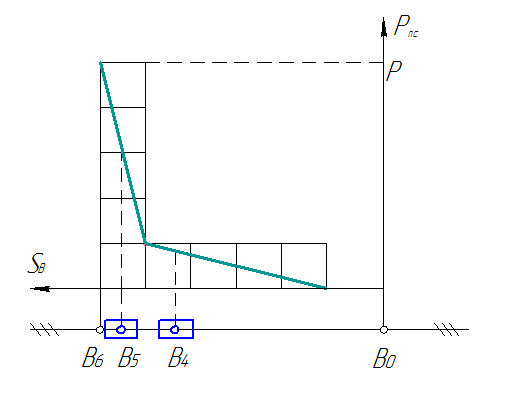
Рис. 7.

На рис. 8 приведена схема нагружения структурной группы в 5-м положении механизма.

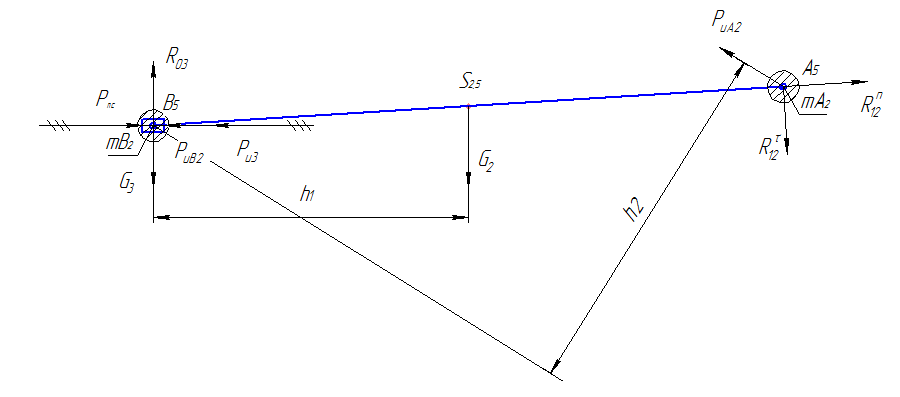
Рис. 8. Схема нагружения структурной группы

Под действием указанной системы сил структурная группа находится в равновесии. В равновесии находится и каждое звено этой группы. Реакция 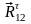определяется по условию равновесия системы сил, действующих на шатун:

.

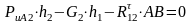Плечи сил измеряются в мм на схеме нагружения.

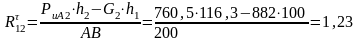Н.

Знак реакции свидетельствует о том, что ее направление соответствует указанному на схеме нагружения.

Условие равновесия системы сил, действующих на структурную группу:

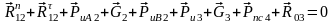. (3.1)

Графическое решение уравнения (3.1) приведено на рис. 9.

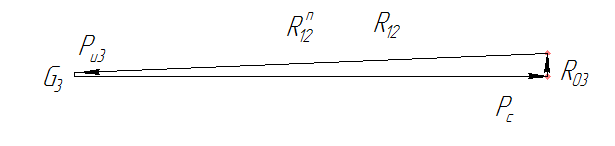
Рис. 9. План сил

Масштабный коэффициент плана сил:

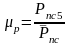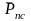, где - длина отрезка, которым сила полезного сопротивления изображается на плане сил.

μ_р = 155000/77,5 = 2 кН/мм.

Точку приложения реакции 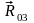определяем по условию равновесия системы сил, действующих на ползун.

.

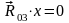Реакция не равна нулю, следовательно, х=0. Таким образом, линия действия реакции проходит через геометрический центр шарнира В.

Расчет модулей искомых реакций: