3.1 Классификация нечетких моделей
Нечеткие модели в зависимости от типа входных и выходных параметров можно разделить следующим образом (Рис. 3).
Продукционное правило в
форме условного высказывания
«если А, то В»
A – лингвистическое
высказывание, B – функция, f
– четкая функция
А, В – лингвистические
высказывания, f
– нечеткая функция
А, В – лингвистические
высказывания, f
– четкая функция
Модель Такаги-Суджено
Нечеткая
реляционная
модель
Нечеткая
лингвистическая
модель
Рис. 3 – классификация нечетких моделей
Лингвистическая нечеткая модель имеет вид
где
,
– входная и выходная лингвистические
переменные;
–лингвистические термы (им соответствуют
нечеткие переменные с определенными
функциями принадлежности).
Каждое
правило можно рассматривать как нечеткое
отношение
которое вычисляется на основе нечеткой
импликации, формализующей причинную
связь между посылкой и заключением в
виде
.
Существуют различные представления
импликации. В самом простом и
распространённом случае
тогда нечеткое отношение , соответствующее совокупности продукционных правил, определяется следующим образом:
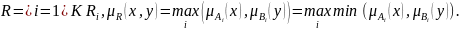
Нечеткая реляционная модель может быть рассмотрена как расширение лингвистической модели, в которой отображение между входными и выходными нечеткими множествами представляется нечеткими отношениями. Введем
и
– множество лингвистических термов,
определенных для переменных посылок и
переменных заключений соответственно.
База правил может быть представлена
как нечеткое отношение между
лингвистическими термами посылок и
заключений
В этой модели каждое правило содержит
все возможные термы следствий, причем
со своим весовым коэффициентом, заданным
соответствующим элементом нечеткого
отношения. С помощью этого веса можно
легко настраивать модель.
Модель Takagi – Sugeno (TS-модель) можно рассматривать как комбинацию лингвистической и регрессионной модели. Она задается в следующем виде:
В
данной модели посылка представляет
собой нечеткое высказывание, а заключение
– четкую функцию. Функции
обычно имеют одинаковую структуру,
только параметры для каждого правила
различны.
3.1.1 Структура модели
Мы
применяем нечеткие правила классификации,
каждое из которых описывает один из
классов
в наборе данных. Априорное правило
является нечетким описанием в n-мерном
пространстве свойств и последовательность
правил является свежей (ненечеткой)
меткой класса из множества
:
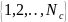Здесь
обозначает число свойств,
– входной вектор,
– вывод i-го
правила и
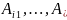предшествующие нечеткие множества.
Степень активации i-го
правила вычисляется как:
Выход классификатора затем определяется правилом, которое имеет наивысшую степень активации:
В дальнейшем мы предполагаем, что число классов соответствует числу правил, т.е. M= . Степень уверенности в решении дана нормализованной степенью запуска правила:
3.1.2 Управляемая данными инициализация
Из
К доступных входящих-выходящих пар
данных
мы строим n-мерный
шаблон матрицы
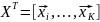и соответствующий вектор-метку
.
Нечеткие антецеденты
в начальной базе правил теперь определены
алгоритмом с тремя шагами.
Шаг
1:
М функций принадлежности многих
переменных определяются в пространстве
функций продукта. Каждая описывает
область, где система может быть приближена
единственным нечетким правилом. Это
разбиение может быть реализовано
итерационными методами, такими как
кластеризация. Здесь предложен одношаговый
подход. Это предполагает, что каждый
класс описывается единственной компактной
конструкцией в пространстве функций.
Если дело обстоит не так, могут быть
применены другие методы, такие как,
например, реляционные классификации.
Подобный нечеткому алгоритму объединения
в кластеры, подход, предложенный здесь,
также предполагает, что форма нечетких
множеств может быть приближена
эллипсоидами. Таким образом, каждый
прототип класса представляет собой
центр
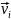его ковариационной матрицы
:
Здесь
i обозначает
индекс классов,
,
и
обозначает число образцов, принадлежащих
i-му
классу.
Шаг
2:
Вычисляется нечеткая матрица разделения
U,
ik-е
элементы которой,
,
являются степенью принадлежности
объекта данных
классу
.
Эта принадлежность основана на расстоянии
между высказыванием и центром класса:
Используя расстояние, принадлежность становится:
где m - весовой показатель, определяющий размытость полученных разделений (m = 1,8 применяется в примере).
Строки U теперь содержат поточечные представления многомерных нечетких множеств описания классов в пространстве функций.
Шаг
3:
Одномерные нечеткие множества
в классификации правил (1) получаются
путем проектирования рядов U
на входные переменные
,
а затем приближением проекций
параметрическими функциями. Для простоты
мы применяем треугольные нечеткие
числа:
Если используются более гладкая конструкция функции принадлежности, например, Гаусса или показательных функций, в результате модель будет в целом иметь более высокую точность в подгонке данных для обучения.