
- •Нечеткое моделирование: основные понятия и принципы
- •Задача нечеткой классификации
- •2.1 Постановка задачи.
- •Алгоритм решения
- •Формирование базы правил для нечеткого классификатора
- •3.1 Классификация нечетких моделей
- •3.1.1 Структура модели
- •3.1.2 Управляемая данными инициализация
- •3.2 Сокращение модели
- •3.2.1 Отбор свойств, основанный на межклассовой отделимости
- •3.2.2 Упрощение базы правил
- •Использование генетических алгоритмов для оптимизации
- •4.1 Основные понятия эволюционного программирования
- •4.1.1. Символьная модель
- •4.1.3. Кроссовер
- •4.1.4. Мутация
- •Постановка задачи
- •Мутация
- •Нечеткие операторы
- •Условие останова
- •Описание программы
- •Функциональные возможности
- •Представление данных
- •Реализация
- •1 Под продукцией понимается кортеж следующего вида:
СОДЕРЖАНИЕ
Введение…………………………………………………………………………..……….4
Нечеткое моделирование: основные понятия и принципы…………………….…...6
Задача нечеткой классификации……………………………………………….........13
Постановка задачи…………..………………………………………............…13
Алгоритм решения………………………………………………………..…....13
Формирование базы правил для нечеткого классификатора………….........…….15
Классификация нечетких моделей………………………………….…........….18
Структура модели…………………………………….……………………19
Управляемая данными инициализация…………………………..………20
Сокращение модели……………………………………………………..……..22
Отбор свойств, основанный на межклассовой отделимости……...…....22
Упрощение базы правил……………………………..………………..…..23
Использование генетических алгоритмов для оптимизации базы правил….…....25
Основные понятия эволюционного программирования..……….......…….….25
Символьная модель……………..……………………………….....………27
Канонический генетический алгоритм.……..…………………….………29
Кроссовер………………………………………….……………………….29
Мутация…...………………………………………...…………….………..30
Постановка задачи…….………………………………………………...…….…31
Алгоритм генерации базы знаний…………………………………………31
Получение «родительского элемента……………………………………32
Мутация……………………………………………………………………33
Нечеткие операторы………………………………………………………..33
Условие останова………………………………………………………….34
Описание программы……………………………………………………………….35
Функциональные возможности…………………………………………………35
Представление данных…………………………………………………………36
Реализация………………………………………………………………………37
Пользовательский интерфейс………………………………………………….38
Заключение……………………………………………………………………………….24
Список использованных источников…………………………………………………...25
ВВЕДЕНИЕ
Задача классификации является важной проблемой в различных областях знаний. Существует огромное количество исследований в этой области, приведших к большому разнообразию методов, которые все больше и больше применяются на практике.
Процесс разбиения объектов заданного множества на группы близких в некотором смысле, называется кластеризацией. Данное понятие тесно связанно с понятием классификации. Если известно количество групп, которые образуют разбиение, то кластеризация называется классификацией в широком смысле. Под классификацией в узком смысле понимается процедура отнесения заданного объекта к какой-либо группе.
Исследование методов классификации/кластеризации, основанных на знаниях, полученных от экспертов, в комбинации с наблюдаемыми данными, является перспективным направлением для решения подобных задач. Неотъемлемой частью экспертных систем, предназначенных для классификации/кластеризации, является база знаний. Необходимо отметить, что формирование базы знаний – чрезвычайно сложная проблема, поскольку необходимые и достаточные для решения данной задачи навыки приобретаются в процессе проектирования системы.
Нечеткие экспертные системы для поддержки принятия решений находят широкое применение в медицине и экономике. В настоящее время появляются пакеты программ для построения нечетких экспертных систем. Они применяются в автомобильной, аэрокосмической и транспортной промышленности, в области изделий бытовой техники, в сфере финансов, анализа и принятия управленческих решений и многих других.
В приложениях нечетких систем одной из важнейших задач является нахождение оптимального набора правил. Он может быть получен с помощью эксперта или априорным лингвистическим описанием моделируемой системы. Тем не менее, если ни эксперт, ни лингвистическое описание системы не доступны, оптимальный набор правил строится на основе численных данных. Природа подсказала нам алгоритмы оптимизации, применимые к нелинейным, многомерным и непрерывным задачам – эволюционные алгоритмы. Частным случаем эволюционных алгоритмов является генетический алгоритм – это алгоритм, который позволяет найти удовлетворительное решение к аналитически неразрешимым проблемам через последовательный подбор и комбинирование искомых параметров с использованием механизмов, напоминающих биологическую эволюцию.
Целью работы является создание программы, позволяющей на основе имеющихся данных (наблюдений) построить оптимальную базу знаний для систем нечеткого управления.
Нечеткое моделирование: основные понятия и принципы
Нечеткая система – это система, для описания которой используется аппарат теории нечетких множеств и нечеткая логика. Существуют следующие способы такого описания:
нечеткая спецификация параметров системы (функционирование системы может быть описано алгебраическим или дифференциальным уравнением, в котором параметры являются нечеткими числами);
нечеткое (лингвистическое) описание входных и выходных переменных системы, которое обусловлено неточной информацией, получаемой от ненадежных датчиков, или качественной информацией, получаемой от эксперта;
нечеткое описание системы в виде совокупности если-то - правил, отражающих особенности функционирования на качественном уровне.
Нечеткая система может иметь одновременно все перечисленные атрибуты. Нечеткие системы используются для моделирования, анализа данных, прогноза или управления.
Нечеткие правила – это нечеткие продукционные правила1, которые при фиксированной цели управления (например, сохранение значений управляемого параметра в некоторой области допустимых значений) описывают его стратегии на качественном уровне.
Рассмотрим основные приемы нечеткого моделирования систем. Для того, чтобы описать объекты и явления в условиях неопределенности, используют понятия лингвистической и нечеткой переменной.
Нечеткая переменная задается тройкой
, U, A,
где
–
название переменной, U
– универсальное множество (область
определения ),
А
– нечеткое
множество2
на U
с функцией принадлежности
 ,
описывающее ограничения на значение
нечеткой переменной.
,
описывающее ограничения на значение
нечеткой переменной.
Лингвистическая переменная задается кортежем
<, T, U, G, M>,
где
–
название переменной; Т
– базовое
терм-множество
или множество основных лингвистических
значений (термов) переменной ,
причем каждому из них соответствует
нечеткая переменная с функцией
принадлежности, заданной на U;
G
–
синтаксическое
правило,
описывающее процесс образования из
множества Т
новых значений лингвистической переменной
( называется расширенным
терм-множеством);
М
–
семантическое
правило,
согласно которому новые значения
лингвистической переменной ,
полученные с помощью G,
отображаются в нечеткие переменные
(это может быть процедура экспертного
опроса, позволяющая приписать каждому
новому значению, образованному процедурой
G,
некоторую семантику путем формирования
соответствующего нечеткого множества).
Шкала U,
на которой определена лингвистическая
переменная, может быть числовой или
нечисловой.
называется расширенным
терм-множеством);
М
–
семантическое
правило,
согласно которому новые значения
лингвистической переменной ,
полученные с помощью G,
отображаются в нечеткие переменные
(это может быть процедура экспертного
опроса, позволяющая приписать каждому
новому значению, образованному процедурой
G,
некоторую семантику путем формирования
соответствующего нечеткого множества).
Шкала U,
на которой определена лингвистическая
переменная, может быть числовой или
нечисловой.
Нечеткое
число
– это нечеткая переменная, определенная
на числовой оси функцией принадлежности
 .
Самые простые нечеткие числа –
треугольные и трапециевидные.
.
Самые простые нечеткие числа –
треугольные и трапециевидные.
Треугольным
нечетким числом А
с центром в точке а,
левой шириной
 и правой шириной
и правой шириной
 называется нечеткое множество А
с функцией принадлежности вида
называется нечеткое множество А
с функцией принадлежности вида


Трапециевидное нечеткое число А с отрезком толерантности [a,b], левой шириной и правой шириной задается функцией

Треугольное
нечеткое число с центром в точке а
можно рассматривать как нечеткое
значение высказывания х
приблизительно равен а,
в то время как трапециевидное число
обозначает нечеткое значение высказывания
х
находится приблизительно в интервале
[a,b].
Величины
l
и r
также называются соответственно левым
и правым коэффициентами нечеткости и
показывают насколько неточно (нечетко)
определены границы числа. Трапециевидное
нечеткое число обозначается кортежем
 ;
при
;
при
 получим треугольное нечеткое числа
получим треугольное нечеткое числа
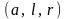 .
.
Рассмотрим
класс операторов пересечения и
объединения, известных как треугольные
нормы: t-норма
 и t-конорма
(s-норма)
и t-конорма
(s-норма)
 .
T
служит основой для определения пересечения
нечетких множеств, а S
– объединения нечетких множеств.
Принимая во внимание свойства классических
множеств, можно сформулировать следующие
свойства для t-норм:
.
T
служит основой для определения пересечения
нечетких множеств, а S
– объединения нечетких множеств.
Принимая во внимание свойства классических
множеств, можно сформулировать следующие
свойства для t-норм:
 – ограниченность
– ограниченность – коммутативность
– коммутативностьЕсли
 и
и
 , то
, то
 и
и
 – монотонность
– монотонность – ассоциативность
– ассоциативность
и для s-норм:
 граничные
условия
граничные
условия – коммутативность
– коммутативностьЕсли и , то
 и
и
 – монотонность
– монотонность – ассоциативность
– ассоциативность
где
 .
.
Другими
словами, функция
 есть t-норма
тогда и только тогда, когда она
удовлетворяет условиям T1-T4,
а
есть t-норма
тогда и только тогда, когда она
удовлетворяет условиям T1-T4,
а
 – s-норма
тогда и только тогда, когда она
удовлетворяет условиям S1-S4.
С точки зрения алгебры, T
– полугруппа в [0,1] с единицей 1, а S
– с единицей 0. Наиболее важные параметры
t-норм
и s-норм
приведены в таблице 1.
– s-норма
тогда и только тогда, когда она
удовлетворяет условиям S1-S4.
С точки зрения алгебры, T
– полугруппа в [0,1] с единицей 1, а S
– с единицей 0. Наиболее важные параметры
t-норм
и s-норм
приведены в таблице 1.
Таблица 1 – t-нормы и s-нормы
t-норма |
s-норма |
Заде
|
|
Алгебраическая
|
|
Лукашевич
|
|
Фодор
|
|
Глубокая
|
|
Теперь
введем оператор дополнения нечеткого
множества. Пусть в соответствии с
минимальными требованиями, необходимыми
для определения отрицания, мы имеем
невозрастающую функцию
 такую, что
такую, что
 .
Введем
следующие условия:
.
Введем
следующие условия:
n – строго убывающая
n непрерывна
 для
любого
для
любого
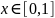
Отрицание строгое, если оно удовлетворяет условиям 1 и 2. Отрицание называется сильным, если для него также выполнено условие 3.
Наконец,
введем понятие импликации. Функция
 ,
удовлетворяющая следующим условиям,
называется импликацией:
,
удовлетворяющая следующим условиям,
называется импликацией:
Если
 ,
то
,
то
 монотонность по первому аргументу
монотонность по первому аргументуЕсли
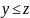 ,
то
,
то
 монотонность по второму аргументу
монотонность по второму аргументу

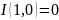
Наиболее важные нечеткие импликации представлены в таблице 2.
Таблица 2 – Нечеткие импликации
Название |
Вид |
Лукашевич |
|
Фодор |
|
Райхенбах |
|
Клине-Динс |
|
Заде |
|
Импликация применяется для получения нечеткого логического вывода. В его основе лежат классические схемы правильных рассуждений modus ponens и modus tollens.
Классический
modus
ponens
– это правило вывода следующего вида:
если посылки
 и
и
 истинны, то предпосылка
истинны, то предпосылка
 также верна, то есть
также верна, то есть
 ,
или:
,
или:
Предпосылка I – факт А
Предпосылка II – правило если A, то B
_________________________________
Заключение B
Нечеткая интерпретация позволяет перейти к обобщенному modus ponens, который может быть записан так:
Предпосылка I – факт А’
Предпосылка II – правило если A, то B
_________________________________
Заключение B’
где
 - нечеткие числа, определенные своими
функциями принадлежности на множестве
действительных чисел.
- нечеткие числа, определенные своими
функциями принадлежности на множестве
действительных чисел.
Пусть существует набор правил:


…
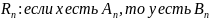

_______________________________

Каждому
правилу
 соответствует импликация
соответствует импликация
 .
Существует два подхода к формированию
функции принадлежности заключения:
.
Существует два подхода к формированию
функции принадлежности заключения:
Сначала все правила агрегируются, а затем применяется композиция.
Вначале формируется заключение для каждого правила вывода, а затем применяется оператор агрегирования.
Если получившееся множество B’ является нечетким, то возникает проблема определения конкретного числового значения выходной переменной. Для этого используется процедура дефазификации, которая представляет собой процесс перехода от лингвистического значения переменной к числовому значению на основе использования одного из следующих методов:
метод центра тяжести (Center of Gravity – COG):

метод центра площади (Center of Area – COA)

метод левого модального значения (Left Most Maximum – LM)

метод правого модального значения (Right Most Maximum – LM)

где
 – модальное значение нечеткого множества.
– модальное значение нечеткого множества.















