Лабораторная работа №3 Определение показателя адиабаты воздуха

3.1. Цель работы.

Закрепление знаний в теории исследования термодинамических процессов, ознакомление с методикой опытного определения показателя адиабаты реальных газов, получение навыков в проведении теплотехнического эксперимента.

3.2. Задачи работы

Экспериментальное определение численного значения показателя адиабаты воздуха и ознакомление с методами обработки результатов эксперимента.

3.3. Теоретические положения.

Адиабатный процесс является одним из наиболее часто встречающихся на практике термодинамическим процессом изменения состояния рабочего тела.

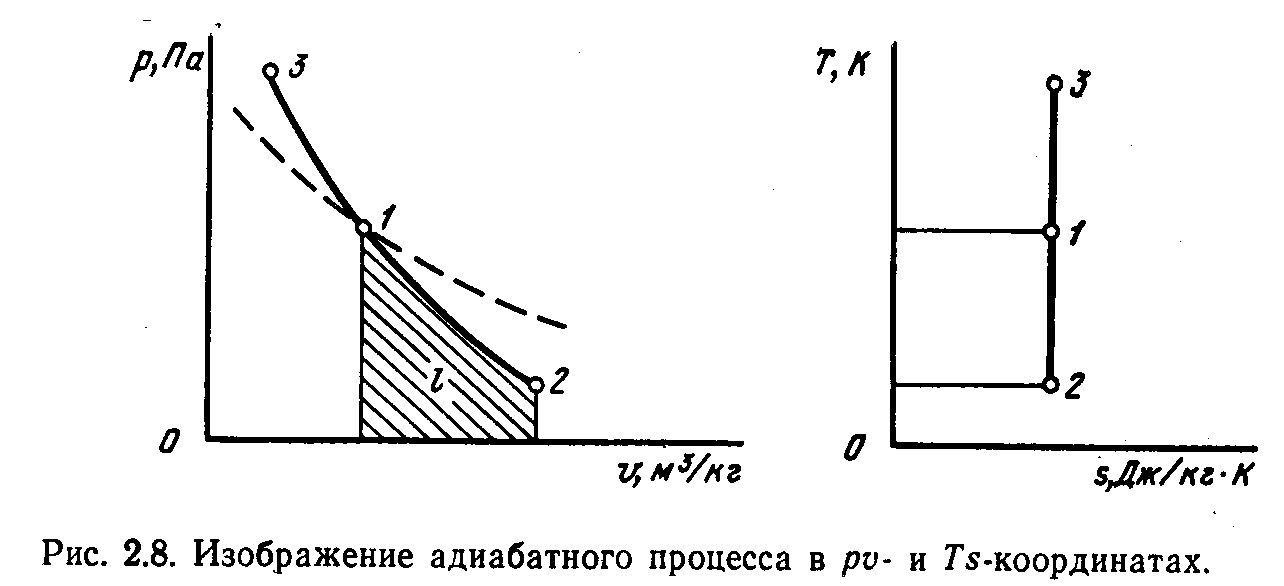
а) б)

Рис. 3.1. Изображение адиабатного процесса в р-v- и Ts- координатах

Адиабатный процесс — это процесс, протекающий без тепло­обмена с окружающей средой:

Δq=0 (3.1)

Уравнение адиабатного процесса имеет вид [1]:

(3.2)

где k - показатель адиабаты, равный отношению изобарной теплоемкости C_P к изохорной C_V:

>1 (3.3)

Численное значение показателя адиабаты для идеального газа можно получить исходя из молекулярно-кинетической теории газов:

для одноатомного газа k = 1,66

для двухатомного газа k = 1,4

для многоатомного газа k = 1,33

Для идеальных газов величина k является постоянной, не зависящей от параметров состояния газа.

Связь между изобарной и изохорной теплоемкостями устанавливает уравнение Майера:

С_P – С_V = R (3.4)

Выразив из (3.4) C_P, формулу (3.3) можно привести к виду:

(3.5)

Поскольку для реальных газов теплоемкость С_V возрастает с увеличением температуры интенсивнее, чем С_Р, то значение k с увеличением температуры уменьшается. Величина k для реальных газов одной атомности при прочих равных условиях имеет отличия. Так, например, для двухатомных газов: водород k=1,41; азот k=1,404; воздух k=1,4.

Поскольку k>1, то в р-v-координатах линия адиабаты идет круче изотермы.

Для адиабатного процесса характерны следующие соотношения [1]:

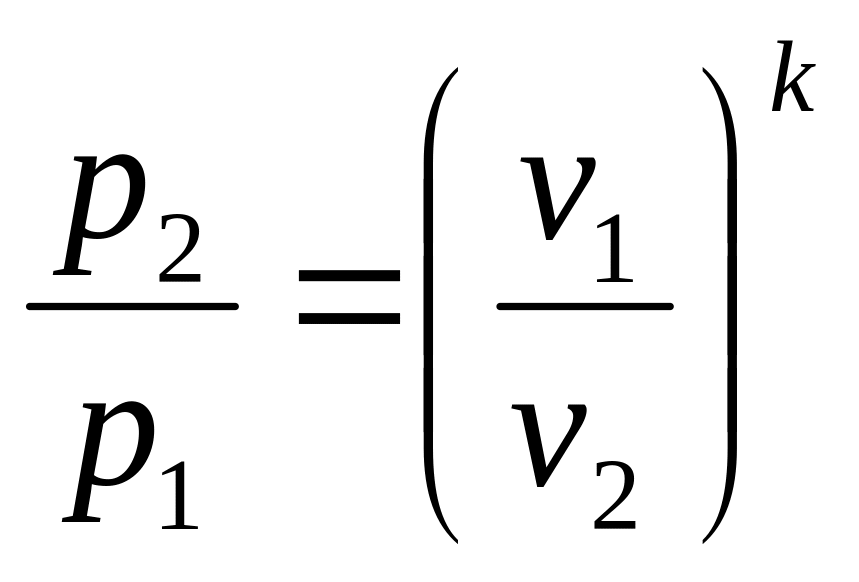
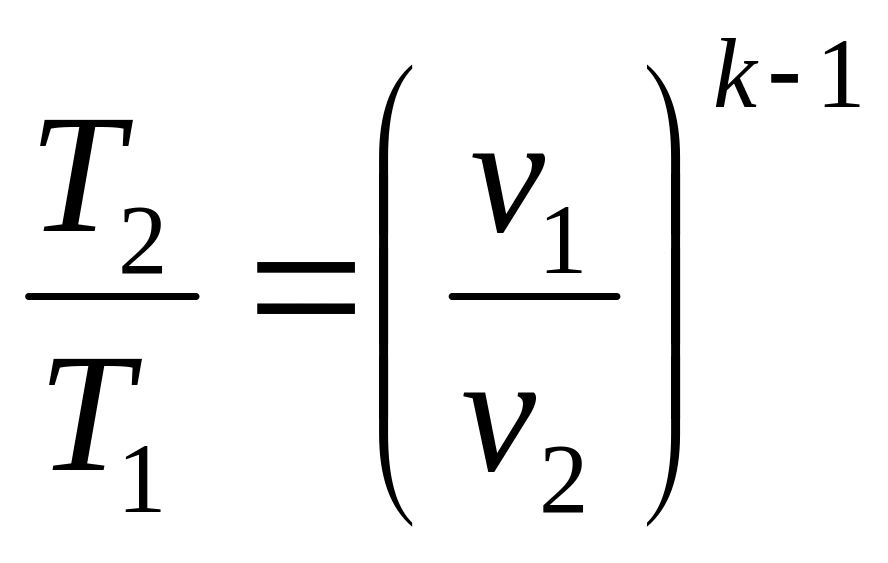
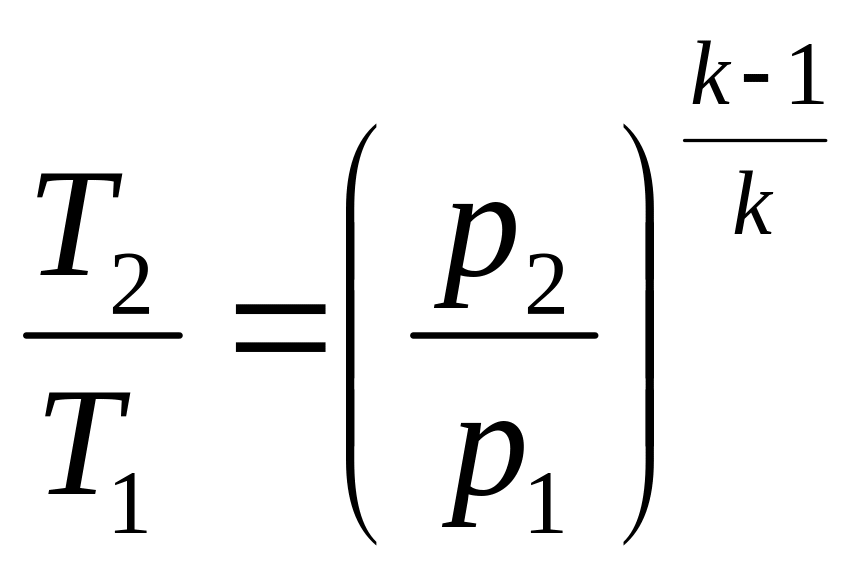(3.6)

Согласно первому закону термодинамики работа расшире­ния совершается за счет внутренней энергии:

(3.7)

Или (3.8)

После простых преобразований получаем:

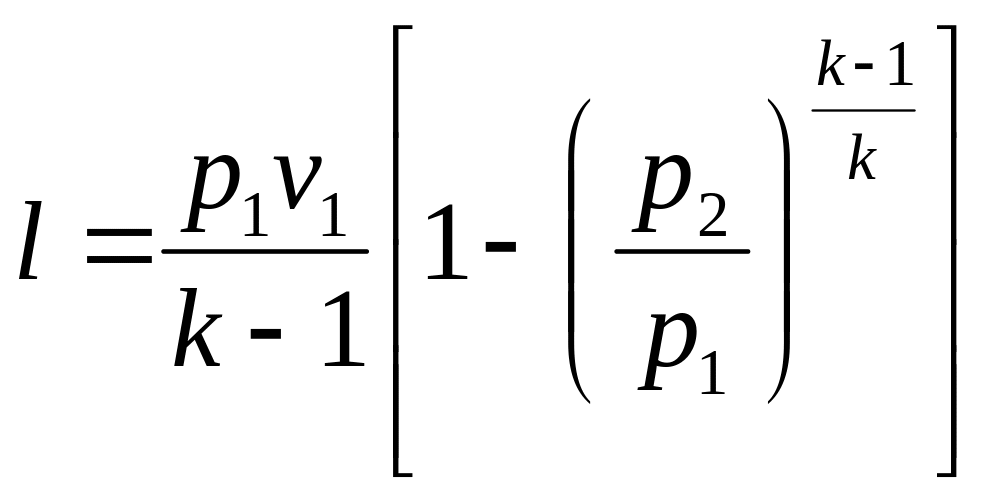(3.9)

Работа l численно равна площади под кривой 1—2 (рис. 3.1).

Поскольку при адиабатном процессе Δq=0, то ds=0, следо­вательно, s=const. Адиабатный обратимый процесс является изоэнтропным, т. е. протекает при постоянном значении энтро­пии. На рис. 3.1 линия 1—2 соответствует расширению ра­бочего тела (процесс сопровождается уменьшением темпера­туры), а линия 1—3—сжатию рабочего тела.

При адиабатном процессе тепло­емкость равна нулю C_АД=0.

Допустим, что условия опыта с достаточной степенью точности удовлетворяют уравнению состояния идеального газа:

p·v=M∙R∙T (3.10)

Представим сосуд, заполненный газом, имеющим параметры: давление P₁ и температуру Т₁, превышающие параметры окружающей среды. За счет охлаждения стенок сосуда окружающей средой и отвода некого количества теплоты q₁, температура газа станет равной температуре окружающей среды – Т₂, а давление снизится до некого значения Р₂ (процесс 1-2 рис.3.2 [6]). Затем быстро выпустим газ из резервуара, соблюдая тем самым условия адиабатного расширения - отсутствие теплообмена с окружающей средой. В конце этого процесса (2-3) давление в сосуде станет равным давлению окружающей среды Р₃, а температура понизится до Т₃, меньше Т₂. Закроем сосуд и выждем некоторое время, в течении которого от окружающей среды к более холодному телу будет подведена теплота q₂ (процесс 3-4).

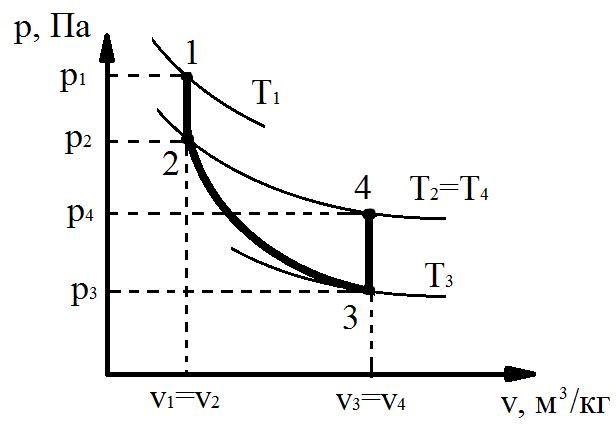
Рис.3.2 К определению показателя адиабаты

В результате температура возрастет до температуры окружающей среды (Т₄ =Т₂), а давление повысится до некоторого значения Р₄.

Учитывая уравнение адиабатного процесса (3.2) можно записать:

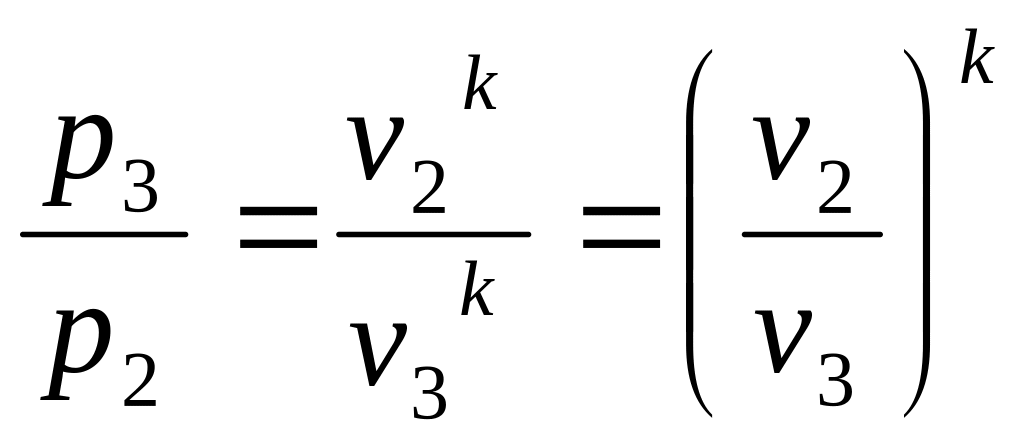(3.11)

Выведем отсюда k:

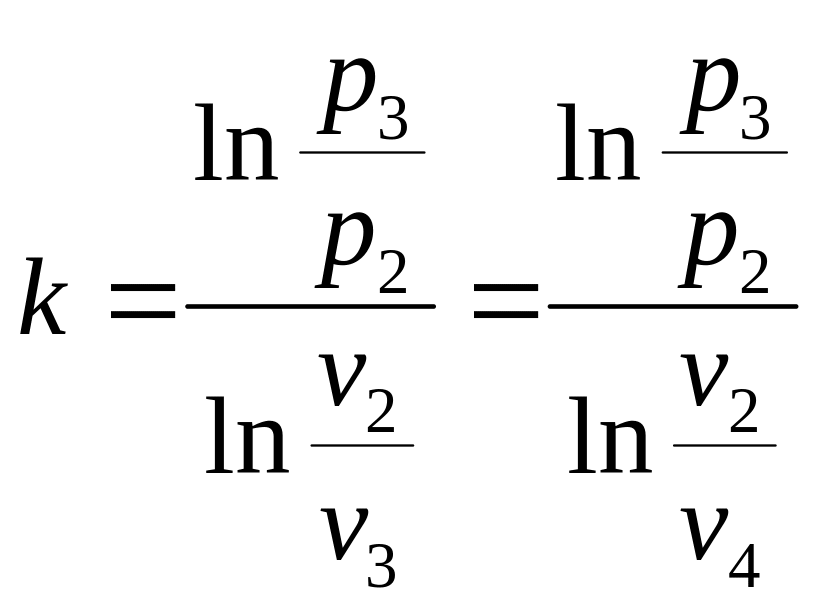(3.13)

Так как Т₂=Т₄, можно предположить, что по линии 2-4 протекает условный изотермический процесс (Т=const), которому соответствует выражение:

(3.14)

С учетом выражения 3.14 уравнение 3.13 примет вид:

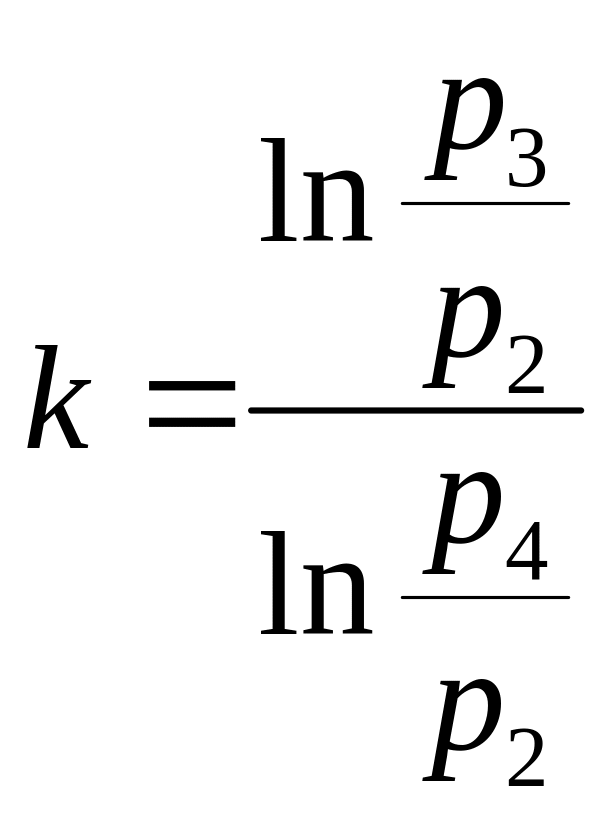(3.15)