3 IV ажжк-да қолданылатын қос тұтылмалы жүйелердің кластары

Тұтылмалы айнымалы жұлдыздың жарқырау қисығының сипаты бойынша қос жұлдыздың біреуінің екіншісіне қатысты орбита элементтерін анықтауға болады. Жарқырау қисығын мұқият зерттеу нәтижесінде тұтылған айнымалы жұлдыздар туралы келесі мәліметтер алынады:

1. Тұтылу сипаты көлбеулік бұрышы мен жұлдыздың өлшемдері көмегімен анықталады: i = 90^ºболғанда тұтылу орталық болады.

2.Минимумдардың ұзақтығының негізінде компоненттердің  R₁және R₂радиустарын табуға болады

3. Егер тұтылу толық болса, онда минимумдар тереңдігенің қатынасы арқылы жарықтылықтар қатынасын анықтауға болады, ал егер радиустары белгілі болса онда температуралардың қатынасын анықтай аламыз.

4. Жарқырау қисығының көлбеулік сипатынан жұлдыздар сәулеленулерінің өзара шағылуларын сипаттауға болады.

5. Жарқырау қисығының минимумдарын мұқият зерттеу нәтижесінде жұлдыз дискінің шетіне қарай қараңғылау заңын бағалауға болады.

Сонымен, жарқырау қисығының нәтижесінде келесі шамаларды анықтауға болады екен: i- орбита жазықтығының көлбеулік бұрышы, Р– айналу периоды,  Т– бас минимум кезеңі, е– орбита эксцентриситеті, w - периастр бойлығы,  R₁,R₂- компоненттердің радиустары, L₁/L₂- жарықтылықтар қатынасы.

Біз тығыз қос тұтылмалы жүйелердің компоненттерінің жарқырау қисығының формасына, физикалық және эволюциялық сипаттамасына қарай үшөлшемді топтастыру жүйесін қабылдаймыз. Жарқырау қисығы бойынша топтастыру бақылаушы үшін қарапайым және жеңіл; екінші және үшінші тәсілдері Mv, В – V диаграммасында қос жүйе компоненттерінің орналасуына және компоненттердің ішкі Рош қуысын толтыру дәрежесі бойынша топтастыру. Бұл үшін М.А.Свечников пен Л.Ф.Истоминый (АЦ№ 1083, 1979) ұсынған қарапайым критерилер қолданылады. ІV АЖЖК-да қолданылатын қос тұтылмалы жүйелердің типтерінің символдарына тоқталайық.

а) Жарқырау қисығының пішіні бойынша топтастыру.

Е- тұтылмалы қос жүйе. Орбита жазықтығы бақылаушының бейнелік жазықтығына жақындығы сонша (орбита жазықтығының бейнелік жазықтыққа көлбеулігі 90° жақын), екі компонента (немесе біреуі) периодты түрде бірін-бірі тұтып отырады. Осының әсерінен бақылаушы жүйенің көрінерлік жарқырауының өзгерісін байқайды

ЕА – Алголь ((бета) Per) типіндегі тұтылмалы айнымалылар. Сфералық немесе кішкене эллипсті компоненттері бар қос-тұтылмалы жұлдыздар.

Жарқырау қисықтары тұтылудың басталу мен аяқталу моменттерін белгілеуге мүмкіндік береді. Тұтылулар аралығында жарқырауы шамамен тұрақты болады немесе шағылу эффектілерінен, компоненттердің эллипсті болуынан немесе физикалық өзгерістерден аз ғана өзгереді. Екінші ретті минимум байқалмауы мүмкін. Периоды 0.2-ден 10000d-ға дейінгі өте кең аралықта және одан да көп аралықта өзгереді, жарқырау өзгерісінің амплитудасы әр түрлі және бірнеше шамаға жете алады.

1.3.1- сурет. ЕА – Алголь ((бета) Per) типіндегі тұтылмалы айнымалылар.

1.3.2- сурет. Фотоэлектрлік бақылау негізінде алынған Алголь жұлдызының дербес тұтылу кезіндегі жарқырау қисығының өзгерісі.

Р- период

Бұл суретте Алголь жұлдызының жарқырауының 2 рет кемуі көрсетілген. I- минимум- негізгі тұтылу, II-минимум – жарқырауының баяу бәсеңдеуі.

Жарқырауының баяу бәсеңдеуі кезінде ең жарық компонент әлсізін жауып қалады. Бұл жағдай 2,8674 тәулікте қайталанады.

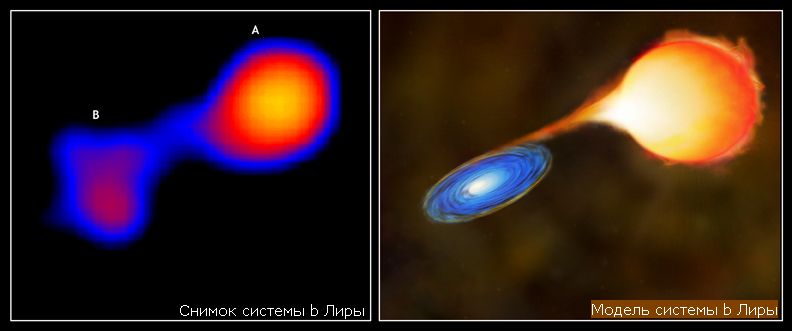
EB – (бета) Лира ((бета) Lyr) типінің тұтылмалы айнымалылары. Компоненттері эллипсті қос-тұтылмалылар. Тұтылудың басы мен соңын (тұтылулар аралығында жүйенің көрінетін қорытынды жарқырауының үздіксіз өзгеру себебінен) анықтауға мүмкіндік бермейтін жарқырау қисықтарына ие. Тереңдігі негізгі минимумнан біршама кіші болатын екінші ретті минимум міндетті түрде байқалады. Периодтары 1d-дан біршама көп (1d-дан кіші периодтарда әр түрлі тереңдіктің минимумдары болады, 1d-дан жоғары периодтарда минимумдар тереңдіктері шамалас болуы мүмкін), компоненттері негізінен B-A ерте спектрлік класстарына тиісті. Жарқыраудың өзгеру амплитудалары негізінен 2m V-дан кіші

1.3.3- сурет. β Лира типіндегі қос-тұтылмалы жүйе

.

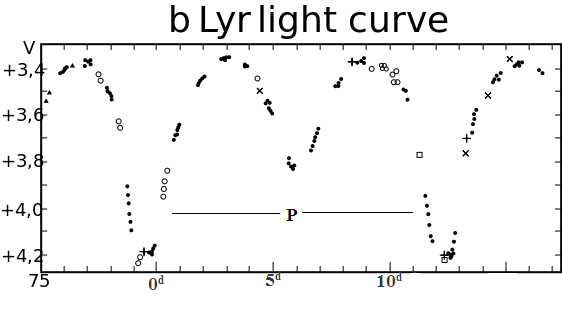
1.3.4- сурет.  Лира жұлдызының жарқырау қисығының өзгерісі

EW – W Үлкен Аю (W UMa) типінің тұтылмалы айнымалылары. Периоды 1d-дан кіші, жанасып орналасқан эллипсті компоненттерден тұратын, тұтылулардың басы мен аяғын анықтауға мүмкіндік бермейтін жарқырау қисығына ие қос-тұтылмалы жұлдыздар. Негізгі және екінші ретті минимумдардың тереңдіктері шамалас және қатты айырмашылығы жоқ. Жарқырауының өзгеру амплитудасы негізінен 0.8 mV-нен кіші. Компоненттерінің спектрлік класстары F-G және одан кештері.

1.3.5- сурет. W Үлкен Аю типінің тұтылмалы айнымалылары.

1.3.6- сурет. W Үлкен Аю типіндегі тұтылмалы айнымалылардың жарқырау қисығы.

б) Компоненттердің физикалық сипаттамалары бойынша топтастыру

GS – бір компонентасы немесе екі компонентасы да гигант немесе аса жоғары гигант болып келетін жүйелер. Компоненттерінің біреуі бас тізбектен болуы мүмкін.

PN –компоненттері планерлық тұмандықтардың ядролары (UU Sge) болып табылатын жүйелер.

RS - RS Қуғын Иттер (RS CVn) типінің жүйелері. Бұл жүйелердің ерекшелігі - спектрлерінде H пен K Ca II күн типтес жоғары хромосфералық активтілігін куәландыратын айнымалы интенсивтіліктің күшті эмиссионды сызықтарының болуы. Бұл жүйелерге радио және рентген сәуле шығарулар тән. Бұлардың кейбірінің жарқырау қисықтарында тұтылудан тыс, уақыт өтумен амплитудасы мен орны баяу өзгеретін квазисинусоидалы толқын байқалады. Бұл толқынның (жиі дисторсионды аталатын) пайда болуы бетінде дақ топтары бар жұлдыздың дифференциал айналуымен түсіндіріледі. Дақ топтарының айналу периоды орбитал қозғалыс периодына (тұтылу периодына) жақын, бірақ сонда да одан айырмашылығы бар. Сондықтан бұл ортаңғы жарқырау қисығында дисторсионды толқынның минимум мен максимум фазаларының баяу өзгерісін (миграциясын) тудырады. Толқынның амплитудасының өзгермелі болуы (0.2m V-ге жететін) жұлдыз бетіндегі дақтардың жалпы ауданы мен саны өзгеретін аралықтың - жұлдыздық активтіліктің ұзақпериодты циклінің болуымен түсіндіріледі.

WD – компоненттері ақ ерегежейлілер болып келетін жүйелер.

WR – компоненттерінің арасында Вольф-Райе (V 444Cyg) типіндегі жұлдыздар кездесетін жүйелер.

в) Рош қуысының толтырылуына байланысты топтастыру

AR - AR Кесіртке (AR Lac) типінің бөлінген жүйесі, екі компонентасы да өзінің ішкі эквипотенциальді қуыс бетіне жетпеген субгигант.

D - компоненталары өзінің ішкі эквипотенциальді Рош қуысының бетіне жетпеген, бөлінген жүйелер.

DM – бас тізбектің бөлінген жүйелері, екі компонентасы да өзінің ішкі эквипотенциальді Рош қуысының бетіне жетпеген бас тізбек мүшелері.

DS – субгигантпен бөлінген жүйелер, бұл субгигант та өзінің ішкі эквипотенциальді қуыс бетіне жетпеген.

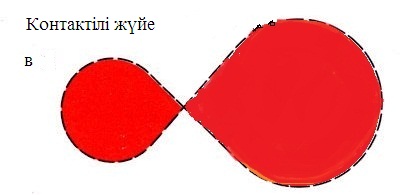
  К –контактілі жүйелер, екі компонентасы да өзінің ішкі эквипотенциальді Рош қуысының бетін толтырған.

КЕ – ерте спектральді классқа жататын (О-А) контактілі жүйе, екі компонентасы да өлшемі бойынша өзінің ішкі қуысына жақын.

КW – WUMa типіне жататын эллипсоидальді компоненталардан тұратын, спектральді класы F0-К болатын контактілі жүйелер. Басты компонентасы бас тізбек мүшесі, ал серігі Mv, В – V диаграммасында одан төмен және солға қарай орналасқан.

SD – массивті компонент-субгиганттың беті өзінің ішкі қуысына жақын орналасқан жартылай бөлінген жүйелер.

Тұтылмалы айнымалы жұлдыздар

Тұтылмалы айнымалы жұлдыздардың классификациясы

Ең алғашқы тұтылмалы айнымалы жұлдыз Алгольды (β Персей) 1669 жылы итальян математигі мен астрономы Монтаранимен ашылды. XIII ғасыр аяғында ағылшын астрономияға қызығушы Джон Гудрайк зерттеді. Адамның көзі жалғыз β Персей жұлдызын байқады, телескоппен бақылағанда (кратная) жұлдыздық жүйені орналасқан. Жұлдыздық жүйеге кіретін екі жұлдыз қос тығыз (пара) құрайды. Масса центрінің айналасында бір орбиталық айналымды 2 тәулік 20 сағат 49 минут жасайды. Уақыттың белгілі бір моментінде бір компоненті жерден бақылаушыға жауып қалады, бұл жүйенің қорытқы жарқырауының уақытша кемуіне әкеліп соғады.

4 суретте Алголь жұлдызының жұлдыздық шамасының жарқырау өзгерісінің айырымы мен дәл фотоэлектрлік бақылауға негізделген жарқырауы тұрақты салыстырушы жұлдыз үшін берілген. Суретте екі жарқырауының кемуі көрінеді: терең бірінші минимум- негізгі тұтылу, және (ақырын жай) жарқырауының кемуі бәсендеу – екінші минимум. Соңғы жағдайда ең жарық компоненті жарқырауы бәсенің жауып қалады. Бұл құбылыстар 2,8674 тәулікте қайталанады (2 тәулік 20 сағат 49 минут). Алголь жұлдызы үшін ең төменгі жарқырауға жеткен соң оның көтерілуі тез арада басталады. Бұл дербес тұтылу болатындығын білдіреді. Егер толық тұтылу болатын болса, онда минимумның орта шенінде толық фаза байқалады, белгілі бір уақыт аралығында жарқырау өзінің ең кіші мәнің сақтайды. Тұтылу болмаған жағдайда жұлдыздың жарқырауы тұрақты болуы тиіс, бұл уақытта жарық бізге екі компоненттен де келеді. Бірақ екі компоненте бір-біріне жақын орналасқандықтан жарық компонентамен жарықтанатын, ең әлсіз компонентасы (көбінесе өлшемі бойынша үлкен) өзіне түсетін сәулені шашыратады. Шашыраған сәуленің көп мөлшері жердегі бақылаушыға бағытталады, екінші тұтылуға жақын орналасқан бұл компонента жарық компонентадан орналасады. Бұл құбылыс 4 суретте көрінеді. Жүйенің жалпы жарқырауы екінші минимумға жақындағанда аздап өседі және одан кейін симметриялық түрде кемиді.

Бұл уақытқа дейін бұған ұқсас жүздеген айнымалы жұлдыздар ашылған және зерттелген. Бұлар Алголь типтегі жұлдыздар болып классикацияланады.

1784 жылы Гудрайк екінші тұтылмалы айнымалы жұлдызды – β Лираны ашты. β Лира жарқырауын салыстырмалы түрде баяу периодпен өзгертеді 12 тәулік 21 сағат 56 минутқа тең (12.914 тәулік). Алгольмен салыстырғанда өз жарқырауын (плавно) өзгертетіні екі компонентаның жақын орналасқанын білдіреді. Жүйеде пайда болатын тасу қайту (приливные) күштері центрлерін біріктіретін екі жұлдызды бір сызық бойында тартылуына әкеледі. Бұл жағдайда компонентері шар тәрізді емес, эллипс тәрізді болады. Орбиталық қозғалыс барысында эллипстік формадағы компонент дискілері ақырындап өз ауданын өзгертеді, бұл жұлдыздың тұтылу болмаған жағдайда үздіксіз жарқырауының өзгеруіне алып келеді. Бұл өзгерістің заңдылығын зерттеу компонент формасы жөнінде салыстырмалы қорытынды жасауға болады.

1903 жылы W Үлкен Аю тұтылмалы айнымалы жұлдызы ашылды, периоды 8 сағаттан асатын (0,3336384) Бұл уақыт аралығында бірдей немесе тең болатындай тереңдіктегі екі минимум байқалады (6 сурет). Мұндай жұлдыздың жарқырау қисығын зерттеу компоненттер өлшемдері бойынша бірдей және бір –бірімен беттерімен жақындасады. Алголь типтегі, β Лира, W Үлкен Аю тұтылмалы айнымалы жұлдыздарынан басқа өте сирек кездесетін объектілер бар. Өз осіне қатысты айналатын эллипс тәрізді жұлдыздар. Дискінің ауданының өзгерісі жарқырауының аз өзгерісіне әкеледі.

Алголь типті тұтылмалы айнымалы жұлдызды зерттеу неге алып келеді?

Жарқырау қисығының өзгерісін математикалық өңдеу екілік жүйе туралы көп ақпаратты береді.Мысал келтірейікекі компонент те шартәрізді және жалпы массалар центрінен дөңгелек орбитамен қозғалады деп есептейміз. Егер m₁ деп массасын, a₁ бірінші компоненттін орбитасының радиусын, m₂ екінші компонент массасы, a₂ - екінші компоненттін орбитасының радиусын белгілейміз, онда массалар центрлер анықтамасынан

m₁ a₁ шығады.

Массалар центрі екі компоненттің аралығында орналасқандықтан, массаларына кері пропорционал. Салыстырмалы орбитаның радиусын яғни екі компоненттің центрлерінің арақашықтығын белгілейміз

Бірінші компонент радиусын R₁ , ал екінші компонент радиусын R₂ белгілейміз. Онда қатынас

Жүйенің екі элементі болып табылады.

E₁ –бірінші компонента жарқырауы, E₂ –екінші компонента жарқырауы, тұтылу болмаған жағдайдағы толық жарқырауы

Соңғы қатыснасты E –ге бөліп, келесі белгілеуді енгіземіз.

Бұл жүйенің үшінші және төртінші элементтері. Бұлар келесі қатынаспен байланыста. Жүйенің бесінші элементі – көрінерлік сәулеге перпендикуляр жазықтық –бейнелік жазықтық деп аталады. Екілік жұлдыздың салыстырмалы орбитасының жазықтығын бейнелік жазықтықты түзу сызықпен қияды – түйіндер сызығы д.а. Орбита жазықтығы бейнелік жазықтыққа i бұрышымен көлбеуленеді – орбита көлбеулігі д.а. Бұл орбитаның бесінші элементі. Тұтылмалы айнымалы жұлдыздар үшін көлбеулік i 90⁰ көп өзгермейді, әйтпесе тұтылу болмас еді.

Жарқырау қисығының өзгерсінен барлық бес элементті анықтауға болады. Толық тұтылу болған жағдайда нақты сенімді түрде анықталады.

l₁ мен l_ә анықтаудан бастайық. Бірінші компоненттің радиусы R₁ үлкен бірінші минимум уақытында кіші екінші компоненті радиусы R₂ бірақ жарығырақ толығымен жабады. Тұтылу болмаған жағдайда жүйенің толық жарқырауы E , жарқырауы максимум болғанда жұлдыздық шамасы m₀ болсын. Толық фаза кезеңінде біз жарықты тек үлкен жұлдыздан қабылдаймыз, оны E₁ деп белгілейміз. Онда толық фаза кезінде жұлдыздық шамасы m₁

r₁ мен r₂ элементтерін анықтау күрделірек, себебі орбита көлбеулігін анықтау керек. Орбита көлбеулігін анықтау әдісі бар, бірақ біз есепті жеңілдетеміз, бірнеше ауытқумен көлбеулікті i=90° деп есептейміз. Тұтылу тек толық емес, сонымен қатар центрлік деп есептейміз 8-суретте компонент дискілерін екі орнында тұтылудың екі жағдайын (сурет 8 а) тұтылу бастапқы мезетінде (сурет 8 б) оның толық тұтылу фазасындағы бастапқы моментінде центрінен

Үлкен жұлдыз дискісі штрихпен жабылған; тұтылу кезеңінде кіші компонента үлкен компонентаның арғы бетіне орналасады.

Тұтылудың бастапқы моментінде компонент дискілері сыртқы беттері бір-біріне түйіседі. Дискілер центрінің ара қашықтығы Δ₁=R₁+R₂ тартылу бас мезетінде сәйкесінше орбитадағы бұрышы θ₁

,.

Толық фазаның тұтылудың басталуында компонент дискілері ішкі түйісуден тұрады, екі центрдің ара қашықтығы орбитадағы Δ₂=R₁-R₂ толық фаза бастапқы моментінде сәйкес бұрыш θ₂. Орбитаның салыстырмалы радиусын а деп белгілеп, үшбұрыштан келесіні айтамыз.

R₁+R₂=a sin θ₁

R₁-R₂=a sin θ₂

теңдікті а-ға бөліп, R₁/a=r₁, R₂/a₂=r₂ (11) формуланы ескеріп,

r₁+r₂=sin θ₁ ,

r₁-r₂=sinθ2 } (12)

r₁ мен r₂-ге қатысты бұл теңдіктерді шешу үшін θ₁ мен θ₂ бұрыштарын білу керек, оларды жарқырау қисығының өзгерісінен анықтайды.

Егер орбита дөңгелек болса, онда орбита бойымен жылдамдығы тұрақты, Р период аралығында 360°-ке өсе отырып θ бұрышы уақытқа пропорционал өседі. Тұтылу ұзақтылығын D мен толық фаза ұзақтығын d период бөлігінен белгілеп, анықтаймыз.

Енді (12) теңдеуді

2 θ₁=360°D,

2 θ₂=360°d (13)

шешіп r₁ мен r₂ мәндерін алуға болады. U Цефей жұлдызына (12) мен (13) формулаларды қолданып, жарқырау қисығынан D=0.160 мен d=0.039 онда θ₁=28°30 және θ2=7°02 , sinθ1=0.48175, sinθ2=0.12222 . Теңдеуді шешіп r₁=0.302 мен r₂=0.180 жүйенің барлық элементтері анықталады, бірақ бұл аяқталған жоқ. Қос жұлдыздың бірқатар ерекшеліктеріне тоқталайық. r₁ мен r₂ радиустар қосындысы 0.482-ге тең, центрлер ара қашықтығы бірлікке тең деп есептелінеді. Жұлдыздар беттерінен ара қашықтығының бөлігіне 0,518 қалады. Екілік жүйені "тығыз" деп атауымызға негіз бар.

Үлкен жұлдыз радиусы r1=0.302 жүйенің жалпы сәулеленуінен жұлдыздық сәулеленуіне l1=0.0545 бөлігіне кетеді. Кіші жұлдыз жоғары жарықтылыққа ие. Компоненттер аралығындағы сәулеленудің тартылуы олардың температураларының бірдей еместігінен жұлдыз дискілерінде жарқырауының таралуы жөнінде қарапайым жорамал қабылдаймыз ("U-гипотеза ") дискі центрі мен шетінде жарқырауы бірдей деп есептейміз. Бірінші компонента дискісінің жарықтылығы I₁, 2-шісін I₂ белгілейміз. Бірінші компонента жарқырауы L₁= π , екіншісі L₂=π олардың қатынасы

Жарықтылық температураның 4-ші дәрежесіне пропорционал деп жуықтап алып Т₁/Т₂=0,378. Максимум жарқырауда U-Цефейдің спектр класы В8V онда оның температурасын Т₂=12000°. Онда T₁=4540°, бірінші минимум жарықтылықта спектр класпен G8III жақсы сай келеді, онда бізге жарық үлкен компонентадан-субгиганттан келеді.

Жарқырау қисығының өзгерісінен жүйенің абсолютті өлшемін, компонент массасын анықтауға болмайды. Бұл үшін спектральдық бақылаулар -жұлдыздардың сәулелік жылдамдықтарын анықтау қажет. Спектр сызықтарының ығысуына байланысты көріну сәулесінің бойымен сәуле (қозғалысының ) көзінің қозғалыс жылдамдығын анықтауға болады. (9-cуреттен компоненттердің орбита қозғалысында жылдамдықтың проекциялары көріну сәулелеріне орбитадағы орнына тәуелділігі периодты түрде өзгереді). U- Цефей жүйесіндегі сәулелік жылдамдықтар өзгерісі 10-суретте келтірілген. Жарық компонентаның бақылаудан алынған сәулелік жылдамдығының мәндері нүктелермен белгіленген, жылдамдықтың өзгеріс қисығы - біртұтас сызықпен берілген. Ең үлкен ауытқу жылдамдығы екі тәулікке жуық уақытта бақыланады. (+135км/с) (жарқырау минимум болғандағы деп есептегенде). Ең үлкен жақындау жылдамдығы (-110км/с)- үш тәулікке тең уақытқа тең. Үзіліссіз сызықтың пунктирмен белгіленген қисықтық бір бөлігі көрінбейді. Бұл үзілу жарық компонентасының тұтылуына сай келеді (спектрі көрінбеген кезеңдегі).

Кіші жарық компонентасының сәулелік жылдамдығының өзгерісінің жартылай амплитудасы 135+110/2=122~120 км/с. Бұл мәнді v₂ орбита бойымен жылдамдығы деп есептейміз. Тұтылу барысында ең әлсіз компонентаға сай келетін спектр сызықтар көріне бастайды. Ең әлсіз компонентаның бақыланған сәулелік жылдамдықтары айқас сызықтармен белгіленген, көлбеу үзік сызық осы сәулелік жылдамдықтың қисығының кесіндісін береді. Осы кіші кесінді бойынша 200 км/с-ке жақын екінші компонентаның орбита бойымен қозғалыс жылдамдығын v₁-ді бағалауға болады. Сызықтардың периодты ығысуымен анықталатын жұлдыздар спектральді қос деп аталады. Жарқырауының минимум болған моментінде екі компонента да орбита бойымен көріну сәулесіне перпендикуляр бағытта қозғалады. Сондықтан минимум моментінде сәулелік жылдамдықтар нольге тең. θ бұрышы 90° пен 270° аралығында сәулелік жылдамдықтар абсолют мәндер бойынша ең үлкен мәнге жетеді. Орбита жазықтығының көлбеулігін ескеріп әр компоненттің орбитадағы қозғалыс жылдамдығын анықтауға болады. Компоненттер орбитасын дөңгелек деп есептеп, а₁ мен а₂ радиусымен, периодты Р секундпен өрнектеп, орбита бойымен жылдамдығын v₁, v₂-ны км/с анықтаймыз.

а₁=P v₁/2π , а₂=P v₂/2π

10-суреттен v₁=200 км/с, v₂=120 км/с. Период Р=2,493 тәул=215395c. Сәйкесінше а₁=6,856* км және а₂=4,114* км. Сондықтан (11) формулаға сәйкес салыстырмалы орбитаның үлкен жарты осі a=a₁+a₂=10,97* км.

Енді (11) формула көмегімен компонент радиустарын анықтауға болады

=a =3,31* км

=a =1,97* км

Күннің радиусы =0,696* км, онда компонент радиусы =4,76 , =2,84

Кеплердің үшінші заңы бойынша компонент массаларының қосындысы + = (14) -гравитациялық тұрақты, жүйенің өлшеу бірлігіне тәуелді.

Егер арақашықтықты млн км-мен, массасын - Күн массасымен, периодын тәулікпен қарастыратын болсақ, онда жүйенің жалпы массасы + =0,00398 , a=10.97, =2.493 + =8.45, (9) формуламен массалар қатынасын

/ = / =1.665,

бұдан =3.17 мен =5.28 Күн массасымен. Алынған нәтижелерден екі жұлдыздың орташа тығыздығын анықтауға болады.

Жұлдыз массасы Күн массасымен, радиусы Күн радиусымен белгілі болғандықтан ρ , Күн затының орташа тығыздығы =1,41г/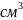 , кіші жарық компонентаның =0,32 г/ , үлкен компонента бірақ жарықтылығы әлсіз 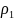=0,04г/

U Цефей жұлдызының тығыз екілік жүйенің ең негізгі параметрлерін анықтадық.

ққұ

ұқұңқұғ

қққұңәүңққққәұғқәүққәәүқұқққққұңқүқққө

 ^

ққққөұғәқққққұңұ

_^{}

^{} ^

ө



өөұқққұққғұңқғұңқүңүңүқүңқүңүұқұңқғқәүұқ^ңңғқө



ұңқғңұқұңңғқ^ңқғәәғұң^үңғңқңңөұқғ^

қә

^



қ

^^

ұөүөқөңғұққ

^

ң_{}^

өқққққұқұқұғққққ





әғқңұ

қ



қққ

қ

ңғқұңұңұ

ұққәңөғұңқғғәққғәқөңқғөәқәққғ

∆_

_әқ

қғ

қғқұғ

∆қғ

ққөғңқғғқғүұғөәұңқғқ

ұәққғңәңүәұңңққғүұққұғқұғңқұұүңәқұқғұққәққұң