5. Жазықтықтың теңдеулерінің түрлері. Нүктеден жазықтыққа дейінгі арақашықтық. Екі жазықтықтың арасындағы бұрыш.

Жазықтықтың теңдеулерінің түрлері

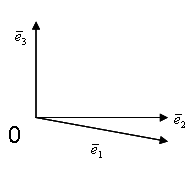
Жазықтықта жататын кез-келген 2 коллиниар емес вектор оның бағыттауыш векторлары деп аталады. Жазықтықтың теңдеуін жазу үшін 3 нәрсе к/к.: 1нүкте ж/е 2 бағыттауыш вектор.

жазықтық

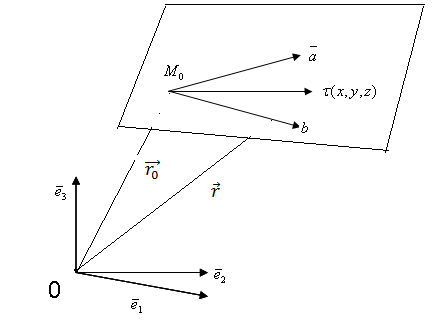
, бағыттауыш вектор

,бағыттауыш вектор,

, параллел емес векторлар

-ағымдағы нүкте

- =

( , )- базис

;

-

= - жазықтықтың векторлық, параметрлік теңдеуі

(2) жазықтықтың координаттық, параметр-к теңдеуі.

компланар векторлар болуы қажетті және жеткілікті

( , )=0

=0 (3)

Жазықтықтың жалпы теңдеуі

Теорема: 1) Аффин координат-р жүйесінде кез-келген жазықтықтың теңдеуі кеңістікте бірнеше дәрежелі теңдеумен жазылады.

(4)

2) Кез келген (4) түрдегі теңдеу кеңістікте жазықтықты анықтайды.

Д/у: 1)дәлелдеу үшін (3) пен (4) тің байланысын табу керек.

(3) =>(4) (3)ті 1-қатар бойынша жіктейміз.

=0

=А =В =С

=> Ax+By+Cz+D=0;

2) (4)=>(3) (4) => ал (4) 1 дербес.

Шешімі => (5).

(4)-(5)= (6)

=

(7).

(6)=(7)=>(3) теорема дәлелденді.

Салдары 1. (4) түрлі теңдеу жазықтықтың жалпы теңдеуі д.а.

Салдары 2. (6) теңдеу

( 6) = ( , ) = 0;

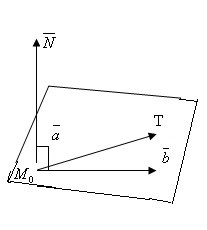
Декарт координаттар жүйесінде (А,В,С) – жазықтықтың нормаль векторы д.а.

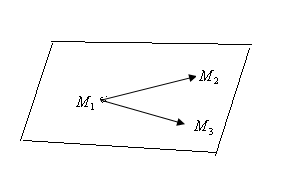
Үш нүкте арқылы жазылған жазықтықтың теңдеуі.

бір түзудің бойында жатпайды.

( 3)

= 0 (8)

Кесінділер арқылы берілген жазықтықтың теңдеуі

( 4) / -D

(9)

= a; = b; = c.

1 ) x=0 y=0 z=c

2 ) x=0 z=0 y=b

3 ) y=0 z=0 x=a

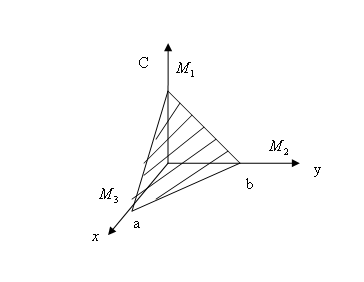
Екі жазықтықтың орналасуы және арасындағы бұрыш.

1 )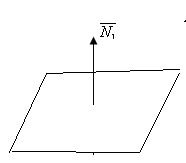

2)

3)

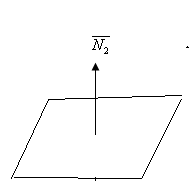
Екі жазықтықтың арасындағы бұрыш –ол нормаль-р-ң арасындағы бұрыш.

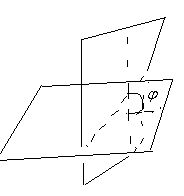
Нүктелердін жазықтыққа дейінгі арақашықтығы.

Ax+By+C+D=0;

d-? (арақашықтық)

M(x,y,z)

d= = = =

8. Эллипс және оның канондық теңдеуі. Эллипстің эксцентриситеті мен

директрисалары.

А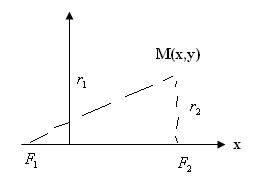 нықтама: Белгіленген 2 нүктеден арақашықтықтарының қосындысы тұрақты болатын жазықтықтағы нүктелер жиыны эллипс д.а.

F1,F2 – нүктелер. 0 координаттар басы F1F2 кесіндісінің ортасы болсын. r1+r2=2a – const

(*)

F₁( -c,0) F₂(c,0) -фокустар д.а.

a-үлкен жарты өсі.

b-кіші жарты өсі.

1)x=0 (0,b) (0, -b)

2)y=0 (a,0) (-a,0)

Эллипстің негізгі тіктөртбұрыш

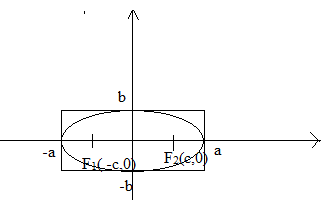
1) a=b

шеңбер эллипстің дербес жағдайы

( кері) Эллипс –шеңберді оу өсімен қосқандағы қисық.

шеңбер

y=

Анықтама: эллипстің саны оның эксцентриситеті деп аталады.

Фокуста жатқан ох осі эллипстің фокалды осі д.а. О(0,0) о-ң центрі болады.

Анықтама:

Эллипстің фокалды осіне перпендикуляр ж/е центрінен а/е арақашықтықта жататын түзулер эллипстің директрисалары д.а.

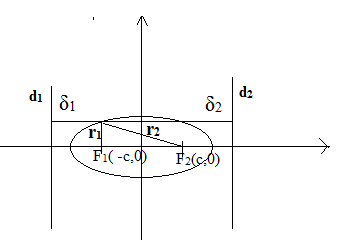
, F₁-ге тиісті директриса

, F₂-ге тиісті директриса

Теорема: Эллипстің кез келген фокусқа дейінгі арақашықтығына сәйкес директрисасына дейінгі арақашықтығына қатынасы е санына тең болады.

кез келген М(х,у)

Д/у:

М(х,у) фокалдық радиустар