
- •2. Дії над матрицями. Властивості дії над матрицями.
- •3. Визначники квадратних матриць Способи обчислення.
- •6. Мінори та алгебраїчні доповнення.
- •4. Визначник n-го порядку Теорема Лапласа
- •5. Визначники. Властивості визначників.
- •7. Обернена матриця. Алгоритм оберненої матриці.
- •8. Ранг матриці Властивості рангу матриці. Елементарні перетворення матриці.
- •Властивості:
- •Елементарні перетворення:
- •9. Основні поняття системи n лінійних алгебраїчних рівнянь з n змінними. Правило Крамера.
- •Правило Крамера
- •10. Матричний метод розв’язання слар
- •11.Теорема Кронекера-Капеллі. Алгоритм розвязування слар
- •12. Метод Гаусса.
- •13. Метод Жорданна-Гаусса.
- •15. Скалярний і векторний добуток. Властивості векторного добутку.
- •16. Мішаний добуток. Властивості мішаного добутку.
- •17. Векторний простір, його розмірність і базис. Розклад вектора за базисом. Лінійно залежні і лінійно незалежні системи векторів.
- •18. Рівняння лінії на площині. Вивести канонічне та параметричне рівняння прямої
- •19. Вивести рівняння прямої, що проходить через дві точки і рівняння прямої у відрізках на осях.
- •20. Векторне рівняння прямої та загальне рівняння прямої і його частинні випадки.
- •21. Нормальне рівняння прямої та рівняння пучка прямих.
- •22. Канонічне рівняння прямої. Умови паралельності та перпендикулярності.
- •23. Рівняння з кутовим коефіцієнтом. Відстань від точки до прямої.
- •24. Кут між прямими, що задані рівнянням з кутом коефіцієнтом. Умови паралельності та перпендикулярності.
- •25. Матриці, основні поняття. Різновиди матриць
- •26.Дії над матрицями. Властивості дій над матрицями
- •27.Визначники квадратних матриць. Способи обчислення визначників
- •28. Визначник n-го порядку. Теорема Лапласа
- •29. Визначники. Властивості визначників
- •30. Мінори та алгебраїчні доповнення
- •31. Різновиди рівняння площини у просторі за 3 точками, у відрізках на осях, нормальне.
- •32. Рівняння площини, що проходить через задану точку перпендикулярно до заданого вектора. Загальне рівняння площини.
- •33. Кут між площинами. Умови паралельності і перпендикулярності двох площин. Відстань від точки до площини.
- •34. Різновиди рівняння прямої в просторі: канонічне, параметричне, за 2 точками. Пряма як перетин двох площин.
- •35. Кут між прямими у просторі. Кут між прямою і площиною. Умови паралельності та перпендикулярності прямої і площини. Знаходження точки перетину прямої і площини.
- •36. Поняття кривих ліній другого порядку. Дослідження рівняння другого порядку. Коло.
- •37. Еліпс: означення, рівняння, графік, вершина, півосі, фокуси, ексцентриситет, директриси.
- •38. Гіпербола.
- •39. Парабола.
- •40. Поняття числової послідовності: формула п-го члена; зростаюча, спадна, обмежена послідовність. Поняття границі числової послідовності.
- •41. Геометрична інтерпретація границі послідовності. Основні властивості границі послідовності.
- •42. Границя функції в точці і на нескінченності: означення, геометрична інтерпретація означення, приклади. Односторонні границі функції в точці.
- •43. Нескінченно малі функції в точні і на нескінченності, означення, властивості, геометрична інтерпретація.
- •45. Теорема про зв’язок між нескінченно малими та великими функціями. Теорема про зв'язок міх нескінченно малою функцією та границею функції.
- •47. Властивості функції, які мають границі в точці: єдність границі, граничний перехід у нерівності, границя проміжної функція, обмеженість функції в точці.
- •48. Властивості границь функції:границя сталої, суми, добутку, частки функцій, границя степеневої функції.
- •49. Розкриття невизначеного вигляду , ,(∞-∞)
- •50. Перша та друга границі та наслідки з них.
- •51. Неперервність функції в точці: означення Коші та означення в термінах приростів функції та аргументу. Застосування поняття неперервності при обчисленні границь функції.
- •52. Властивості функцій у точці. Теорема про неперервність елементарних функцій.
- •53. Властивості функцій неперервних на відрізку. Геометрична інтерпретація цих властивостей.
- •54. Точки розриву функції.
- •55. Задачі, що приводять до поняття похідної.
- •56. Означення похідної. Диференційованість та неперервність функцій в точці і на проміжку.
- •57. Правила диференціювання функцій.
- •59. Геометричний зміст похідної. Рівняння дотичної. Поняття нормалі до графіка функції та її рівняння. Економічний зміст похідної.
- •60. Похідна складної і оберненої функції
- •61 Диференціювання параметрично заданих функцій
- •62 Диференціювання неявно заданих функцій
- •63 Похідна степенево-показннкових функцій
- •64. Похідні внщнх порядків
- •65 Диференціал та його властивості
- •66 Застосування диференціала до наближених обчислень
- •67 Правило Лапіталя
- •68 Застосування правила Лапіталя у невизначеностях виду
- •69 Необхідна й достатня ознака зростання (спадання) функції
- •70 Екстремум функції необхідна та достатня умова існування екстремуму
- •71 Опуклість, вгнутість, точкн перегину
- •72. Опуклість, вгнутість, точкн перегину
- •73.Асимптоти графіка функції
- •74 Функції кілької змінних. Основні поняття
- •75 Функції двох змінних. Область визначення. Лінії рівня
- •76. Лінії рівня функції двох змінних.
- •77.Частиний приріст і частині похідні першого порядку
- •81. Градієнт
- •82. Похідні вищих порядків
- •83. Алгоритм дослідження функції на екстремум за допомогою першої похідної
- •84. Алгоритм дослідження на опуклість і вгнутість
- •85. Загальна схема побудови графыка ф-ї за допомогою похідної
- •86. Правило Лопіталя
- •87. Екстремум ф-ї, необхідна та достатня умови існування екстремуму
- •88. Частинний приріс і частинні похідні першого порядку
- •94. Знаходження екстремуму функції від багатьох змінних
- •95. Знаходження умовного екстремуму.
- •96. Знаходження найбільшого і найменшого значення ф-ї в оласті d
- •97. Поняття первісної
- •98. Невизначений інтеграл.
- •99. Метод безпосереднього інтегрування
- •100. Інтегрування підстановкою ( метод заміни змінної)
- •101.Інтегрування частинами
- •102.Інтегрування виразів, що містять у знаменнику квадратний тричлен
- •103.Інтегрування виразів, що містять у знаменнику квадратний тричлен
- •104 .Метод невизначених коефіцієнтів
- •105.Інтегрування функцій, що містять ірраціональності.
- •106.Інтегрування тригонометричних функцій
- •107.Інтегрування найпростіших раціональних дробів.
- •108.Інтегрування найпростіших раціональних дробів
- •109.Визначений інтеграл та його властивості.
- •110.Задача, що призводить до поняття визначеного інтеграла
- •111.Формула Ньютона –Лейбніца, для обчислення визначених інтегралів.
- •112. Метод безпосереднього інтегрування визначених інтегралів
- •113.Метод інтегрування заміни змінної у визначеному інтегралі.
- •114.Метод інтегрування частинами у визначеному інтегралі.
- •115.Застосування визначеного інтеграла для обчислення площ фігур обмежених лініями.
- •120. Метод найменших квадратів.
- •121. Поняття ряду. Збіжність ряду та його сума.
- •122.Властивості збіжних рядів.
- •123. Необхідна ознака збіжності ряду.
- •124.Еталонні ряди
- •131.Абсолютна та умовна збіжність рядів.
- •132. Функціональні ряди. Основні поняття.
- •133.Степеневі ряди. Основні поняття. Теорема Абеля.
- •134. Радіус, інтервал, область збіжності ряду.
- •135. Ряд Тейлора.
- •136. Ряд Маклорена
- •137. Використання рядів до наближених обчислень функції
- •138. . Використання рядів до наближених обчислень функцій.
- •139. Диференціальні рівняння. Основні поняття та означення
- •140.Диференціальні рівняння першого порядку.Основні поняття.
- •141.Диференціальні рівняння з відокремлюваними змінними.
- •142.Задачі Коші.
- •143.Однорідні диференціальні рівняння першого порядку.
- •144.Лінійні диференціальні рівняння першого порядку.
- •145.Диференціальні рівняння другого порядку. Основні поняття.
- •146. Диференціальні рівняння другого порядку,що допускають пониження порядку.
- •147.Рівняння Бернулі.
- •150.Метод невизначених коефіцієнтів при розв’язуванні лінійних неоднорідних диференціальних рівнянь другого порядку.
106.Інтегрування тригонометричних функцій
Для
інтегрування виразів
 ;
;
 ;
;
зручно користуватися наступними
формулами , які перетворюють добуток
функцій у суму.
;
;
зручно користуватися наступними
формулами , які перетворюють добуток
функцій у суму.
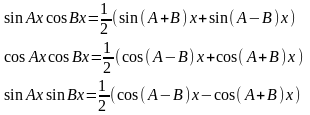
107.Інтегрування найпростіших раціональних дробів.
Означення. Найпростішими раціональними дробами І, ІІ, ІІІ, ІV типу називаються правильні дроби вигляду:

 К≥2,
ціле)
К≥2,
ціле)
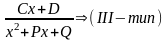 D<0
D<0
 k≥2,
ціле, D<0
k≥2,
ціле, D<0
Розглянемо інтегрування найпростіших раціональних дробів І –ІІ типів




При інтегруванні найпростішого дробу ІV типу потрібно спочатку виділити в знаменнику повний квадрат, а потім вираз, що стоїть під квадратом, замінити на нову змінну. Отже одержимо формулу
 =
=
 ln|x2+2px+q|+
ln|x2+2px+q|+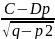 arcctg(
arcctg( +C
+C
108.Інтегрування найпростіших раціональних дробів
Раціональним
дробом називають виразR(x)=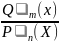 ,
де Qm(x),
Pn(x)-многочлени
відповідних степенів.Якщо m>n,то
дріб неправильний; якщо m<n,то
дріб правильний..
,
де Qm(x),
Pn(x)-многочлени
відповідних степенів.Якщо m>n,то
дріб неправильний; якщо m<n,то
дріб правильний..
Теорема: Будь-який неправильний раціональний дріб розкладається на суму найпростіших раціональних дробів типу І-ІV,коефіцієнти яких можна знайти методом невизначених коефіцієнтів.
1) Корені знаменника дійсні та різні:
Q(x)=(x-1)(x-2)…(x-n)
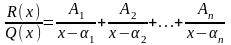
2) Корені дійсні, деякі кратні.


3) Корені дійсні, серед них є кратні, знаменник містить квадратний тричлен.

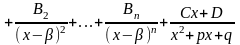
109.Визначений інтеграл та його властивості.
Нехай
— деяка функція, що задана на проміжку
[a;
b].
Розіб’ємо
[a;
b]
на
n
частин точками
 так що
так що

Означення.
Якщо існує скінченна границя інтегральних
сум Sn
при
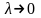 і не залежить ні від способу розбиття
[a;
b]
на частини
і не залежить ні від способу розбиття
[a;
b]
на частини
 ,
ні від вибору точок
,
ні від вибору точок
 ,
то ця границя називається визначеним
інтегралом від функції
на
проміжку [a;
b]
і позначається:
,
то ця границя називається визначеним
інтегралом від функції
на
проміжку [a;
b]
і позначається:
 ,
,
Властивості визначеного інтеграла
І.
Якщо
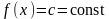 ,
то
,
то

ІІ.
Сталий множник можна виносити з-під
знака визначеного інтеграла, тобто

ІІІ.
Якщо
 та
та
 інтегровні на [a;
b],
то
інтегровні на [a;
b],
то

IV.
Якщо у визначеному інтегралі поміняти
місцями межі інтегрування, то інтеграл
змінить лише свій знак на протилежний,
тобто

V.
Визначений інтеграл з однаковими межами
інтегрування дорівнює нулю
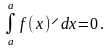
VI.
Якщо
— інтегровна в будь-якому із проміжків:
[a;
b],
[a; c],
[с;
b],
то

VII. Якщо
 і інтегровна для
і інтегровна для
 то
то
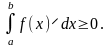
VIII.
Якщо
,
 —
інтегровні та
—
інтегровні та
 для
для

 то
то
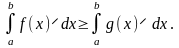
IX. Якщо
f(x)
— інтегровна та
 для
для

 то
то

110.Задача, що призводить до поняття визначеного інтеграла
Задача про площу криволінійної трапеції
Фігуру, обмежену лініями у=f(x), x=a,x=b, y=o,називають криволінійною трапецією. Для обчислення площі криволінійної трапеції поділимо відрізок[a;в] на n частин так, щоб а=х0<x1 <xk …<Xn
Довжини
цих частин позначимо
к= к
-
к-1Перпендикуляри
до осі ОХ проведені з точок поділу до
перетину з кривою у=f(x),
розрізняють усю площу на n-вузькі
криволінійні трапеції. Замінимо кожну
з цих трапецій прямокутником з
прямокутником з основою
к
та
висотою f(ck)
к.Cума
площ усіх прямокутників S=
к
-
к-1Перпендикуляри
до осі ОХ проведені з точок поділу до
перетину з кривою у=f(x),
розрізняють усю площу на n-вузькі
криволінійні трапеції. Замінимо кожну
з цих трапецій прямокутником з
прямокутником з основою
к
та
висотою f(ck)
к.Cума
площ усіх прямокутників S= .
Площа криволінійної трапеції S=
.
значення буде найточніше, якщо перейти
до границі.
.
Площа криволінійної трапеції S=
.
значення буде найточніше, якщо перейти
до границі.
