88. Частинний приріс і частинні похідні першого порядку

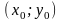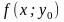Нехай функція визначена в деякому околі точки . При фіксованому дістанемо функцію , яка залежить тільки від однієї змінної х, а при дістанемо функцію , яка залежить тільки від у. Похідна функції при називається частинною похідною по х функції у точці і позначається

,а похідна функції при називається частинною похідною по у функції у точці і позначається .

Різниця 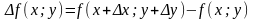називається повним приростом функції , а різниці

називаються частинними приростами функції по х і по у відповідно.

89. Градієнт функції.

Вектор з координатами , який характеризує напрям максимального зростання функції 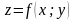у точці , називається градієнтом функції у цій точці і позначається ( — одиничні орти):

Похідна за напрямом 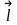функції та градієнт пов’язані співвідношенням

90. .Частинні похідні вищих порядків. Теорема про рівність мішених похідних.

Частинну похідну першого 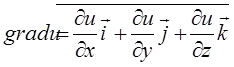порядку по змінній від частинної похідної першого порядку по змінній називають частинною похідною другого порядку функції по змінній та і позначають:

п 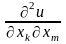при , при k = m.

Теорема. Якщо функція z = f (x;y) та похідні неперервні в точці (х;у) та в деякому її околі, то в цій точці .

91. Похідна за напрямом вектора та градієнт функції

Якщо існує границя відношення при .то цю границю називають похідною функції u(x;y;z) в точці M(x;y;z) за напрямом вектора 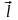і позначають , тобто

. Виведемо формулу для обчислення похідної за напрямом . припустимо , що функція u(x;y;z) диференційована в точці M. Тоді її повний приріст в цій точці можна записати так:

де - нескінченно малі функції при .

Оскільки

То

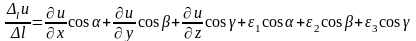
Перейшовши до границі при ,дістанемо формулу для обчислення похідної за напрямом

Вектор, який вказує напрям найшвидшого зростання ф-ції z=f(x;y),називають градієнтом gradz = (ƌu/ƌx; ƌu/ƌy ). Модуль градієнта | grad u | = 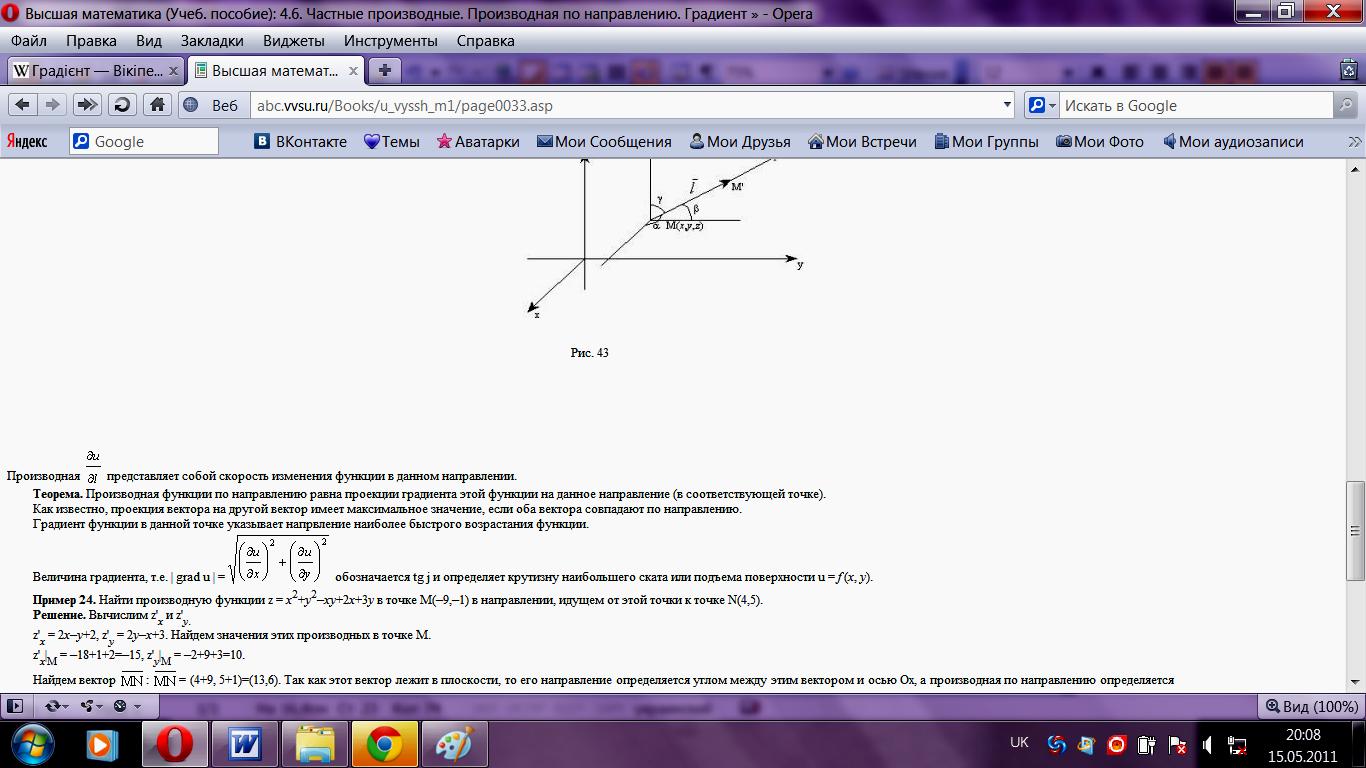визначає швидкість зростання ф-ції. Для ф-ції u=(x,y,z) градієнт знаходять за ф-лою:

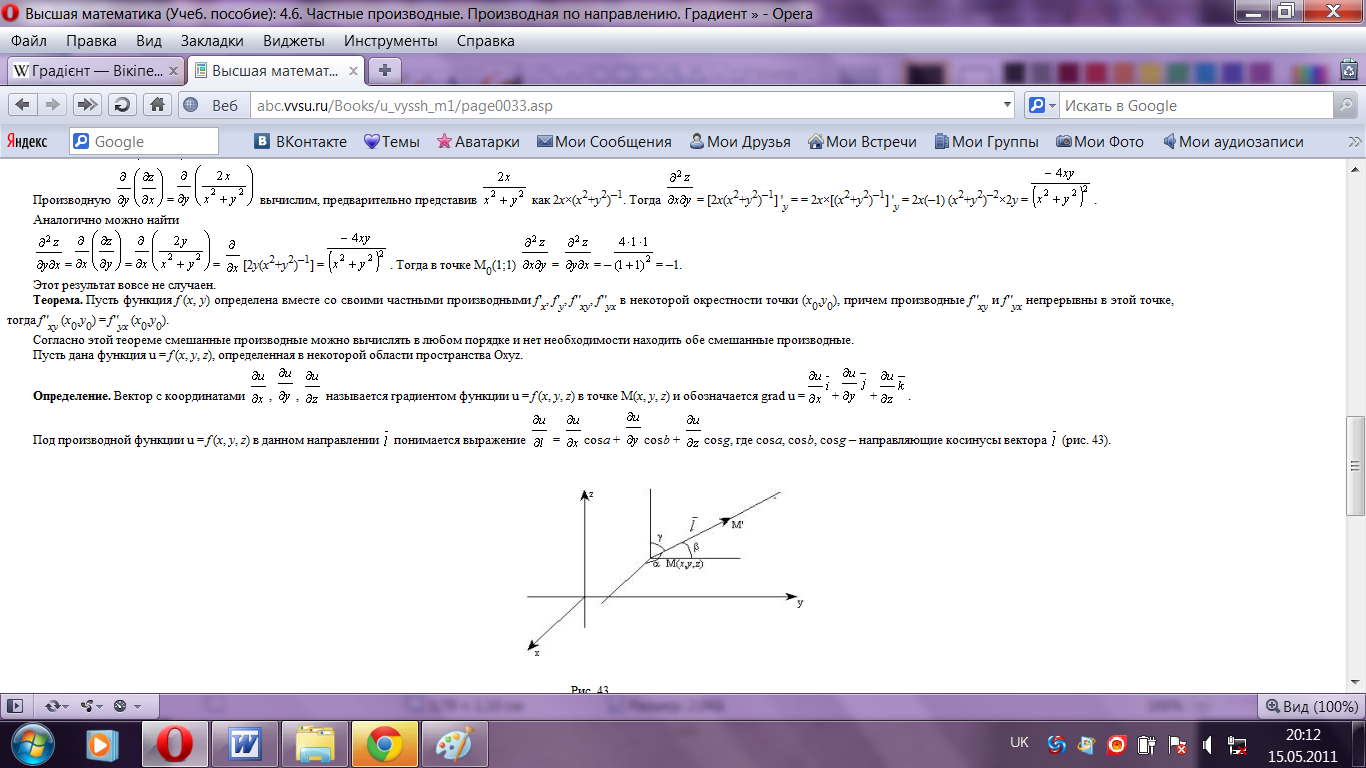
92. -91

93. Застосування диференціалу для наближених обрахунків.

2.Знайти наближене значення .

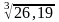Розвязок. У даному випадку

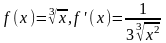
Вважаючи х=27, _х=-0,81 і застосовуючи формулу (3) отримуємо

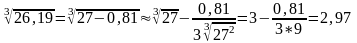
3.Обчислити sin 29⁰ .

Найближчим значенням аргументу, для якого легко визначити значення функції х=30⁰, . Тому згідно формули (3) маємо .

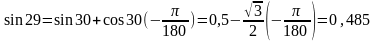94. Знаходження екстремуму функції від багатьох змінних

Означення: Нехай ф-ія z=f(x;y) визначена в деякому околі точки (x₀;y₀) і неперервна в цій точці. Якщо для всіх точок (x;y) цього околу виконується нерівність , тоді ця точка (x₀;y₀) називається точкою максимуму (мінімуму) ф-ії z=f(x;y).

Точки максимуму і мінімуму наз. точками екстремуму.

Теорема (необхідна умова екстремуму): Якщо ф-ія z=f(x;y) має екстремум в точці (x₀;y₀), тоді в цій точці частинні похідні і або дорівнюють нулю, або хоча б одна з них не існує.

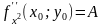
Теорема (достатня умова екстремуму): Нехай ф-ія має екстремум у точці (x₀;y₀), неперервні частинні похідні першого і другого порядку, причому та а також . Якщо:

1. AC-B²>0 і A<0 тоді (x₀;y₀) точка максимуму

2. AC-B²>0 і A>0 тоді точка мінімуму

3. AC-B²<0 екстремуму немає

4. AC-B²=0