Гидродинамика негіздері.

Гидродинамика – сұйықтың қозғалысының заңдылықтары мен оның қозғалысты және қозғалыссыз беттермен әсерлесуін зерттейтін гидравликаның бөлімі.

Егер беріктігі жоғары дененің бөлек бөлшектері өзара берік байланысқан болса, қозғалыстағы сұйық ортада мұндай байланыстар болмайды. Сұйықтың қозғалысы бөлек молекулалардың аса қиын орын ауыстыруы нәтижесінде орындалады.

1. Сұйықтық қозғалысы жайлы негізгі түсінік

Қимыл қима ω (м³) – деп, ағыс бағытына перпенағынның көлденең қимасының ауданын айтамыз. Мысалы, құбырдың қимыл қимасы – шеңбер (3,1 а сурет), кланпанның қимыл қимасы – ішкі диаметрі өзгеретін сақина (3,1 б сурет).

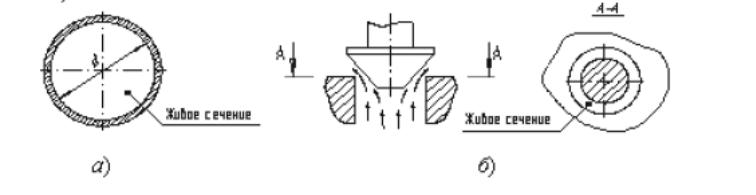
3,1 Сурет. Қимыл қималар: а – құбырдың, б – клапанның.

Суланған периметр χ («хи») – қимыл қима периметрінің берік қабырғалармен шектелген бөлігі (3,2 сурет. Қалың сызық арқылы көрсетілген).

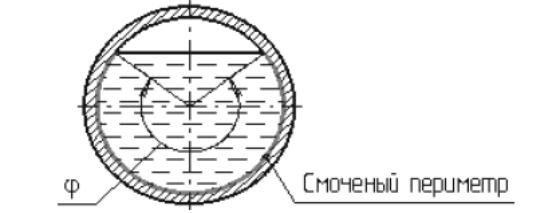
3,2 Сурет. Суланған периметр

Дөңгелек құбыр үшін

егер бұрыш мәні радианмен берілсе,

егер φ бұрыш мәні градуспен берілсе.

Ағыс шығыны Q - қимыл қима ω арқылы t уақыт бірлігінде ағып өтетін сұйық көлемі V.

Ағыстың орташа жылдамдығы υ - сұйықтық шығынының Q қимыл қима ω ауданына қатынасымен анықталатын сұйықтың жылдамдығы.

Сұйықтықтың түрлі бөлшектерінің қозғалыс жылдамдықтары бір-бірінен өзгеше болғандықтан, ағыс жылдамдығы орташаланады. Мысалы, дөңгелек құбырда құбыр осіндегі жылдамдық максимал мәнде, ал құбырдың қабырғалары маңында нөлге тең.

Ағыстың гидравликалық радиусы R – қимыл қиманың суланған периметрге қатынасы.

Сұйықтықтың ағысы орнатылған және орнатылмаған болып келеді. Орнатылған ағыс – деп ағыс арнасының берілген нүктесінде қысым мен жылдамдық уақыт аралығында өзгермейтін сұйықтық ағысын айтады.

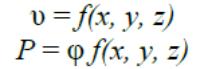
Ал орнатылмаған (тұрақсыз) ағыс – сұйықтықтың ағыс жылдамдығы мен қысымы тек кеңістік координаттарына ғана емес, уақытқа да тәуелді өзгеріп отыратын ағыс.

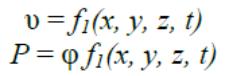
Ток сызығы – (орнатылмаған қозғалыс кезінде қолданылады) әр нүктесінде жылдамдық векторы осы уақытта түйістірілуге бағытталған қисық.

Ток түтігі – шексіз кішігірім көлденең қималы ток сызықтарынан пайда болатын түтікті бет. Ток түтігі ішінде бекітілген ағыс бөлігі элементар ағыс деп аталады.

3,3 Сурет. Ағыс және ток сызығы.

Сұйықтың ағысы арынды және арынсыз болады. Арынды ағыс бос кеңістігі жоқ жабық арнада байқалады. Арынды ағыс жоғары қысымды құбырөткізгіштерде байқалады. Арынсыз ағыс – ашық арналарда (өзендер, ашық каналдар, астаулар және т.с.с.) байқалатын, бос кеңістікті ағыс.берілген бағамда тек арынды ағысты қарастырамыз.

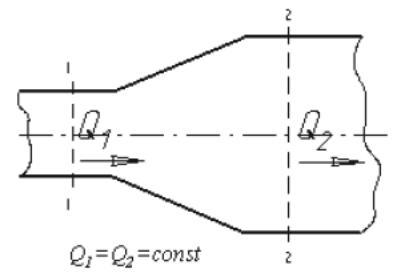
3,4 Сурет. Тұрақты шығындағы ауыспалы диаметрлі құбыр.

Заттың сақталу заңдылығы мен шығын тұрақтылығынан ағыстың үздіксіздік теңдеуі шығады. Ауыспалы қимыл қимасы бар құбырды алайық (3,4 сурет). Құбырдағы сұйық шығыны кез-келген қимасында тұрақты, яғни Q₁ = Q₂ = const, бұдан

Осылайша, егер құбыр ішіндегі ағыс үздіксіз әрі тұтас болса, онда үздіксіздік теңдеуі келесі түрге ие болады:

2. Идеал сұйық үшін Бернулли теңдеуі.

1738 жылы шыққан Даниила Бернуллидің теңдеуі – гидродинамиканың негізгі теңдеуі болып табылады. Бұл теңдеу ағыстың түрлі қималарында Р қысым мен υ орташа жылдамдық және z пьезометрлік биіктік араларындағы байланысты анықтайды және қозғалыстағы сұйықтықтың энергия сақталу заңын көрсетеді. Осы теңдеу арқылы көптеген есептер шығарылады.

β бұрышы маңындағы кеңістікте ораласқан ауыспалы диаметрлі құбырды қарастырайық (3,5 сурет).

Құбырөткізгіштің қарастырылып отырған аумағынан кез-келген екі қиманы таңдап алайық: 1-1 қимасы және 2-2 қимасы. Шығыны Q ге тең болатын сұйықтық бірінші қимадан екінші қимаға қарай құбырөткізгішбойымен жоғары қозғалуда.

Сұйықтық қысымын өлшеу үшін, сұйықтық деңгейі биіктігіне көтерілетін, қабырғалары жұқа түтікшелер – пьезометрлер қолданылады.

Пьезометрлерден басқа, 1-1 және 2-2 әрбір қимасында бұралған соңы Пито түтікшесі деп аталатын сұйықтық ағысына қарама-қарсы бағытталған түтікше орнатылған. Сол сияқты, егер сұйықтық деңгейлерін пьезометрлік сызықтан бастап есептесе, Пито түтікшесіндегі сұйықтықтар түрлі деңгейлерге көтеріледі.

Пьезометрлік сызықты келесітүрде тұрғызуға болады. Егер 1-1 және 2-2 қималары арасында бірнеше бірдей пьезометр орналастырсақ, және сұйықтық деңгейінің көрсеткіштері арасында олардың бойымен қисық жүргізсек, онда біз сынық сызық аламыз (3,5 сурет).

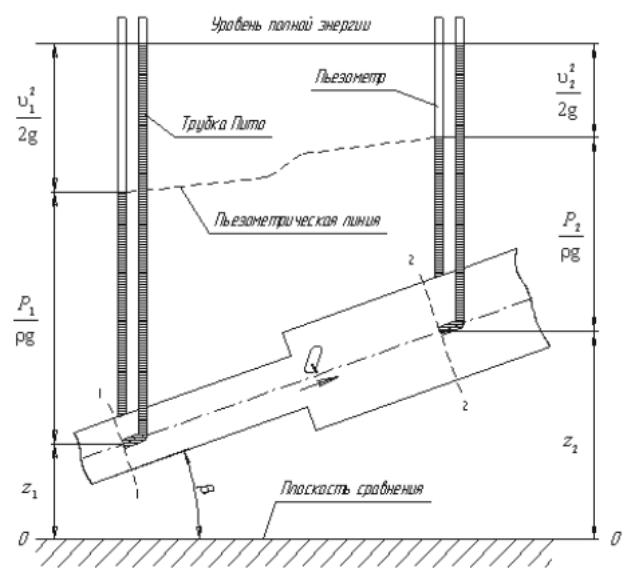
3,5 сурет. Идеал сұйықтыққа арналған Бернулли теңдеуінің қорытындысының сұлбасы.

Алайда, Пито түтікшелерінде салыстыру жазықтығы деп аталатын, 0-0 еркін орналасқан горизонталь түзуіне қатысты биіктік деңгейлері бірдей болады.

Егер Пито түтіешелеріндегі сұйықтық деңгейлеріндегі көрсеткіштер арқылы сызық жүргізсе, ол сызық горизонталь болады және құбырөткізгіштің толық энергиясының деңгейін көрсетеді.

Идеал сұйықтық ағысының екі: 1-1 және 2-2 еркін қималары үшін Бернулли теңдеуі кеелсі түрде болады:

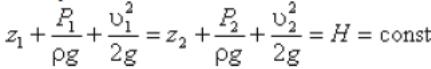
1-1 және 2-2 қималары еркін түрде алынғандықтан, алынған теңдеуді басқа түрде жазуға болады:

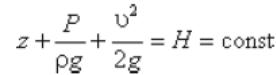
және: идеал сұйықтық ағысының кез-келген қимасы үшін үздіксіз мөлшер - Бернулли теңдеуінің үш мүшесінің суммасына тең.

Энергетикалық тұрғыдан қарағанда, теңдеудің әр мүшесі энергияның белгілі бір түрін білдіреді:

z₁ және z₂ – 1-1 және 2-2 қималарындағы потенциал энергияны сипаттайтын күйдің меншікті энергиялары;

және - сол қималардағы потенциал энергияны сипаттайтын қысымның меншікті энергиялары;

және - сол қималардағы меншікті кинематикалық энергиялар;

Осыдан, Бернулли теңдеуіне сәйкес, идеал сұйықтықтың толық меншікті энергиясы кез-келген қимада тұрақты.

Бернулли теңдеуін геометрия тілінде де түсіндіруге болады. Мәселе теңдеудің әр мүшесінің өзінің сызықтық өлшемінің болуында. 3,5 суретке қарап отырып, z₁ және z₂ – салыстыру жазықтығындағы 1-1 және 2-2 қималарының геометриялық биіктіктері; және - аталған қималардың пьезометрлік биіктіктері; ал және - аталған қималардың жылдамдық биіктіктері екендігін аңғарамыз.

Бұл жағдайда Бернулли теңдеуін: идеал сұйықтық үшін үздіксіз мөлшер – геометриялық, пьезометрлік және жылдамдық биіктіктерінің суммасына тең – деп оқи аламыз.