Третий закон Ньютона
Этот закон объясняет, что происходит с
двумя взаимодействующими телами. Возьмём
для примера замкнутую систему, состоящую
из двух тел. Первое тело может действовать
на второе с некоторой силой
,
а второе — на первое с силой
.
Как соотносятся силы? Третий закон
Ньютона утверждает: сила действия равна
по модулю и противоположна по направлению
силе противодействия. Подчеркнём, что
эти силы приложены к разным телам, а
потому вовсе не компенсируются.
Сам закон:
-
Тела попарно действуют друг на друга с силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей центры масс этих тел, равными по модулю и противоположными по направлению:
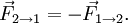
Историческая формулировка
-
Действию всегда есть равное и противоположное противодействие, иначе — взаимодействия двух тел друг на друга равны и направлены в противоположные стороны.
Выводы
Из законов Ньютона сразу же следуют некоторые интересные выводы. Так, третий закон Ньютона говорит, что, как бы тела ни взаимодействовали, они не могут изменить свой суммарный импульс: возникает закон сохранения импульса. Далее, если потребовать, чтобы потенциал взаимодействия двух тел зависел только от модуля разности координат этих тел U( | r1 − r2 | ), то возникает закон сохранения суммарной механической энергии взаимодействующих тел:
Законы Ньютона являются основными законами механики. Из них могут быть выведены уравнения движения механических систем. Однако не все законы механики можно вывести из законов Ньютона. Например, закон всемирного тяготения или закон Гука не являются следствиями трёх законов Ньютона.
Третий закон Ньютона
Для любых двух тел (назовем их тело 1 и тело 2) третий закон Ньютона утверждает, что любая сила, которая обусловлена действием тела 1 на тело 2, сопровождается появлением равной по модулю, но противоположной по направлению силы, действующей на тело 2 со стороны тела 1.[11] Математически закон записывается так:
Этот закон означает, что силы всегда возникают парами «действие-противодействие».[8] Если тело 1 и тело 2 находятся в одной системе, то суммарная сила в системе, обусловленная взаимодействием этих тел равна нулю:
Это означает, что в замкнутой системе не существует несбалансированных внутренних сил. Это приводит к тому, что центр масс замкнутой системы (то есть той, на которую не действуют внешние силы) не может двигаться с ускорением. Отдельные части системы могут ускоряться, но лишь таким образом, что система в целом остается в состоянии покоя или равномерного прямолинейного движения. Однако в том случае, если внешние силы подействуют на систему, то ее центр масс начнет двигаться с ускорением, пропорциональным внешней результирующей силе и обратно пропорциональным массе системы.
Во всех явлениях природы сила, независимо от своего происхождения, проявляется только в механическом смысле, т.е. как причина нарушения равномерного и прямолинейного движения тела в инерциальной системе координат.Обратное утверждение, т.е установление факта такого движения, не свидетельствует об отсутствии действующих на тело сил, а лишь о том, что действия этих эти сил взаимно уравновешиваются. Иначе: их векторная сумма есть вектор с модулем, равным нулю.На этом основано измерение величины силы, когда она компенсируется силой, величина которой известна .
Второй закон Ньютона позволяет измерять величину силы. Например, знание массы планеты и ее центростремительного ускорения при движении по орбите позволяет вычислить величину силы гравитационного притяжения, действующую на эту планету со стороны Солнца.
Силы трения скольжения — силы, возникающие между соприкасающимися телами при их относительном движении. Если между телами отсутствует жидкая или газообразная прослойка (смазка), то такое трение называется сухим. В противном случае, трение называется «жидким». Характерной отличительной чертой сухого трения является наличие трения покоя.
Опытным путём установлено, что сила трения зависит от силы давления тел друг на друга (силы реакции опоры), от материалов трущихся поверхностей, от скорости относительного движения и не зависит от площади соприкосновения. (Это можно объяснить тем, что никакое тело не является абсолютно ровным. Поэтому истинная площадь соприкосновения гораздо меньше наблюдаемой. Кроме того, увеличивая площадь, мы уменьшаем удельное давление тел друг на друга.) Величина, характеризующая трущиеся поверхности, называется коэффициентом трения, и обозначается чаще всего латинской буквой «k» или греческой буквой «μ». Она зависит от природы и качества обработки трущихся поверхностей. Кроме того, коэффициент трения зависит от скорости. Впрочем, чаще всего эта зависимость выражена слабо, и если большая точность измерений не требуется, то к можно считать постоянным.
В первом приближении величина силы трения скольжения может быть рассчитана по формуле:
,
где
—
коэффициент
трения скольжения,
—
сила
нормальной реакции опоры.
По физике взаимодействия трение принято разделять на:
Сухое, когда взаимодействующие твёрдые тела не разделены никакими дополнительными слоями/смазками — очень редко встречающийся на практике случай. Характерная отличительная черта сухого трения — наличие значительной силы трения покоя.
Сухое с сухой смазкой (графитовым порошком)
Жидкостное, при взаимодействии тел, разделённых слоем жидкости или газа (смазки) различной толщины — как правило, встречается при трении качения, когда твёрдые тела погружены в жидкость;
Смешанное, когда область контакта содержит участки сухого и жидкостного трения;
Граничное, когда в области контакта могут содержатся слои и участки различной природы (окисные плёнки, жидкость и т. д.) — наиболее распространённый случай при трении скольжения.
В связи со сложностью физико-химических процессов, протекающих в зоне фрикционного взаимодействия, процессы трения принципиально не поддаются описанию с помощью методов классической механики.
При механических процессах всегда происходит в большей или меньшей степени преобразование механического движения в другие формы движения материи (чаще всего в тепловую форму движения). В последнем случае взаимодействия между телами носят названия сил трения.
Опыты с движением различных соприкасающихся тел (твёрдых по твёрдым, твёрдых в жидкости или газе, жидких в газе и т. п.) с различным состоянием поверхностей соприкосновения показывают, что силы трения проявляются при относительном перемещении соприкасающихся тел и направлены против вектора относительной скорости тангенциально к поверхности соприкосновения. При этом всегда происходит нагревание взаимодействующих тел.
Силами трения называются тангенциальные взаимодействия между соприкасающимися телами, возникающие при их относительном перемещении. Силы трения возникающие при относительном перемещении различных тел, называются силами внешнего трения.
Силы трения возникают и при относительном перемещении частей одного и того же тела. Трение между слоями одного и того же тела называется внутренним трением.
В реальных движениях всегда возникают силы трения большей или меньшей величины. Поэтому при составлении уравнений движения, строго говоря, мы должны в число действующих на тело сил всегда вводить силу трения F тр.
Тело движется равномерно и прямолинейно, когда внешняя сила уравновешивает возникающую при движении силу трения.
Для измерения силы трения, действующей на тело, достаточно измерить силу, которую необходимо приложить к телу, чтобы оно двигалось без ускорения.
Вя́зкость (вну́треннее тре́ние) — одно из трёх явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. Механизм внутреннего трения в жидкостях и газах заключается в том, что хаотически движущиеся молекулы переносят импульс из одного слоя в другой, что приводит к выравниванию скоростей — это описывается введением силы трения. Вязкость твёрдых тел обладает рядом специфических особенностей и рассматривается обычно отдельно.
Различают динамическую вязкость (единицы измерения: пуаз, 0,1Па·с) и кинематическую вязкость (единицы измерения: стокс, м²/с, внесистемная единица — градус Энглера). Кинематическая вязкость может быть получена как отношение динамической вязкости к плотности вещества и своим происхождением обязана классическим методам измерения вязкости, таким как измерение времени вытекания заданного объёма через калиброванное отверстие под действием силы тяжести.
Прибор
для измерения вязкости называется
вискозиметром.
Вязкость газов
В кинетической теории газов коэффициент внутреннего трения вычисляется по формуле
,
где
—
средняя скорость теплового движения
молекул, λ − средняя длина свободного
пробега.
Вторая вязкость
Вторая вязкость — внутреннее трение при переносе импульса в направлении движения. Влияет только при учёте сжимаемости и/или при учёте неоднородности коэффициента второй вязкости по пространству.
Если динамическая (и кинематическая) вязкость характеризует деформацию чистого сдвига, то вторая вязкость характеризует деформацию объёмного сжатия.
Вязкость жидкостей
Внутреннее трение жидкостей, как и газов, возникает при движении жидкости вследствие переноса импульса в направлении, перпендикулярном к направлению движения. Справедлив общий закон внутреннего трения — закон Ньютона:
Коэффициент вязкости η (динамическая вязкость) может быть получен на основе соображений о движениях молекул. Очевидно, что η будет тем меньше, чем меньше время t «оседлости» молекул. Эти соображения приводят к выражению для коэффициента вязкости, называемому уравнением Френкеля-Андраде:
η = Cew / kT
Иная формула, представляющая коэффициент вязкости, была предложена Бачинским. Как показано, коэффициент вязкости определяется межмолекулярными силами, зависящими от среднего расстояния между молекулами; последнее определяется молярным объёмом вещества VM. Многочисленные эксперименты показали, что между молярным объёмом и коэффициентом вязкости существует соотношение
где с и b — константы. Это эмпирическое соотношение называется формулой Бачинского.