Обобщённый импульс в аналитической механике

В теоретической механике обобщённым импульсом называется частная производная лагранжиана системы по обобщённой скорости . В случае, если лагранжиан системы не зависит от некоторой обобщённой координаты, то в силу уравнений Лагранжа .

Для свободной частицы функция Лагранжа имеет вид: , отсюда:

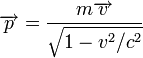
Независимость лагранжиана замкнутой системы от её положения в пространстве следует из свойства однородности пространства: для хорошо изолированной системы её поведение не зависит от того, в какое место пространства мы её поместим. По теореме Нётер из этой однородности следует сохранение некоторой физической величины. Эту величину и называют импульсом (обычным, не обобщённым).

Формальное определение импульса

Импульсом называется сохраняющаяся физическая величина, связанная с однородностью пространства (инвариант относительно трансляций).

Импульс в квантовой механике Формальное определение

В квантовой механике импульсом частицы называют оператор — генератор группы трансляций. Это эрмитов оператор, собственные значения которого отождествляются с импульсом системы частиц. В координатном представлении для системы нерелятивистских частиц он имеет вид

где  — оператор набла, соответствующий дифференцированию по координатам j-ой частицы. Гамильтониан системы выражается через оператор импульса:

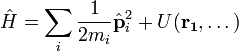
Для замкнутой системы (U = 0) оператор импульса коммутирует с гамильтонианом и импульс сохраняется.

Определение через волны де Бройля

Этот раздел не завершён. Вы поможете проекту, исправив и дополнив его.

Формула де Бройля связывает импульс и длину волны де Бройля.

Модуль импульса обратно пропорционален длине волны λ:

В векторном виде это записывается как где — волновой вектор, h — постоянная Планка.

Импульс - векторная величина , имеет такое же направление , что и скорость . Единица импульса в системе СИ = 1 кг • 1 м/c .

(*)

Изменение импульса материальной точки пропорционально приложенной к ней силе и имеет такое же направление , как и сила . Именно так был впервые сформулирован второй закон Ньютона . Произведение силы на время её действия называют импульсом силы . Так же следует знать , что импульс системы материальных точек равен векторной сумме всех точек .

Заключение

И так сегодня мы узнали , что такое импульс материальной точки и масса . А также получили представление второго закона Ньютона в двух вариантах , их нужно запомнить , и в первую очередь понимать смысл всех величин , входящих в этот закон .

Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между равнодействующей всех приложенных к телу сил и ускорением этого тела. Один из трёх законов Ньютона.

Второй закон Ньютона утверждает: в инерциальных системах ускорение приобретаемое материальной точкой (телом) прямо пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела).

Этот закон записывается в виде формулы:

где — ускорение тела (вектор), — сила, приложенная к телу (вектор), а m — масса тела.

Или, в более известном виде:

в тех же обозначениях.

В случае, если масса тела меняется со временем, то второй закон Ньютона записывается в общем виде (в таком виде его написал сам Ньютон):

где p — импульс (количество движения) тела, t — время, а d/dt — производная по времени.

Второй закон Ньютона справедлив только для скоростей, много меньших скорости света и в инерциальных системах отсчёта.