Равнодействующая

Равнодействующая сила - геометрическая сумма всех сил, действующих на тело. При этом действие каждой силы не зависит от действия других, т.е. каждая сила сообщает телу такое ускорение, какое она сообщила бы в отсутствие действия других сил.Это утверждение носит название принципа независимости действия сил.

При расчёте ускорения тела все действующие на него силы заменяют одной силой, называемой равнодействующей

Понятие массы

У скорение тела определяется действующей на него силой . Но оно зависит и от свойств самого тела . Характер этой зависимости установил Второй Закон Ньютона , с ним мы и познакомимся . Опыты говорят нам о том , что ускорение тела зависит не только от оказываемого на него воздействия , ( т . е . силы ) но и от свойств самого тела менять свою скорость под влиянием определённой силы . Чем больше масса тела , тем меньше получаемое телом ускорение при действии на него заданной силы . Величину , равную отношению модуля силы к модулю ускорения , называют массой ( точнее , инертной массой ) тела . Масса - основная динамическая характеристика тела , количественная мера его инертности , т . е . способности тела приобретать определённое ускорение под действием силы . Для данного тела ускорение пропорционально силе , и коэффициентом пропорциональности является масса . Единица массы в СИ - 1 Кг .

В этом уравнении появилась новая физическая величина – импульс материальной точки . Импульсом материальной точки называют величину , равную произведению массы точки на её скорость . Импульс обозначается буквой p .

Импульс (количество движения) — мера механического движения; представляет собой векторную величину, в классической механике равную для материальной точки произведению массы m этой точки на её скорость v и направленную так же, как вектор скорости: .

Существует более общее определение импульса, верное и в релятивистской механике. Импульс (количество движения) — аддитивный интеграл движения механической системы, связанный согласно теореме Нётер с фундаментальной симметрией — однородностью пространства.

История появления термина

Ещё в первой половине XVII века понятие импульса введено Рене Декартом. Так как физическое понятие массы в то время отсутствовало, он определил импульс как произведение «величины тела на скорость его движения». Позже такое определение было уточнено Исааком Ньютоном. Согласно Ньютону, «количество движения есть мера такового, устанавливаемая пропорционально скорости и массе».

«Школьное» определение импульса

В классической механике полным импульсом системы материальных точек называется векторная величина, равная сумме произведений масс материальных точек на их скорости:

(отсюда следует закон сохранения импульса)

соответственно величина называется импульсом одной материальной точки. Это векторная величина, направленная в ту же сторону, что и скорость частицы. Единицей измерения импульса в Международной системе единиц (СИ) является килограмм-метр в секунду (кг·м/с)

Если мы имеем дело с телом конечного размера, для определения его импульса необходимо разбить тело на малые части, которые можно считать материальными точками и просуммировать по ним, в результате получим:

Импульс системы, на которую не действуют никакие внешние силы (или они скомпенсированы), сохраняется во времени:

. (*)

Сохранение импульса в этом случае следует из второго и третьего закона Ньютона: написав второй закон Ньютона для каждой из составляющих систему материальных точек и просуммировав по всем материальным точкам, составляющим систему, в силу третьего закона Ньютона получим равенство (*).

В релятивистской механике трёхмерным импульсом системы невзаимодействующих материальных точек называется величина

,

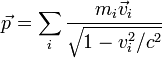где m_i — масса покоя i-й материальной точки.

Для замкнутой системы не взаимодействующих материальных точек эта величина сохраняется. Однако трёхмерный импульс не есть релятивистски инвариантная величина, так как он зависит от системы отсчёта. Более осмысленной величиной будет четырёхмерный импульс, который для одной материальной точки определяется как

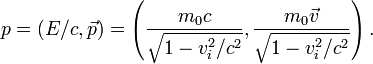
В принципе, для системы невзаимодействующих материальных точек их 4-импульсы суммируются. Однако для взаимодействующих частиц в релятивистской механике следует учитывать импульсы не только составляющих систему частиц, но и импульс поля взаимодействия между ними. Поэтому гораздо более осмысленной величиной в релятивистской механике является тензор энергии-импульса, который в полной мере удовлетворяет законам сохранения.