Работа в термодинамике
В термодинамике работа, совершенная газом (работа совершенная над газом), рассчитывается как интеграл давления по объему:
.
Работа силы в теоретической механике
Работа силы имеет смысл энергии, которая затрачивается источником силы (силовым полем) на своё влияние на процесс γ.
Пусть материальная точка M движется
по непрерывно дифференцируемой кривой
G = {r = r(s)}, где s —
переменная длина дуги,
и на нее действует сила
F(s), направленная по касательной
к траектории в направлении движения.
Величина
,
называется элементарной работой
силы
F на участке Gi и
принимается за приближенное значение
работы, которую производит сила F,
воздействующая на материальную точку,
когда последняя проходит кривую Gi.
Сумма всех элементарных работ
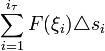является
интегральной суммой Римана функции
F(s).
Определение
Предел, к которому стремится сумма всех элементарных работ, когда мелкость | τ | разбиения τ стремится к нулю, называется работой силы F вдоль кривой G.
Таким образом, если обозначить эту работу буквой W, то, в силу данного определения,
,
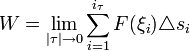следовательно,
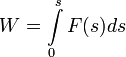(1).
Если положение точки на траектории ее
движения описывается с помощью какого-либо
другого параметра t (например,
времени) и если величина пройденного
пути s = s(t),
является
непрерывно дифференцируемой функцией,
то из формулы (1) получим
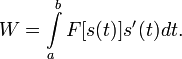
Размерность и единицы
Единицей измерения работы в СИ является Джоуль, в СГС — эрг 1 Дж = кг·м²/с² = Н·м 1 эрг = г·см²/с² = дин·см
1 эрг = 10−7 Дж (точно).
Мощность — физическая величина, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.
-
—
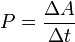средняя мощность
-
—
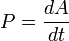мгновенная мощность
Так как работа является мерой изменения энергии, мощность можно определить также как скорость изменения энергии системы. Единицы измерения
В системе СИ единицей измерения мощности является ватт, равный одному джоулю, делённому на секунду.
Другой распространённой единицей измерения мощности является лошадиная сила.
Соотношения между единицами мощности |
|||||||
Единицы |
Вт |
кВт |
МВт |
Н*м/с |
эрг/с |
л. с.(мет.) |
л. с.(анг.) |
1 ватт |
1 |
10-3 |
10-6 |
0,102 |
107 |
1,36·10-3 |
1,34·10-3 |
1 киловатт |
103 |
1 |
10-3 |
102 |
1010 |
1,36 |
1,34 |
1 мегаватт |
106 |
103 |
1 |
102·103 |
1013 |
1,36·103 |
1,34·103 |
1 килограмм-сила-метр в секунду |
9,81 |
9,81·10-3 |
9,81·10-6 |
1 |
9,81·107 |
1,33·10-2 |
1,31·10-2 |
1 эрг в секунду |
10-7 |
10-10 |
10-13 |
1,02·10-8 |
1 |
1,36·10-10 |
1,34·10-10 |
1 лошадиная сила (метрическая) |
735,5 |
735,5·10-3 |
735,5·10-6 |
75 |
7,355·109 |
1 |
0,9863 |
1 лошадиная сила (английская) |
745,7 |
745,7·10-3 |
745,7·10-6 |
76,04 |
7,457·109 |
1,014 |
1 |