Второй закон Кеплера (закон площадей)

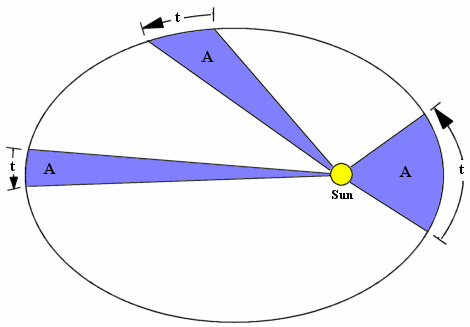
Второй закон Кеплера.

Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные времена радиус-вектор, соединяющий Солнце и планету, заметает сектора равной площади.

Применительно к нашей Солнечной системе, с этим законом связаны два понятия: перигелий — ближайшая к Солнцу точка орбиты, и афелий — наиболее удалённая точка орбиты. Таким образом, из второго закона Кеплера следует, что планета движется вокруг Солнца неравномерно, имея в перигелии большую линейную скорость, чем в афелии.

Каждый год в начале января Земля, проходя через перигелий, движется быстрее, поэтому видимое перемещение Солнца по эклиптике к востоку также происходит быстрее, чем в среднем за год. В начале июля Земля, проходя афелий, движется медленнее, поэтому и перемещение Солнца по эклиптике замедляется. Закон площадей указывает, что сила, управляющая орбитальным движением планет, направлена к Солнцу.

По определению угловой момент точечной частицы с массой m и скоростью записывается в виде:

.

где - радиус-вектор частицы а - импульс частицы.

По определению

.

В результате мы имеем

.

Продифференцируем обе части уравнения по времени

поскольку векторное произведение параллельных векторов равно нулю. Заметим, что F всегда параллелен r, поскольку сила радиальная, и p всегда параллелен v по определению. Таким образом можно утверждать, что - константа.

Третий закон Кеплера (гармонический закон)

Квадраты периодов обращения планет вокруг Солнца относятся, как кубы больших полуосей орбит планет. Справедливо не только для планет,но и для их спутников.

, где T₁ и T₂ — периоды обращения двух планет вокруг Солнца, а a₁ и a₂ — длины больших полуосей их орбит.

Ньютон установил, что гравитационное притяжение планеты определенной массы зависит только от расстояния до неё, а не от других свойств, таких, как состав или температура. Он показал также, что третий закон Кеплера не совсем точен — в действительности в него входит и масса планеты: , где M – масса Солнца, а m₁ и m₂ – массы планет.

Поскольку движение и масса оказались связаны, эту комбинацию гармонического закона Кеплера и закона тяготения Ньютона используют для определения массы планет и спутников, если известны их орбиты и орбитальные периоды.

Механическая работа

Работа силы F за время Δt процесса γ(t)) — это физическая величина, являющаяся количественной характеристикой действия силы F на процесс γ(t), зависящая от численной величины и направления силы и от перемещения точки ее приложения

Работа в механике

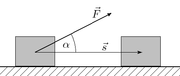
При прямолинейном движении и постоянном значении силы работа равна произведению величины проекции вектора силы на направление движения и величины пройденного пути

При этом действующая сила F и вектор скорости v за всё время наблюдения Δt должны быть постоянны, в противном случае она вычисляется как интеграл:

.

Как следствие, если направление движения тела ортогонально силе F, её работа равна нулю.

Если масса частицы постоянна, а A_total — полная работа, совершённая над частицей, определяемая как сумма работ совершенных приложенными к частице силами, то из второго закона Ньютона можно получить:

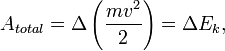
где E_k называется кинетической энергией. Для материальной точки, кинетическая энергия определяется как работа силы, ускорившей точку от нулевой скорости до скорости v:

Для сложных объектов, состоящих из множества частиц, кинетическая энергия тела равна сумме кинетических энергий частиц.

Сила называется потенциальной, если существует скалярная функция, известная как потенциальная энергия и обозначаемая E_p, такая что

Если все силы, действующие на частицу консервативны, и E_p является полной потенциальной энергий, полученной суммированием потенциальных энергий соответствующих каждой силе, тогда:

.

Этот результат известен как сохранение механической энергии и утверждает, что полная механическая энергия в замкнутой системе, в которой действуют консервативные силы

является постоянной относительно времени. Этот закон широко используется при решении задач классической механике.