Движение двух тел в плоскости

Замечательно, что движение двух тел всегда происходит в плоскости. Определим линейный импульс и угловой момент

Скорость изменения углового момента равна моменту силы

однако законы движения Ньютона выполняются для всех физических сил, и гласят, что сила, действующая между двумя частицами (материальными точками) направлена по линии соединяющей их положения, то есть . Отсюда и угловой момент сохраняется. тогда вектор смещения и его скорость лежат в плоскости перпендикулярной постоянному вектору .

Общее решение для силы, зависящей от расстояния

Часто полезно перейти в полярные координаты, поскольку движение происходит в плоскости и для многих физических задач сила является функцией радиуса r (центральные силы). Поскольку r-компонента ускорения равняется , уравнение для r-компоненты вектора смещения можно переписать в виде

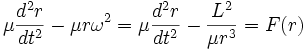
где и угловой момент L = μr²ω сохраняется. сохранение углового момента позволят найти решение для траектории r(θ) используя замену переменных. Переходя от t к θ

получим уравнение движения

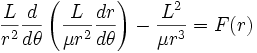
Это уравнение становится квазилинейным при замене переменных и умножение обоих частей уравнения на

Применение

Для сил F обратно пропорциональных квадрату расстояния, таких как гравитация или электростатика в классической физике получим

для некоторых констант α, уравнение для траекторий становится линейным

Решение этого уравнения

где A > 0 и θ₀ константы. Это решение показывает, что орбита представляет собой коническое сечение, то есть эллипс, гиперболу или параболу, в зависимости от того меньше A выражения , больше или равно.

Задача двух тел в ото

Нормальная орбита любого тела, захваченного притяжением другого тела, представляет собой эллипс или окружность – именно такие орбиты мы наблюдаем в Солнечной системе. Однако общая теория относительности утверждает, что в окрестностях крайне массивных тел — там, где пространство оказывается сильно искривлено благодаря наличию колоссального гравитационного поля — спектр возможных стабильных орбит значительно расширяется. В подобных условиях физические объекты начинают вести себя весьма странно. Например, тело может подлететь к черной дыре по крутой параболе, сделать вокруг нее несколько стремительных коротких витков, а затем снова заложить вытянутую петлю – и так далее.

Пример

Любая классическая система состоящая из двух частиц, по определению задача двух тел. Во многих случаях, однако, одно тело много тяжелее другого, как например в системе Земля и Солнце. В таких случаях более тяжёлая частица играет роль центра масс и задача сводится к задаче о движения одного тела в потенциале другого.[1]

Зако́ны Ке́плера — три эмпирических соотношения, интуитивно подобранных Иоганном Кеплером на основе анализа астрономических наблюдений Тихо Браге. Описывают идеализированную гелиоцентрическую орбиту планеты. В рамках классической механики выводятся из решения задачи двух тел предельным переходом m_p/m_S → 0, где m_p, m_S — массы планеты и Солнца.

Первый закон Кеплера (закон эллипсов)

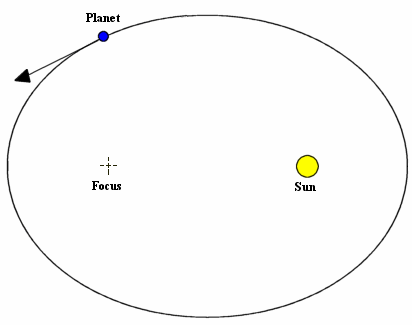
Первый закон Кеплера.

Каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце.

Комментарий: Первый закон Кеплера немедленно противоречит классическому закону сохранения импульса, как только слово «находится» оказывается тождественным слову «покоится». Классическая динамика Ньютона чрезвычайно чувствительна к выбору системы отсчёта, а именно к свойству инерциальная/неинерциальная. В той мере, в которой законы Кеплера претендуют на общность, система отсчёта подразумевается общей — гелиоцентрической. Следовательно, кеплеровское Солнце «покоится» в фокусе каждой эллиптической орбиты (тем самым Кеплер подразумевает разложение Солнечной системы в прямую сумму независимых орбит). Однако суммарный импульс системы p₁+p₂, в которой «тяготеющее» тело покоится p₂=0, равен импульсу единственно подвижного тела p₁. Если последнее изменяется, суммарный импульс — вектор непостоянный. Нижеследующее «доказательство» подразумевает, что центр масс системы «Солнце — планета» совпадает с центром Солнца (на самом же деле для Меркурия несовпадение составляет порядка 10^-7, для Юпитера — 10^-3).

Форма эллипса и степень его сходства с окружностью характеризуется отношением , где c — расстояние от центра эллипса до его фокуса (половина межфокусного расстояния), a — большая полуось. Величина e называется эксцентриситетом эллипса. При c = 0 и e = 0 эллипс превращается в окружность.

Закон всемирного тяготения Ньютона гласит, что «каждый объект во вселенной притягивает каждый другой объект по линии соединяющей центры масс объектов, пропорционально массе каждого объекта, и обратно пропорционально квадрату расстояния между объектами». Это предполагает, что ускорение a имеет форму

Вспомним, что в полярных координатах

В координатной форме запишем

Подставляя и во второе уравнение, получим

которое упрощается

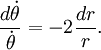
После интегрирования запишем выражение

для некоторой константы , которая является удельным угловым моментом ( ).Пусть

Уравнение движения в направлении становится равным

Закон всемирного тяготения Ньютона связывает силу на единицу массы с расстоянием как

где G — универсальная гравитационная константа и M — масса звезды.

В результате

Это дифференциальное уравнение имеет общее решение:

для произвольных констант интегрирования e и θ₀.

Заменяя u на 1/r и полагая θ₀ = 0, получим:

Мы получили уравнение конического сечения с эксцентриситетом e и началом системы координат в одном из фокусов. Таким образом, первый закон Кеплера прямо следует из закона всемирного тяготения Ньютона и второго закона Ньютона.