Инерциальная систем координат связанная с Землёй
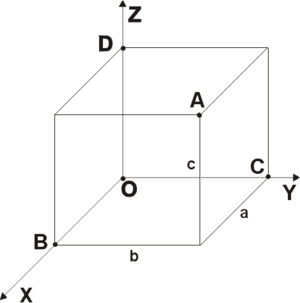
Рис. 1
Применение Земли в качестве ИСО, несмотря на приближённый его характер, широко распространено в навигации. Инерциальная система координат, как часть ИСО строится по следующему алгоритму. В качестве точки O- начала координат выбирается центр земли в соответствии с принятой её моделью. Ось z – совпадает с осью вращения земли. Оси x и y находятся в экваториальной плоскости. Следует заметить, что такая система не участвует во вращении Земли.
Галилей просто и ясно доказал связь между силой и изменением скорости (ускорением), а не между силой и самой скоростью, как считал Аристотель и его последователи. Это открытие Галилея вошло в науку как Закон инерции, который теперь также известен как первый закон Ньютона (1643—1727).
Классическая динамика основана на трёх основных законах Ньютона:
1-й: Существуют такие системы отсчета, относительно которых поступательно движущееся тело сохраняет свою скорость постоянной, если на него не действуют другие тела или их действие скомпенсировано.
Первый закон Ньютона утверждает, что существуют системы отсчета, в которых тела сохраняют состояние покоя или равномерного прямолинейного движения при отсутствии действий на них со стороны других тел или при взаимной компенсации этих воздействий.[8] Такие системы отсчета называются инерциальными. Ньютон предположил, что каждый массивный объект имеет определенный запас инерции, который характеризует «естественное состояние» движения этого объекта. Эта идея отрицает взгляд Аристотеля, который рассматривал покой «естественным состоянием» объекта. Первый закона Ньютона противоречит аристотелевской физике, одним из положений которой является утверждение о том, что тело может двигаться с постоянной скоростью лишь под действием силы. Тот факт, что в механике Ньютона покой физически неотличим от равномерного прямолинейного движения, является обоснованием принципа относительности Галилея. Среди совокупности тел принципиально невозможно определить какие из них находится «в движении», а какие «покоятся». Говорить о движении можно лишь относительно какой-либо системы отсчета. Законы механики выполняются одинаково во всех инерциальных системах отсчета, другими словами все они механически эквивалентны. Последнее следует из так называемых преобразований Галилея.[9]
Например, законы механики абсолютно одинаково выполняются в кузове грузовика, когда тот едет по прямому участку дороги с постоянной скорость и когда стоит на месте. Человек может подбросить мячик вертикально вверх и поймать его через некоторое время на том же самом месте вне зависимости от того движется ли грузовик равномерно и прямолинейно или покоится. Для него мячик летит по прямой. Однако для стороннего наблюдателя, находящегося на земле, траектория движения мячика имеет вид параболы. Это связано с тем, что мячик относительно земли движется во время полета не только вертикально, но и горизонтально по инерции в сторону движения грузовика. Для человека, находящегося в кузове грузовика не имеет значения движется ли последний по дороге, или окружающий мир перемещается с постоянной скоростью в противоположном направлении, а грузовик стоит на месте. Таким образом, состояние покоя и равномерного прямолинейного движения физически неотличимы друг от друга.
2-й: В инерциальной системе отсчета сумма всех сил, действующих на тело, равна произведению массы этого тела на векторное ускорение этого же тела (действие на тело силы, проявляется в сообщении ему ускорения).
В наиболее общем случае, который описывает также движение тела с изменяющейся массой (например, реактивное движение), 2-й закон Ньютона принято записывать следующим образом:
,
где
—
импульс
тела. Таким образом, сила характеризует
быстроту изменения импульса.
Хотя второй
закон Ньютона традиционно
записывают в виде:
,
сам Ньютон записывал его несколько
иначе, используя дифференциальное
исчисление.
Второй закон Ньютона в современной формулировке звучит так: в инерциальной системе отсчета скорость изменения импульса материальной точки равна векторной сумме всех сил, действующих на эту точку.
где
−
импульс материальной точки,
−
суммарная сила, действующая на материальную
точку. Второй закон Ньютона гласит, что
действие несбалансированных сил приводит
к изменению импульса материальной
точки.[8]
По определению импульса:
где
−
масса,
−
скорость.
По правилу нахождения производной произведения:
Если масса материальной точки остается неизменной, то производная по времени от массы равна нулю, и уравнение принимает вид:
Учитывая определение ускорения точки, второй закон Ньютона принимает вид:
Считается, что это «вторая самая известная формула в физике»[10], хотя сам Ньютон никогда явным образом не записывал свой второй закон в этом виде.
Поскольку в любой инерциальной системе отсчёта ускорение тела одинаково и не меняется при переходе от одной системы к другой, то и сила инвариантна по отношению к такому переходу.
Ма́сса (от греческого μάζα) — одна из важнейших физических величин. Первоначально (XVII—XIX века) она характеризовала «количество вещества» в физическом объекте, от которого, по представлениям того времени, зависели как способность объекта сопротивляться приложенной силе (инертность), так и гравитационные свойства — вес. В современной физике понятие «количество вещества» имеет другой смысл, а под массой понимают два различных свойства физического объекта:
Гравитационная масса показывает, с какой силой тело взаимодействует с внешними гравитационными полями (пассивная гравитационная масса) — фактически эта масса положена в основу измерения массы взвешиванием в современной метрологии, и какое гравитационное поле создаёт само это тело (активная гравитационная масса) — эта масса фигурирует в законе всемирного тяготения.
Инертная масса, которая характеризует меру инертности тел и фигурирует во втором законе Ньютона. Если произвольная сила в инерциальной системе отсчёта одинаково ускоряет разные исходно неподвижные тела, этим телам приписывают одинаковую инертную массу.
Гравитационная и инертная масса равны друг другу (практически с гигантской точностью (выше 10−15), а в большинстве физических теорий — точно), поэтому в большинстве случаев просто говорят о массе, не уточняя какую из них имеют в виду.
Масса тела не зависит от того, какие внешние силы на это тело действуют.